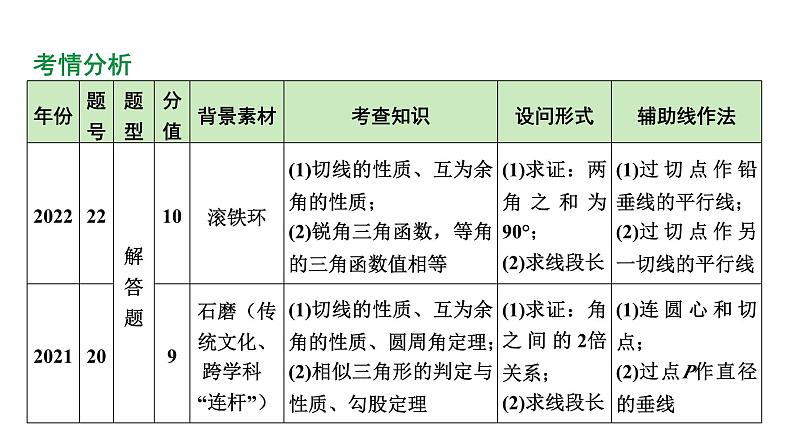
河南省2024年数学中考热点备考重难专题：真实情境中的圆问题（课件）

这是一份河南省2024年数学中考热点备考重难专题：真实情境中的圆问题（课件），共24页。PPT课件主要包含了课件说明，真实情境中的圆问题，课堂练兵，课后小练，典例精讲，考情分析，答题步骤，方法总结等内容，欢迎下载使用。

一、课件设计初衷 基于老师在总复习过程中对重难题型有较大的需求，以及纸质图书和板书展示二次函数图象与几何图形等重难点效果不佳而设计重难专题课件. 在制作过程中结合课件能使题图动态化且分步骤展示的特性，有助于学生题图结合梳理题意，理解平面图形的变化过程.二、课件亮点1.依据区域考情，针对性选题 按照本地区考情及考法选题，针对性强，有效提高老师备课效率2.贴近学生实际解题情境，形式符合教学习惯 审题时对题目数字、符号、辅助线、动图等关键信息进行题图批注，帮助学生梳理关键信息，激发学生兴趣，调动积极性3.含解题思路引导与方法总结，提高课堂互动性 通过问题启发式解题思路点拨，激发学生数学思考与探索. 方法总结使学生复习一类题，会一类题，取得有效的复习成果三、课件使用场景适用于中考专题复习或题位复习
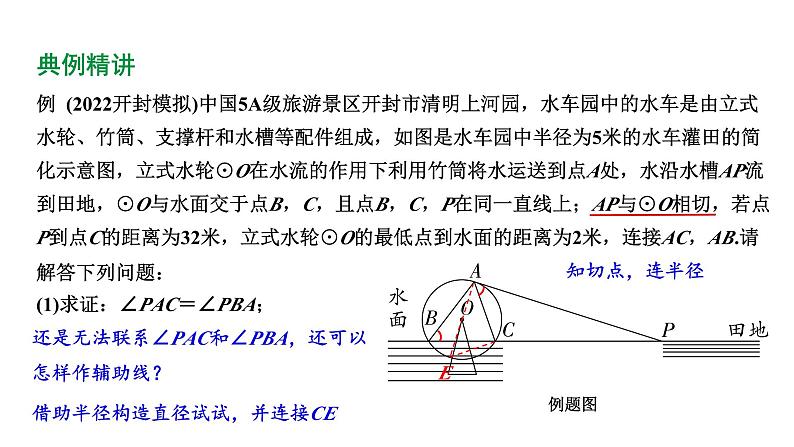
例 (2022开封模拟)中国5A级旅游景区开封市清明上河园，水车园中的水车是由立式水轮、竹筒、支撑杆和水槽等配件组成，如图是水车园中半径为5米的水车灌田的简化示意图，立式水轮⊙O在水流的作用下利用竹筒将水运送到点A处，水沿水槽AP流到田地，⊙O与水面交于点B，C，且点B，C，P在同一直线上；AP与⊙O相切，若点P到点C的距离为32米，立式水轮⊙O的最低点到水面的距离为2米，连接AC，AB.请解答下列问题：
(1)求证：∠PAC＝∠PBA；
还是无法联系∠PAC和∠PBA，还可以怎样作辅助线？
借助半径构造直径试试，并连接CE
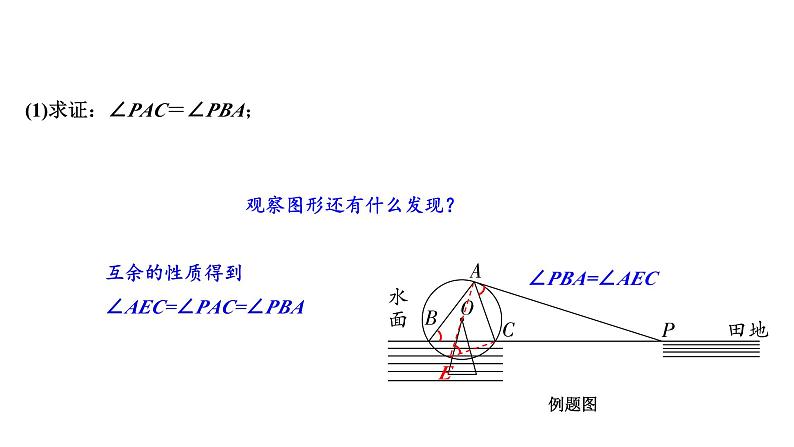
观察图形还有什么发现？
互余的性质得到∠AEC=∠PAC=∠PBA
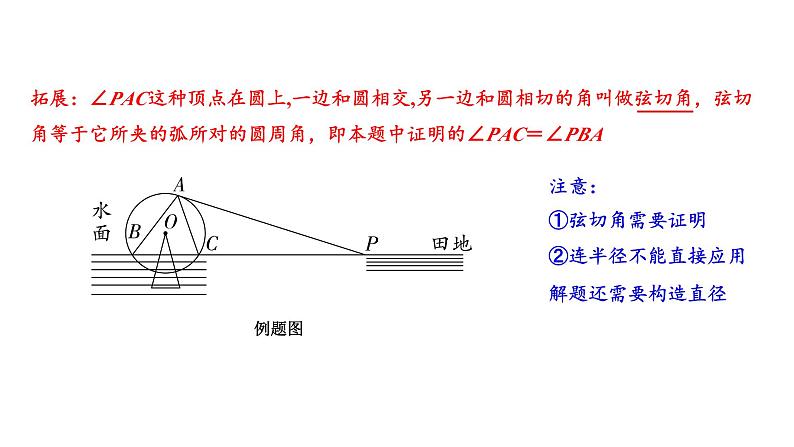
拓展：∠PAC这种顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角，弦切角等于它所夹的弧所对的圆周角，即本题中证明的∠PAC＝∠PBA
注意：①弦切角需要证明②连半径不能直接应用解题还需要构造直径
证得∠PAC＝∠PBA
(1)证明：如解图，连接AO并延长交⊙O于点E，连接CE，∵PA是⊙O的切线，∴∠EAP＝90°，∴∠EAC＋∠PAC＝90°，∵AE是⊙O的直径，∴∠ACE＝90°，∴∠EAC＋∠AEC＝90°，∴∠PAC＝∠AEC∵∠AEC＝∠ABC，∴∠ABC＝∠PAC，即∠PAC＝∠PBA；
(2)请求出水槽AP的长度．
求线段长我们可以想到什么方法？
图中构成A字型相似（有公共角，且另一组角相等）
Rt△OFC中求得FC，BC
切线的性质、圆周角定理及其推论、相似三角形的性质与判定、锐角三角函数、勾股定理
相似A字型，特点为有共用的一组角，且有另外一组角相等，形似字母“A”
辅助线作法：过圆心连半径，通常还要再转化构造直径去解题(题中没有给出直径的情况)
拓展：题中这种角是弦切角，弦切角等于它所夹的弧所对的圆周角
解题方法：1.证明角间数量关系切线的性质，圆周角定理的推论，两半径构成的等腰三角形，角间等量转换，两角互余的性质2.求线段长通常有3种方法：①锐角三角函数，此时线段要在直角三角形中或者能够构造直角三角形，用锐角三角函数需要已知一条边和一个角；②勾股定理，此时线段要在直角三角形中或者能够构造直角三角形，用勾股定理需要已知两边；③三角形相似、全等，用相似需要证明两组角相等，有等边则证明全等
练习 (2023河南原创卷)我国的纸伞工艺十分巧妙．如图①，伞不论张开还是缩拢，伞柄AP始终平分同一平面内两条伞骨所成的∠BAD，从而保证伞圈C能沿着伞柄滑动．小明受此启发设计了一个“简易平分角的仪器”，如图②，其中AB＝AD，BC＝DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们落在角的两边上，沿AC画一条射线AE，则AE为∠PRQ的平分线．
(1)如图②，试说明这个平分角的仪器的制作原理；
证得△ABC≌△ADC全等
(2)如图③，将上述平分角仪器的顶点A落在⊙O的直径MN的端点M处，边AB与直径MN共线，边AD与⊙O相交于点G，AC交⊙O于点E，过点E作⊙O的切线，与AD，BC分别交于点F，H.①求证：EF⊥AD；
连半径，得到OE⊥EF
能否证明AD∥OE，EF⊥AD？
内错角相等，两直线平行
(2)①证明：如图，连接OE，∵OE＝OA，∴∠OAE＝∠OEA，∵AC平分∠DAB；∴∠DAC＝∠BAC，∴∠DAC＝∠OEA，∴OE∥AD，∵FH是⊙O的切线，∴OE⊥EH，∴EF⊥AD；
②若⊙O半径为3，AE＝4，求FG的长．
放在哪个三角形中求解？
(2)如图③，将上述平分角仪器的顶点A落在⊙O的直径MN的端点M处，边AB与直径MN共线，边AD与⊙O相交于点G，AC交⊙O于点E，过点E作⊙O的切线，与AD，BC分别交于点F，H.
在Rt△ANE中，可得EN长
证明△EFG∽△AEN
练习1 人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也”．意思是说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．如下是弦切角定理一种情况的证明过程： 证明：如图①，∵AB与⊙O相切于点A, ∴∠CAB＝90°，∴弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．
为了验证这一定理的正确性，需要对其他情况进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出证明过程．已知：如图②，__________________，圆心O在∠BAC的内部，AD为⊙O的直径，点E为⊙O上一点，CE，AE为⊙O的弦．求证：______________．
练习2 (2022河南原创卷)与圆有关的定理，我们在初中阶段已经学习了很多，例如垂径定理，圆周角定理等．实际上，与圆相关的定理还有很多，如圆幂定理，它包含了相交弦定理，切割线定理，割线定理以及它们的推论，其中切割线定理的内容是：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．喜欢思考的天天在了解这个定理之后尝试给出证明，下面是他的部分证明过程：已知：如图①，点P为⊙O外一点，切线PA与⊙O相切于点A，割线PBC与⊙O相交于点B，C.求证：PA2＝PB·PC.证明：如图②，连接AB，AC，AO，BO，∵PA与⊙O相切于点A，∴PA⊥AO，即∠PAB＋∠BAO＝90°.…
(1)请你帮助天天将证明过程补充完整；
证明：如图②，连接AB，AC，AO，BO，∵PA与⊙O相切于点A，∴PA⊥AO，即∠PAB＋∠BAO＝90°.