2024年广东省中山市九年级中考三模数学试题

这是一份2024年广东省中山市九年级中考三模数学试题，文件包含2024年广东省中山市九年级中考三模数学试题docx、2024年中山市华侨中学初三数学第三次学情调研pdf等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。

1．如果+20%表示增加，那么-6%表示（ ）
A．减少B．减少C．增加D．增加
2．如图，下列四种通信标志中，其图案是轴对称图形的是（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．B．C．D．
4．如图，把一块三角板的直角顶点放在直线上，，，则（ ）
A．B．C．D．
5．在Rt中，，则的值为（ ）
A．B．C．D．
6．把抛物线向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（ ）
A．B．
C．D．
7．一组数据：3，4，4，4，5，下列对这组数据的统计量说法错误的是（ ）
A．平均数是4B．中位数是4C．方差是4D．众数是4
8．我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子去量竿，却比竿子短一托．”题目大意是：现有一根竿子和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短了5尺，设竿长为尺，绳索长为尺，则符合题意的方程组是（ ）
A．B．C．D
9．某几何体由若干个大小相同的小正方体组成，其主视图、左视图和俯视图都如图所示．则组成该几何体的小正方体的个数最少为（ ）
A．4个B．6个C．7个D．3个
10．如图，下面是三位同学的折纸示意图，则AD依次是的（ ）
A．中线、角平分线、高线B．高线、中线、角平分线
C．角平分线、中线、高线D．角平分线、高线、中线
二、填空题（本大题共5个小题，每小题3分，共15分）
11．16的平方根是______
12．若的值为整数，则的值可以为______．（写一个即可）
13．在中，，点是斜边的中点，若，，则的长度为______．
14．在一个不透明的袋子里装有2个红球和5个白球，它们除颜色外都相同，从中任意摸出1个球，则摸出的球为红球的概率为______．
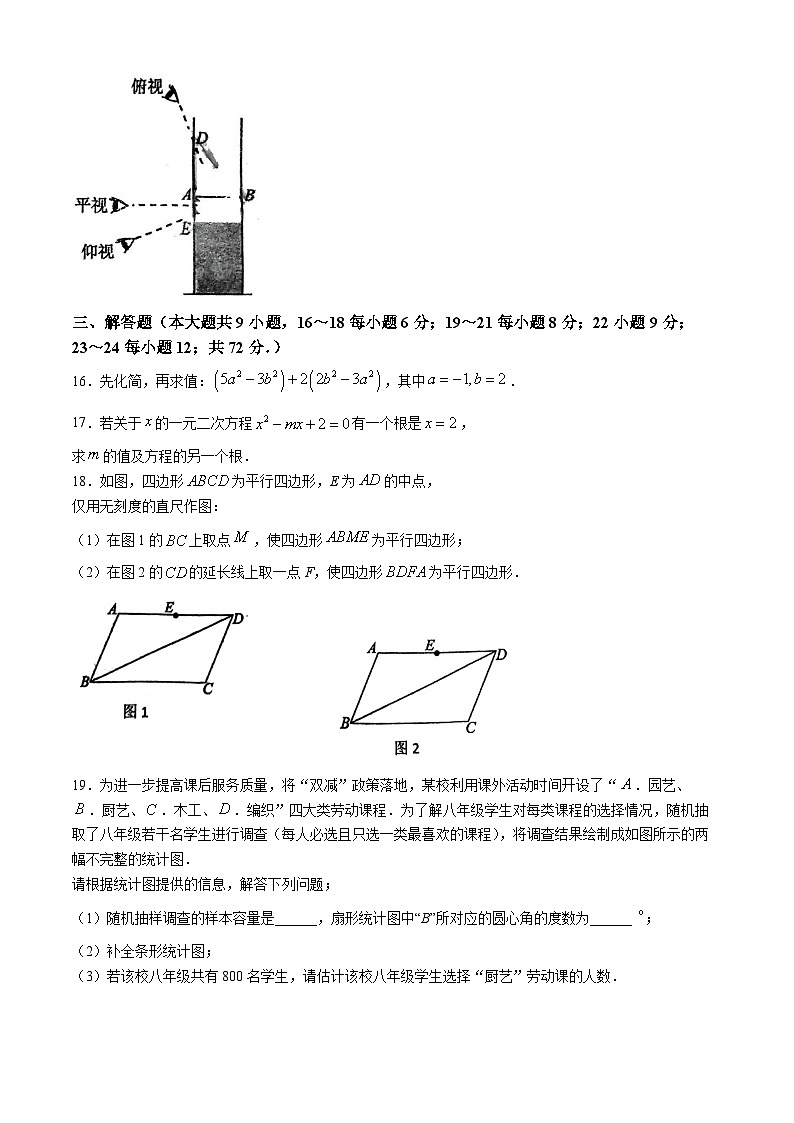
15．如图，量筒的液面呈凹形，近似看成圆弧，读数时视线要与液面相切于最低点C（即弧中点）．小温想探究仰视、俯视对读数的影响，当他俯视点C时，记录量筒上点D的高度为；仰视点C（点E、C、B在同一直线），记录量筒上点E的高度为，若点D在液面圆弧所在圆上，量筒直径为，则平视点C，点C的高度为______．
三、解答题（本大题共9小题，16～18每小题6分；19～21每小题8分；22小题9分；23～24每小题12；共72分．）
16．先化简，再求值：，其中．
17．若关于的一元二次方程有一个根是，
求的值及方程的另一个根．
18．如图，四边形为平行四边形，E为的中点，
仅用无刻度的直尺作图：
（1）在图1的上取点，使四边形为平行四边形；
（2）在图2的的延长线上取一点F，使四边形为平行四边形．
19．为进一步提高课后服务质量，将“双减”政策落地，某校利用课外活动时间开设了“．园艺、．厨艺、．木工、．编织”四大类劳动课程．为了解八年级学生对每类课程的选择情况，随机抽取了八年级若干名学生进行调查（每人必选且只选一类最喜欢的课程），将调查结果绘制成如图所示的两幅不完整的统计图．
请根据统计图提供的信息，解答下列问题；
（1）随机抽样调查的样本容量是______，扇形统计图中“B”所对应的圆心角的度数为______；
（2）补全条形统计图；
（3）若该校八年级共有800名学生，请估计该校八年级学生选择“厨艺”劳动课的人数．
20．随着电动车技术的日益发展和环保节能的优势，越来越多的购车者选择了新能源汽车，影响新能源汽车发展的重要瓶颈就是续航里程及充电时间．某公司用两种充电桩对目前电量为的新能源汽车充电．经测试，在用快速充电桩和普通充电桩对汽车充电时，其电量与充电时间（单位：）的函数图象分别为图2中的线段．根据以上信息，回答下列问题：
（1）求线段和线段所代表的函数解析式；（写出取值范围）
（2）在某次出行之前，李梅要对余电的电车充电，先用快速充电桩充电，再用普通充电桩充电，要求用2.5小时完成充电，请你设计一个合理的充电方案．
21．如图，是的直径，且，点是上的一个动点，是的一条弦，且
，点在的延长线上．
（1）若，求证：DE是的切线；
（2）若点C为半圆的中点，连接，求的长．
22．下面是一位同学的数学学习笔记，请仔细阅读并完成任务．
任务：（1）若，则当_____时，代数式取最小值，最小值为______；
（2）已知若，函数，试说明当取何值时，取得最小值，并求出的最小值；
（3）如图，已知点是反比例函数图象上一动点，点，则的面积的最小值为______．
23．如图，在边长为2的正方形中，E是边CD上一点（不与点C，D重合），连接，点D关于的对称点为F，连接并延长交边于点与相交于点．
（1）判断AE与DG的数量关系，并证明；
（2）当点F落在上时，求的长；
（3）当E为中点时，求的值．
24．在平面直角坐标系中，已知抛物线与轴分别交于点A、B（点A在点B的左侧），与轴交于点，其对称轴为直线．
（1）求该抛物线的表达式；
（2）点F是上述抛物线上位于第一象限的一个动点，直线分别与轴、线段交于点，过点F作轴于点N，交于点．
①当时，求点F的坐标；
②试判断四边形的形状，并证明．
数学课堂观测 参考答案
1．A2．C3．D4．C5．B6．B7．C8．B9．B10．D
11．12．4（答案不唯一）13．514．15．
16．解：原式
当时，
原式
17．解：设另一个根为，
解得，；
的值为3，方程的另一个根为1
18．
解：（1）如图，点即为所求．（2）如图，点即为所求．
19．（1）400,108；
（2）补全条形统计图如下：
（3）（名），
答：估计该校八年级学生选择“厨艺”劳动课的人数大约为240名．
20．解：（1）设线段解析式为，
把代入得：，
解得，
线段解析式为；
设线段解析式为，把代入得：
解得，
线段解析式为；
（2）设快速充电小时，则普通充电小时，
根据题意得：，
解得，
，
答：快速充电0.85小时，普通充电1.65小时．
21．（1）证：连接
为的直径
为的半径
是的切线
（2）连接，则
在中，
为半圆的中点
在RT中，
22．（1）26；
（2）
，当且仅当，即时，等号成立
即当时，函数函数取最小值，最小值为8．
（3）
23．
（1）
四边形是正方形
点关于对称
（2）
如备用图1，连接EF
四边形ABCD是边长为2的正方形，为其对角线
点关于对称，且点在上
（3）
如备用图2，延长交的延长线于点
在正方形中，
由（1）可知
为中点，
在RT中，，在RT中，
24．解：（1）由题意得：，
解得：，
则抛物线的表达式为：；
（2）如图过点作轴于点，则轴
由，得
设点
解得
（3）四边形为矩形
轴
∴即，且
即
四边形为矩形
当，即时，
时，矩形为正方形
用均值不等式求最值
若实数，则有，当且仅当时，取等号，我们称不等式为均值不等式．
证明：
由上可知，①当为定值的时候，有最大值；
②当为定值的时候，有最小值．
所以，利用均值不等式可以求一些函数的最值．
例：已知，求函数的最小值．
解：
，当且仅当，即时，等号成立
当即时，函数取最小值，最小值为2．
另略解：连接四点共圆
为中点，