2023-2024学年广西贵港市平南县八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年广西贵港市平南县八年级（下）期末数学试卷（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.“二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图，其中文字上面图案是中心对称图形的是( )
A. B. C. D.
2.下列几组数中，能作为直角三角形三边长的一组是( )
A. 6，8，12B. 0.1，0.2，0.3C. 3，4，5D. 2，3，5
3.在平面直角坐标系中，点A(4,−3)到y轴的距离为( )
A. 4B. −4C. 3D. −3
4.如图，在Rt△ABC中，CD是斜边AB上的中线，∠A=20°，则∠BCD的度数是( )
A. 40°B. 50°C. 60°D. 70°
5.过某个多边形一顶点的所有对角线，将这个多边形分成了5个三角形，则这个多边形是( )
A. 五边形B. 六边形C. 七边形D. 八边形
6.某班50名学生在一次数学测试中不及格人数的频率是0.1，则及格的同学有( )
A. 5位B. 40位C. 45位D. 30位
7.如图，在平行四边形ABCD中，AB=4，BC=6，对角线AC、BD相交于点O，则OA的取值范围是( )
A. 28.如图，为测量池塘边A、B两点的距离，小明在池塘的一侧选取一点O，测得OA、OB的中点分别是点D、E，且DE=14米，则A、B间的距离是( )
A. 18米B. 24米C. 28米D. 30米
9.如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点.连接AF，BF，∠AFB=90°，且AB=6，BC=10，则EF的长是( )
A. 2
B. 3
C. 4
D. 5
10.直线y=x+b上有三个点(−2.4,y1)，(−1.5,y2)，(1.3,y3).则y1，y2，y3的大小关系是( )
A. y1>y2>y3B. y1y1>y3
11.已知函数y=kx的图象如图所示，那么函数y=kx−k的图象大致是( )
A. B. C. D.
12.如图，在Rt△ABC中，∠BAC=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，则AM的最小值是( )
A. 43B. 65C. 34D. 56
二、填空题：本题共6小题，每小题2分，共12分。
13.一副三角板按如图方式摆放，且∠1比∠2大50°，则∠1=______°。
14.如图，一棵树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°夹角，这棵树在折断前的高度为______米．
15.若点P(−3a−4,2+a)在y轴上，则a= ______．
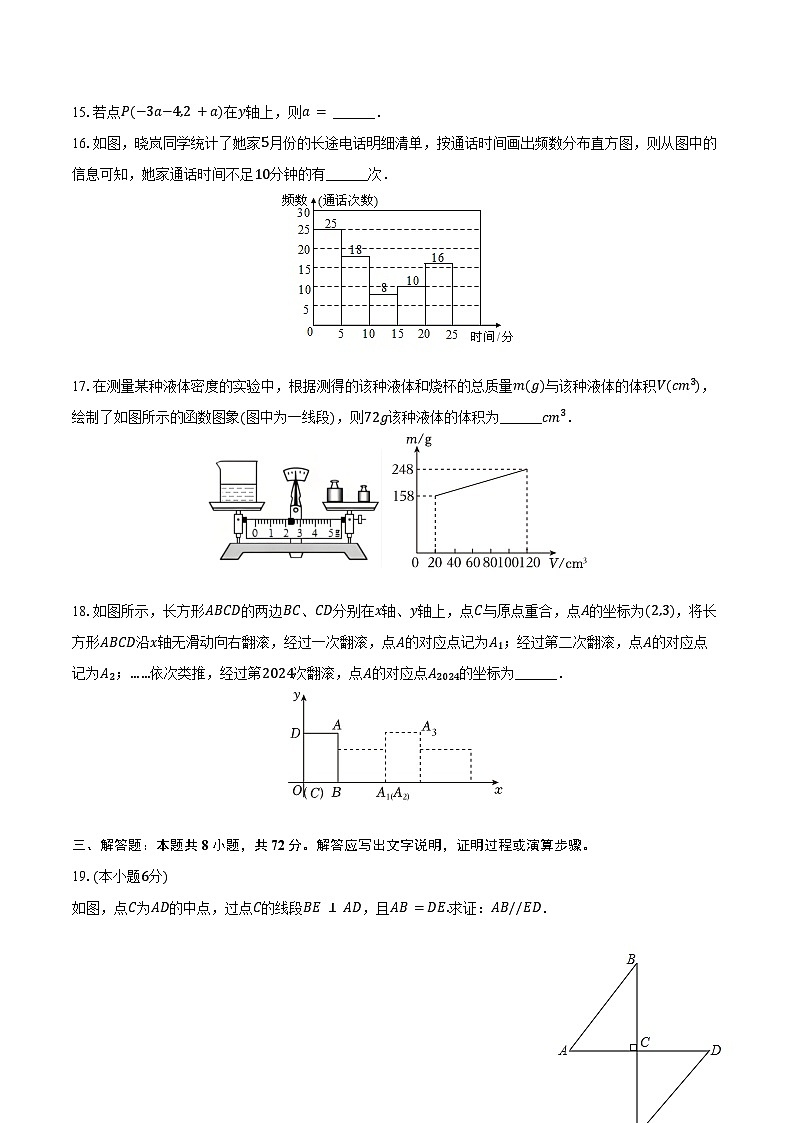
16.如图，晓岚同学统计了她家5月份的长途电话明细清单，按通话时间画出频数分布直方图，则从图中的信息可知，她家通话时间不足10分钟的有______次．
17.在测量某种液体密度的实验中，根据测得的该种液体和烧杯的总质量m(g)与该种液体的体积V(cm3)，绘制了如图所示的函数图象(图中为一线段)，则72g该种液体的体积为______cm3．
18.如图所示，长方形ABCD的两边BC、CD分别在x轴、y轴上，点C与原点重合，点A的坐标为(2,3)，将长方形ABCD沿x轴无滑动向右翻滚，经过一次翻滚，点A的对应点记为A1；经过第二次翻滚，点A的对应点记为A2；……依次类推，经过第2024次翻滚，点A的对应点A2024的坐标为______．
三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题6分)
如图，点C为AD的中点，过点C的线段BE⊥AD，且AB=DE.求证：AB//ED．
20.(本小题6分)
如图，车高4m(AC=4m)，货车卸货时后面支架AB弯折落在地面A1处，经过测量A1C=2m，求弯折点B与地面的距离．
21.(本小题10分)
作图题(不写作法)已知：如图，在平面直角坐标系中．
(1)作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标：A1(______)，B1(______)，C1(______)；
(2)直接写出△ABC的面积为______；
(3)在x轴上画点P，使|PA−PB|最大．
22.(本小题10分)
土壤的酸碱度由土壤中氢离子和氢氧根离子的相对浓度决定，通常采用pH来表示土壤的酸碱度.土壤的酸碱度对植物生长的“量”和“质”均有重要影响，某生物课题研究小组以“土壤酸碱度与小麦幼苗生长”为课题开展试验．
将若干株相同的小麦幼苗随机均分为9组，分别种植在pH值为4，4.5，5，5.5，6，6.5，7，7.5，8九个梯度的土壤中，经过40多天培育，观察后记录数据，整理并绘制了如下不完整的统计图表：
pH=6.5的土壤中小麦幼苗生长高度频数分布表
九个梯度的土壤中小麦幼苗生长的平均高度统计表
请根据以上图表信息，解答下列问题：
(1)补全频数分布直方图；
(2)若将小麦幼苗生长高度按A组每株30cm，B组每株31cm，C组每株32cm，D组每株33cm，E组每株34cm计算，则pH=6.5的土壤中小麦幼苗生长的平均高度约为多少？(结果精确到1cm)
(3)请根据试验数据写出一条合理的试验结论．
23.(本小题10分)
实践与探究题
问题：直角三角形除了三边之间、两个锐角之间有特殊的关系外，斜边上的中线有什么性质呢？
丽丽同学利用直角三角形纸片进行了如下的折叠实验：

(1)观察发现

①观察丽丽同学的折叠实验，你发现线段CD与AB之间有何数量关系？在图(1)所示的Rt△ABC中，∠C=90°，CD是斜边AB上中线.请根据图(1)证明你的猜想．
②根据上面的探究，总结直角三角形斜边上的中线性质．
(2)拓展应用：如图(2)，CD是Rt△ABC的斜边AB上的高，若CD=5，则Rt△ABC面积的最小值等于______．
24.(本小题10分)
如图，在平面直角坐标系xOy中，直线l1：y=kx−1与直线l2：y=12x+2交于点A(m,1)．
(1)求m的值和直线l1的表达式；
(2)设直线l1，l2分别与y轴交于点B，C，求△ABC的面积；
(3)结合图象，直接写出不等式025.(本小题10分)
2024年4月18日上午10时08分，华为Pura70系列正式开售，华为Pura70Ultra和Pura70Pr已在华为商城销售，约一分钟即告售罄.“4G改变生活，5G改变社会”，不一样的5G手机给人们带来了全新的体验，某营业厅现有A、B两种型号的5G手机出售，售出1部A型、1部B型手机共获利600元，售出3部A型、2部B型手机共获利1400元．
(1)求A、B两种型号的手机每部利润各是多少元；
(2)某营业厅再次购进A、B两种型号手机共20部，其中B型手机的数量不超过A型手机数量的23，请设计一个购买方案，使营业厅销售完这20部手机能获得最大利润，并求出最大利润．
26.(本小题10分)
在正方形ABCD中，E是边AD上的一动点(不与点A，D重合)，连接BE，点C关于直线BE的对称点为F，连接FA，FB．
(1)如图1，若△ABF是等边三角形，则∠ABE= ______°；
(2)如图2，延长BE交FA的延长线于点M，连接CF交BE于点H，连接DM．
①求∠MFH的大小；
②用等式表示线段MB，MD，AB之间的数量关系，并证明．
参考答案
1.D
2.C
3.A
4.D
5.C
6.C
7.B
8.C
9.A
10.B
11.C
12.B
13.70
14.12
15.−43
16.43
17.80
18.(5062,3)
19.证明：∵点C为AD的中点，
∴AC=CD，
∵BE⊥AD，
∴∠ACB=∠DCE=90°，
在Rt△ACB和Rt△DCE中，
AB=DEAC=DC，
∴Rt△ACB≌Rt△DCE(HL)，
∴∠A=∠D，
∴AB//ED．
20.解：由题意得，AB=A1B，∠BCA1=90°，
设BC=xm，则AB=A1B=(4−x)m，
在Rt△A1BC中，A1C2+BC2=A1B2，
即：22+x2=(4−x)2，
解得：x=32，
答：弯折点B与地面的距离为32米．
21.−1，2 −3，1 −4，3 52
【解析】解：(1)如图所示，
由图可知，A1(−1,2)，B1(−3,1)，C1(−4,3)；
故答案为：−1，2；−3，1；−4，3；
(2)52；
(3)如图，点P即为所求点．
22.解：(1)总数有12÷0.1250=96(株)，
B组有96×0.2500=24(株)，
D组有96−12−24−36−6=18(株)，
补全频数分布直方图如下：

(2)32cm，
答：pH=6.5的土壤中小麦幼苗生长的平均高度约为32cm；
(3)土壤pH值在6～7.5时，小麦幼苗的长势较好；无论土壤pH过大还是过小，对小麦幼苗的生长高度都有很大的影响等．(答案不唯一，合理即可)．
23.解：(1)①由折叠知：CD=BD=AD=12AB，证明如下：
图中，倍长CD至点E得CD=DE，连接BE，
在△BDE和△ADC中，
BD=AD∠BDE=∠ADCCD=DE，
∴△CDA≌△EDB，
∴∠DCA=∠DEB，BE=AC，
∵∠DCA+∠BCE=90°，
∴∠BCE+∠BEC=90°，
∴∠EBC=∠BCA=90°，
在△BCA和△CBE中，
BE=CA∠EBC=∠BCABC=CB，
∴△ACB≌△EBC，
∴CE=AB，
∴CD=12AB；
②直角三角形斜边上的中线等于斜边的一半；
(2)25．
24.解：(1)把A(m,1)代入y=12x+2得12m+2=1，解得m=−2，
∴A(−2,1)，
把A(−2,1)代入y=kx−1得−2k−1=1，解得k=−1，
∴直线l1的表达式为y=−x−1；
(2)当x=0时，y=12x+2=2，则C(0,2)；
当x=0时，y=−x−1=−1，则B(0,−1)，
∴△ABC的面积=12×(2+1)×2=3；
(3)当y=0时，−x−1=0，解得x=−1，
∴直线y=−x−1与x轴的交点坐标为(−1,0)，
当−2即不等式025.解：(1)设A种型号手机每部利润是a元，B种型号手机每部利润是b元，
根据题意得：a+b=6003a+2b=1400，
解得：a=200b=400．
答：A种型号手机每部利润是200元，B种型号手机每部利润是400元；
(2)设购进A种型号的手机x部，获得的利润为w元，则购进B种型号的手机(20−x)部，
根据题意得：w=200x+400(20−x)，
即w=−200x+8000，
∵B型手机的数量不超过A型手机数量的23，
∴20−x≤23x，
解得：x≥12，
∵k=−200<0，
∴w随x的增大而减小，
∴当x=12时，w取得最大值，最大值为−200×12+8000=5600(元)，此时20−x=20−12=8(部)．
答：营业厅购进A种型号手机12部，B种型号手机8部时能获得最大利润，最大利润是5600元．
26.(1)15°．
(2)①如图，
∵四边形ABCD是正方形，
∴∠ABC=90°，BA=BC，
∵点F与点C关于直线BE对称，
∴BF=BC，∠MHF=90°，
∴BF=BA，
设∠1=α，
在△BFC中，BF=BC，
∴∠2=180°−(90°+α)2=45°−α2，
在△BFA中，BF=BA，
∴∠BFA=180°−∠12=90°−α2．
∴∠3=∠BFA−∠2=(90°−α2)−(45°−α2)=45°．
②数量关系：MB2+MD2=2AB2，证明如下：
过点A作AN⊥AM交BM于点N，连接BD，如图，
在Rt△FHM中，∠3=45°，
∴∠HMF=45°，
∴∠ANM=∠AMN=45°，∠ANB=135°，
∴AM=AN，
∵四边形ABCD是正方形，
∴∠BAD=90°，AD=AB，BD= 2AB，
∴∠4=∠5，
∴△AMD≌△ANB(SAS)，
∴∠AMD=∠ANB=135°，
∴∠BMD=∠AMD−∠AMN=90°，
在Rt△BMD中，由勾股定理得MB2+MD2=BD2，
即MB2+MD2=2AB2．
组别
小麦高度/cm
频数
频率
A
29.5～30.5
12
0.1250
B
30.5～31.5
0.2500
C
31.5～32.5
36
0.3750
D
32.5～33.5
E
33.5～34.5
6
0.0625
土壤酸碱度pH值
4
4.5
5
5.5
6
6.5
7
7.5
8
小麦幼苗生长平均高度/cm
22
24
27
28
30
29
30
25