2023-2024学年广西南宁三中高一（下）期末数学试卷（含解析）

这是一份2023-2024学年广西南宁三中高一（下）期末数学试卷（含解析），共14页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.若复数z=(3−4i)i，则z的虚部为( )
A. 3iB. 3C. 4iD. 4
2.某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件，为检验产品的质量，现用按比例分层随机抽样的方法从以上所有的产品中抽取60件进行检验，则应从乙种型号的产品中抽取件数为( )
A. 24B. 9C. 36D. 18
3.四名同学各掷骰子5次，分别记录每次骰子出现的点数，根据四名同学的统计结果，可以判断出一定没有出现点数6的是( )
A. 平均数为3，中位数为2B. 中位数为3，众数为2
C. 平均数为2，方差为2.4D. 中位数为3，方差为2.8
4.已知在平行四边形ABCD中，E为AC上靠近点A的三等分点，设BA=a,BC=b，则BE=( )
A. 23a−+13b−B. 13a+23bC. 512a−12bD. 43a−13b
5.已知圆锥的底面半径为 2，其侧面展开图为一个半圆，则该圆锥的体积为( )
A. 63πB. 2 63πC. 4 63πD. 8 63π
6.已知向量m=(2,λ)，n=(2−λ,−4)，若m与n共线且反向，则实数λ的值为( )
A. 4B. 2C. −2D. −2或4
7.在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑.在鳖臑P−ABC中，PA⊥平面ABC，AC⊥CB，PA=2BC=2，AC= 3，则此四面体的外接球表面积为( )
A. 3πB. 8πC. 9πD. 8 23π
8.有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回地随机取两次，每次取1个球.甲表示事件“第一次取出的球的数字是4”，乙表示事件“第二次取出的球的数字是5”，丙表示事件“两次取出的球的数字之和是6”，丁表示事件“两次取出的球的数字之和是7”，则( )
A. 甲与乙互斥B. 丙发生的概率为16C. 甲与丁相互独立D. 乙与丙相互独立
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。
9.在△ABC中，角A，B，C所对的边分别为a，b，c，下列说法中正确的是( )
A. 若bcsC+ccsB=b，则△ABC是等腰三角形
B. 若B=30°,b=2,c=2 2，则C=45°
C. 若a=2,b=4,csC=14，则c=4
D. 若△ABC面积为S=14(a2+b2−c2)，则C=45°
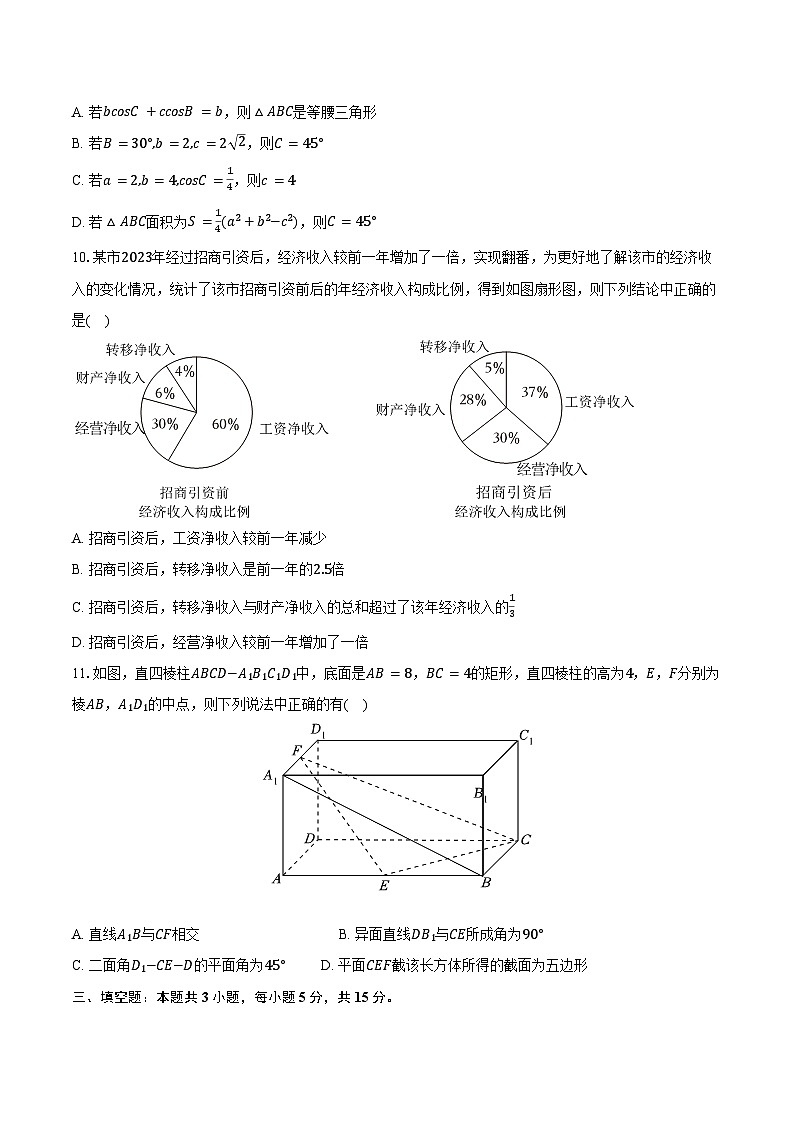
10.某市2023年经过招商引资后，经济收入较前一年增加了一倍，实现翻番，为更好地了解该市的经济收入的变化情况，统计了该市招商引资前后的年经济收入构成比例，得到如图扇形图，则下列结论中正确的是( )
A. 招商引资后，工资净收入较前一年减少
B. 招商引资后，转移净收入是前一年的2.5倍
C. 招商引资后，转移净收入与财产净收入的总和超过了该年经济收入的13
D. 招商引资后，经营净收入较前一年增加了一倍
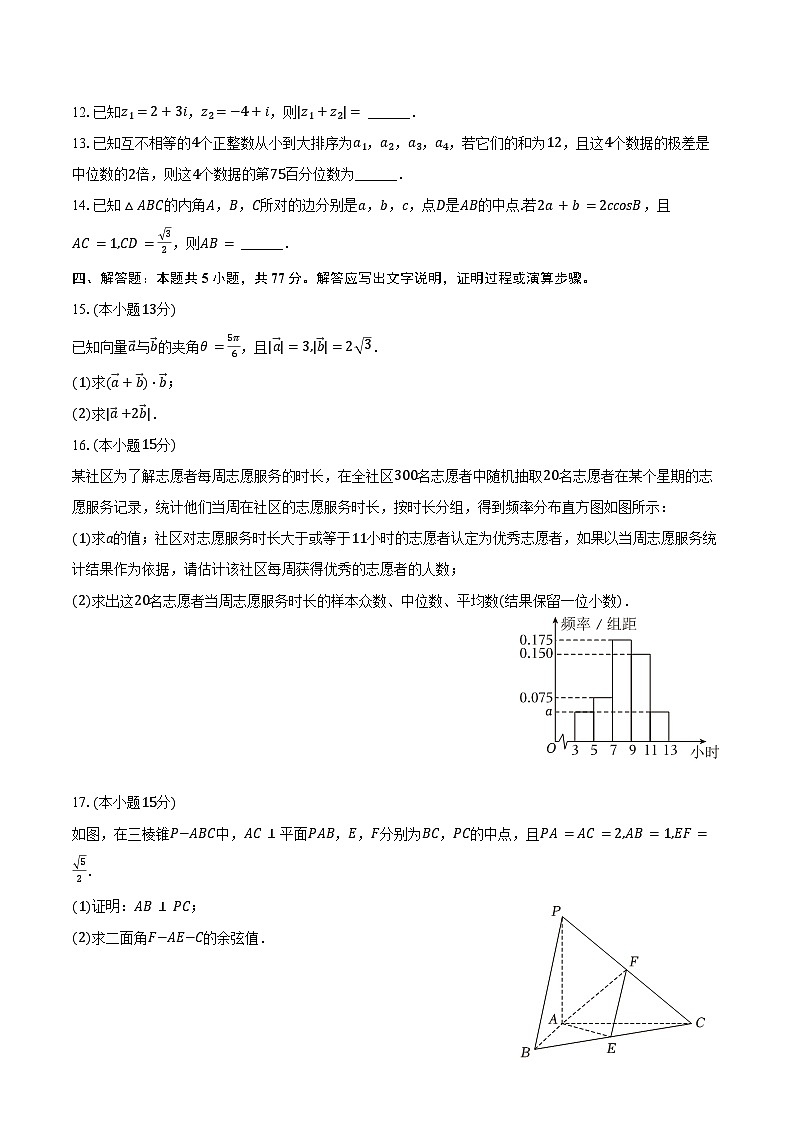
11.如图，直四棱柱ABCD−A1B1C1D1中，底面是AB=8，BC=4的矩形，直四棱柱的高为4，E，F分别为棱AB，A1D1的中点，则下列说法中正确的有( )
A. 直线A1B与CF相交 B. 异面直线DB1与CE所成角为90°
C. 二面角D1−CE−D的平面角为45° D. 平面CEF截该长方体所得的截面为五边形
三、填空题：本题共3小题，每小题5分，共15分。
12.已知z1=2+3i，z2=−4+i，则|z1+z2|= ______．
13.已知互不相等的4个正整数从小到大排序为a1，a2，a3，a4，若它们的和为12，且这4个数据的极差是中位数的2倍，则这4个数据的第75百分位数为______．
14.已知△ABC的内角A，B，C所对的边分别是a，b，c，点D是AB的中点.若2a+b=2ccsB，且AC=1,CD= 32，则AB= ______．
四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题13分)
已知向量a与b的夹角θ=5π6，且|a|=3,|b|=2 3．
(1)求(a+b)⋅b；
(2)求|a+2b|．
16.(本小题15分)
某社区为了解志愿者每周志愿服务的时长，在全社区300名志愿者中随机抽取20名志愿者在某个星期的志愿服务记录，统计他们当周在社区的志愿服务时长，按时长分组，得到频率分布直方图如图所示：
(1)求a的值；社区对志愿服务时长大于或等于11小时的志愿者认定为优秀志愿者，如果以当周志愿服务统计结果作为依据，请估计该社区每周获得优秀的志愿者的人数；
(2)求出这20名志愿者当周志愿服务时长的样本众数、中位数、平均数(结果保留一位小数)．
17.(本小题15分)
如图，在三棱锥P−ABC中，AC⊥平面PAB，E，F分别为BC，PC的中点，且PA=AC=2,AB=1,EF= 52．
(1)证明：AB⊥PC；
(2)求二面角F−AE−C的余弦值．
18.(本小题17分)
如图，在平面四边形ABCD中，AD= 3，CD=1，∠ACD=60°，∠ABC=30°．
(1)证明：AD⊥CD；
(2)求△ABC面积的最大值；
(3)设E为线段AB的中点，求DE的最大值．
19.(本小题17分)
在某抽奖活动中，初始时的袋子中有3个除颜色外其余都相同的小球，颜色为2白1红.每次随机抽取一个小球后放回.抽奖规则如下：设定抽中红球为中奖，抽中白球为未中奖；若抽到白球，放回后把袋中的一个白色小球替换为红色；若抽到红球，放回后把三个球的颜色重新变为2白1红的初始状态.记第n次抽奖中奖的概率为Pn．
(1)求P2，P3；
(2)若存在实数a，b，c，对任意的不小于4的正整数n，都有Pn=aPn−1+bPn−2+cPn−3，试确定a，b，c的值，并证明上述递推公式；
(3)若累计中奖4次及以上可以获得一枚优胜者勋章，则从初始状态下连抽9次获得至少一枚勋章的概率为多少？
答案解析
1.B
【解析】解：z=(3−4i)i=4+3i，
故其虚部为3，
故选：B．
2.A
【解析】解：用按比例分层随机抽样的方法从以上所有的产品中抽取60件进行检验，
则应从乙种型号的产品中抽取件数为：60×400200+400+300+100=24．
故选：A．
3.C
【解析】解：对于A，当投掷骰子出现结果为1，1，2，5，6时，满足平均数为3，中位数为2，可以出现点数6，故A错误；
对于B，当投掷骰子出现结果为2，2，3，4，6时，满足中位数为3，众数为2，可以出现点数6，故B错误；
对于C，若平均数为2，且出现6点，则方差S2>15(6−2)2=3.2>2.4，
∴平均数为2，方差为2.4时，一定没有出现点数6，故C正确；
对于D，当投掷骰子出现结果为1，2，3，3，6时，满足中位数为3，
平均数为：x−=15(1+2+3+3+6)=3
方差为S2=15[(1−3)2+(2−3)2+(3−3)2+(3−3)2+(6−3)2]=2.8，可以出现点数6，故D错误．
故选：C．
4.A
【解析】解：因为平行四边形ABCD中，E为AC上靠近点A的三等分点，
所以AE=13AC，
所以BE=AE−AB=13AC−AB=BA+13AC=BA+13(BC−BA)=23BA+13BC=23a+13b．
故选：A．
5.B
【解析】解：设圆锥母线长为l，高为ℎ，底面半径为r= 2，
则由2π× 2=πl，得l=2 2，
所以ℎ= l2−r2= 6，
所以V=13πr2ℎ=13π× 2× 6=2 63π．
故选：B．
6.A
【解析】解：由向量m=(2,λ)，n=(2−λ,−4)共线，得λ(2−λ)=−8，解得λ=−2或λ=4，
当λ=−2时，m=(2,−2)，n=(4,−4)，m与n同向，不符合题意，
当λ=4时，m=(2,4)，n=(−2,−4)，m与n反向，符合题意，
所以实数λ的值为4．
故选：A．
7.B
【解析】解：∵PA⊥平面ABC，∴PA⊥AB，PA⊥BC，又AC⊥CB，
∴可得BC⊥平面PAC，∴BC⊥PC，
∴此四面体的外接球的球心即为PB的中点，直径即为PB，
设球的半径为R，
∵PA=2BC=2，AC= 3，∴AB=2，
∴2R=PB= PA2+AB2= 22+22=2 2，∴R= 2，
∴此四面体的外接球表面积为4πR2=8π．
故答案为：B．
8.C
【解析】解：由题意可知，有放回地随机取两次，共有36种情况，
两点数和为6的所有可能为(1,5)，(2,4)，(3,3)，(4,2)，(5,1)，共5种情况，
两点数和为7的所有可能为(1,6)，(2,5)，(3,4)，(4,3)，(5,2)，(6,1)，共6种情况，
所以P(丙)=536，P(丁)=636=16，
P(甲)=16，P(乙)=16，P(丙)=56×6=536，P(丁)=66×6=16，
对于A选项，甲与乙可以同时发生，故选项 A错误；
对于B选项，P(丙)=536，故选项B错误；
对于C选项，P(甲丁)=136，P(甲)=16，P(丁)=16，
所以P(甲丁)=P(甲)P(丁)，即甲与丁相互独立，故选项C正确；
对于D选项，P(乙丙)=136，P(乙)=16，P(丙)=536，
所以P(乙丙)≠P (乙)P (丙)，即乙与丙不独立，故选项D错误．
故选：C．
9.ACD
【解析】解：选项A，由正弦定理及bcsC+ccsB=b，得sinBcsC+sinCcsB=sinB，
所以sin(B+C)=sinA=sinB，
因为A，B∈(0,π)，所以A=B，
所以△ABC是等腰三角形，即选项A正确；
选项B，由正弦定理知，bsinB=csinC，
所以sinC=csinBb=2 2×122= 22，
因为b选项C，由余弦定理知，c2=a2+b2−2abcsC=4+16−2×2×4×14=16，
所以c=4，即选项C正确；
选项D，因为S=14(a2+b2−c2)=12absinC，
所以a2+b2−c2=2absinC，
由余弦定理知，a2+b2−c2=2abcsC，
所以sinC=csC，即tanC=1，
又0°故选：ACD．
10.BD
【解析】解：设招商引资前经济收入为M，而招商引资后经济收入为2M，
对于A，招商引资前工资性收入为M×60%=0.6M，而招商引资后的工资性收入为2M×37%=0.74M，
所以工资净收入增加了，故A错误；
对于B，招商引资前转移净收入为M×4%=0.04M，招商引资后转移净收入为2M×5%=0.1M，
所以招商引资后，转移净收入是前一年的2.5倍，故B正确；
对于C，招商引资后，转移净收入与财产净收入的总和为0.1M+0.56M=0.66M<13×2M，
所以招商引资后，转移净收入与财产净收入的总和低于该年经济收入的13，故C错误；
对于D，招商引资前经营净收入为M×30%=0.3M，招商引资后经营净收入为2M×30%=0.6M，
所以招商引资后，经营净收入较前一年增加了一倍，故D正确．
故选：BD．
11.AD
【解析】解：因为A1F//BC且AF≠BC，可得四边形CFA1B为梯形，
所以CF与BA1必相交，所以A正确；
由题意，在长方体ABCD−A1B1C1D1中，因为BB1⊥平面ABCD，
CE⊂平面ABCD，所以BB1⊥CE，
假设异面直线DB1与CE所成角是90°，即DB1⊥CE．
DB1BB1⊂平面BB1D，DB1∩BB1=B1．
可得CE⊥平面BB1D，而DB⊂平面BB1D，
则CE⊥DB，
在长方形ABCD中，因为AB=8，BC=4，
取CD中点F，可知正方形BCFE中CE⊥BF，
可得DB与CE不垂直，矛盾，
所以异面直线DB1与CE所成角不是90°，所以B错误；
由上图可知DE=CE=4 2，又CD=8，即CD2=CE2+DE2，则CE⊥DE，
又DD1⊥平面ABCD，CE⊂平面ABCD，所以CE⊥DD1，
DD1∩DE=D，DD1，DE⊂平面DD1E所以CE⊥平面DD1E，
D1E⊂平面DD1E，则CE⊥D1E，则∠DED1为二面角D1−CE−D的平面角，
又tan∠DED1=DD1DE=44 2= 22，所以∠DED1不等于45°，C错误；
点P是棱C1D1上一点，且D1P=2，取C1D1的中点M，连接A1M，MC，PF，
因为F，P分别是A1D1和D1C1的中点，所以PF//A1M.
由四边形A1MCE为平行四边形，所以PF/​/CE，
因为平面ABCD//平面A1B1C1D1所以PF为平面CEF与平面A1B1C1D1的交线，
PF，PC，CE为截面的边，截面又与平面ABB1A1及ADD1A1相交，
可得截面的两条边，所以截面共有五边形，所以D正确．
故选：AD．
12.2 5
【解析】解：z1=2+3i，z2=−4+i，则|z1+z2|=|2+3i−4+i|=|−2+4i|= (−2)2+42=2 5．
故答案为：2 5．
13.92
【解析】解：互不相等的4个正整数从小到大排序为a1，a2，a3，a4，
则这4个数据的极差为：a4−a1，中位数为a2+a32，
这4个数据的极差是中位数的2倍，
则a4−a1=2×a2+a32=a2+a3，即a4=a1+a2+a3，
a1，a2，a3，a4的和为12，
则a1+a2+a3+a4=12，
故a4=6，
a1，a2，a3从小到大且为互不相等的正实数，
则a1=1，a2=2，a3=3，
4×0.75=3，
则这4个数据的第75百分位数为3+62=92．
故答案为：92．
14. 7
【解析】解：因为2a+b=2ccsB，由正弦定理得2sinA+sinB=2sinCcsB，
又因为sinA=sin(B+C)=sinBcsC+csBsinC，
所以2sinBcsC+sinB=0，
因为B∈(0,π)，可得sinB>0，所以csC=−12，
又因为CD为△ABC的一条中线，CD= 32，
可得CD=12(CA+CB)，
所以CD2=14(CA2+CB2+2CA⋅CB)，
即34=14[1+a2+2×1×a×(−12)]，解得a=2或a=−1(舍)．
由余弦定理得AB=c= a2+b2−2abcsC= 22+12−2×1×2×(−12)= 7．
故答案为： 7．
15.解：因为a与b的夹角θ=5π6，且|a|=3,|b|=2 3，
所以a⋅b=|a||b|csθ=3×2 3×(− 32)=−9，
所以(a+b)⋅b=a⋅b+b2=−9+12=3；
(2)|a+2b|′= (a+2b)2= a2+4a⋅b+4b2= 9+4×(−9)+4×12= 21．
【解析】(1)由平面向量的数量积运算即可求得；
(2)由求模公式计算即可求得．
16.解：(1)根据题意可得(a+0.075+0.175+0.15+a)×2=1，
∴a=0.05；
∵服务时长大于或等于11小时的频率为0.05×2=0.1，
∴估计该社区每周获得优秀的志愿者的人数为300×0.1=30；
(2)这20名志愿者当周志愿服务时长的样本众数为8小时；
中位数为7+0.5−0.1−≈8.4小时；
平均数为4×0.1+6×0.15+8×0.35+10×0.3+12×0.1=8.3小时．
【解析】(1)根据频率分布直方图的性质，即可求解；
(2)根据众数的概念，中位数的概念，平均数的概念，即可求解．
17.解：(1)证明：∵E，F分别为BC，PC的中点，
∴PB=2EF= 5，
∵AB2+PA2=PB2，∴AB⊥PA，∵AC⊥平面PAB，
∴AB⊥AC，
∵AC∩PA=A，AC，PA⊂平面PAC，
∴AB⊥平面PAC，PC⊂平面PAC，
∴AB⊥PC；
(2)根据题意，取AC的中点M，过M作MN⊥AE交AE于N，
连接FM，FN，ME，
因为F为PC中点，M为AC的中点，
则FM////PA，且FM=12PA=1，
又PA⊥AB，PA⊥AC，AB∩AC=A，AB，AC⊂平面ABC，
∴PA⊥平面ABC，
∴FM⊥平面ABC，而AE⊂平面ABC，
∴AE⊥FM，又MN⊥AE，FM∩MN=M，FM，MN⊂平面FMN，
∴AE⊥平面FMN，
∵FN⊂平面FMN，∴AE⊥FN，
即∠FNM为二面角F−AE−C的平面角，
在Rt△AME中，AM=1，ME=12，则AE= 1+14= 52，
由等面积可得MN=AM⋅MEAE=1×12 52= 55，
∴tan∠FNM=FMNM=1 55= 5，
则cs∠FNM= 66，即二面角F−AE−C的余弦值为 66．
【解析】(1)先根据勾股定理逆定理证得AB⊥PA，再根据AB⊥AC，即可证出；
(2)取AC的中点M，过M作MN⊥AE交AE于N，连接FM、FN，ME，由几何关系证明∠FNM为二面角F−AE−C的平面角，再由勾股定理和等面积求出MN即可求出结果．
18.解：(1)由题知，在△ACD中，
由正弦定理得sin∠CADCD=sin∠ACDAD，∴sin∠ACD=12，
∵AD>CD，∴∠ACD>∠CAD，∴∠CAD=π6，
∴∠D=π−∠ACD−∠CAD=π2，∴AD⊥CD；
(2)在△ABC中，根据勾股定理可得AC=2，
由余弦定理知：cs∠ABC=AB2+BC2−AC22AB⋅BC= 32
∴AB2+BC2=4+ 3AB⋅BC，∵AB2+BC2≥2AB⋅BC，∴2AB⋅BC≤4+ 3AB⋅BC
解得：AB⋅BC≤42− 3=8+4 3，当且仅当AB=BC时取等号，
∴S△ABC=12AB⋅BC⋅sinB≤2+ 3；
(3)在△ABC中，设∠BAC=θ∈(0,5π6)，由正弦定理知：ABsin∠ACB=ACsin∠B，
∴AB=4sin(5π6−θ),AE=2sin(5π6−θ)，
在△ADE中，由余弦定理知：DE2=AD2+AE2−2AD⋅AEcs∠DAE，
∴DE2=3+4sin2(5π6−θ)−4 3sin(5π6−θ)cs(π6+θ)
=3+4sin2(π6+θ)−4 3sin(π6+θ)cs(π6+θ)
=3+2[1−cs(π3+2θ)]−4 3sin(π6+θ)cs(π6+θ)
=5−2cs(π3+2θ)−2 3sin(π3+2θ)=5−4sin(π3+2θ+π6)
=5−4sin(π2+2θ)=5−4cs2θ∈(1,9],
∴DE2≤9，当仅当∠BAC=π2时取等号，∴DE的最大值等于3．
【解析】(1)根据正弦定理，可得∠D=π2；(2)根据余弦定理，不等式可得AB⋅BC的最值，从而得面积的最值；(3)根据余弦定理，正弦定理，辅助角公式可得DE的最值．
19.解：(1)P2=13×13+23×23=59，
P3=P2×13+23×13×1+13×23×23=59；
(2)因为每次中奖后袋中的球会回到初始状态，
从初始状态开始，若第一次中奖，此时第n次抽奖中奖的概率为13Pn−1，
从初始状态开始，若第一次未中奖而第二次中奖，此时第n次抽奖中奖的概率为23×23×Pn−2=49Pn−2，
从初始状态开始，若前两次均未中奖，则第三次必中奖，
此时第n次抽奖中奖的概率为23×13×1×Pn−3=29Pn−3，
综上所述，对任意的n≥4，Pn=13Pn−1+49Pn−2+29Pn−3，
又Pn=aPn−1+bPn−2+cPn−3，
所以a=13,b=49,c=29；
(3)由题意知每抽三次至少有一次中奖，
故连抽9次至少中奖3次，
所以只需排除3次中奖的情况即可获得一枚优胜者勋章，
另外，每两次中奖的间隔不能超过三次，每次中奖后袋中的球会回到初始状态，
从初始状态开始，抽一次中奖的概率为Q1=13，
从初始状态开始抽两次，第一次未中奖而第二次中奖的概率为Q2=49，
从初始状态开始抽三次，前两次均未中奖而第三次中奖的概率为Q3=29，
用(i,j,k)表示第i次，第j次，第k次中奖，其余未中奖，
则三次中奖的所有情况如下：(1,4,7)，(2,4,7)，(2,5,7)，(2,5,8)，(3,4,7)，(3,5,7)，(3,5,8)，(3,6,7)，(3,6,8)，(3,6,9)，
故仅三次中奖的概率为：
Q1×Q22×23×13×3+Q22×Q3×23×13×3+Q2×Q32×23×3+Q33=2082187，
所以从初始状态下连抽9次获得至少一枚勋章的概率为1−2082187=19792187．
【解析】(1)根据概率的乘法公式计算即可；
(2)分别求出第一次中奖，第n次抽奖中奖的概率，第一次未中奖而第二次中奖，第n次抽奖中奖的概率，前两次均未中奖，第n次抽奖中奖的概率，即可得解；
(3)由题意知每抽三次至少有一次中奖，故连抽9次至少中奖3次，故只需排除3次中奖的情况即可获得一枚优胜者勋章，另外，每两次中奖的间隔不能超过三次，每次中奖后袋中的球会回到初始状态，分别从初始状态开始，抽一次中奖的概率，从初始状态开始抽两次，第一次未中奖而第二次中奖的概率，从初始状态开始抽三次，前两次均未中奖而第三次中奖的概率，再求出仅三次中奖的概率即可得解．