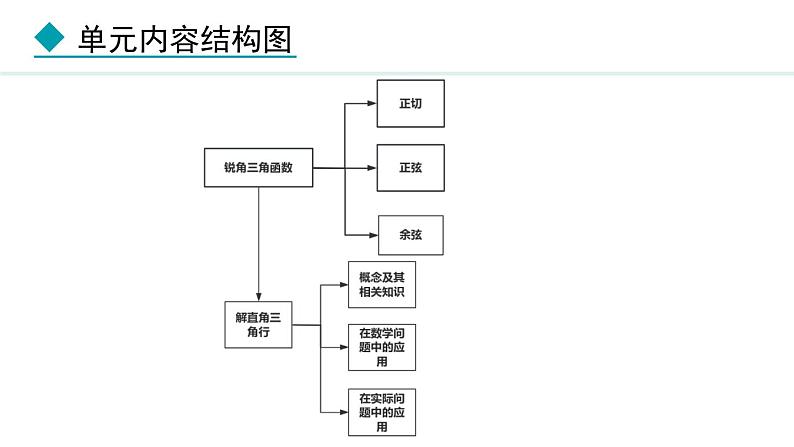
初中数学冀教版九年级上册26.1 锐角三角函数课堂教学课件ppt

这是一份初中数学冀教版九年级上册26.1 锐角三角函数课堂教学课件ppt，共23页。PPT课件主要包含了三角形相似，引导思考，正切的定义等内容，欢迎下载使用。

1.利用相似的直角三角形，探索并认识锐角三角函数tanA, 知道30°, 45°, 60°角的三角函数值．2.理解正切概念并根据正切概念正确进行计算．3.引导学生体验数学活动中充满着探索与发现，并使之能积极 参与数学学习活动，学会用数学的思维方式思考、发现、 总结、验证．
学习重点：正确认识理解正切的概念，会根据边长求出正切值学习难点：引导学生比较、分析并得出：在直角三角形中， 对任意锐角，它的对边与邻边的比值是固定的事实
思考 ：1.函数的概念及表示函数的方法；2.列举我们已经学习过的函数.
如图,轮船在A处时,灯塔B位于它的北偏东35°的方向上.轮船向东航行5 km到达C处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
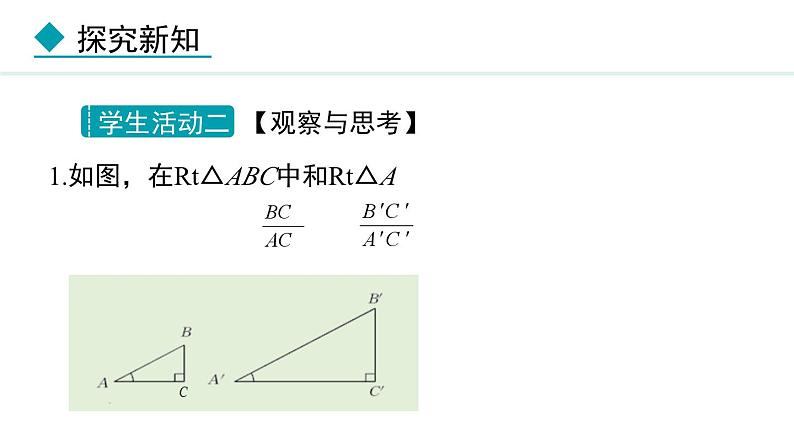
1.如图，在Rt△ABC中和Rt△A’B’C’中，∠C=∠C’=90°.当 ∠A=∠A’时， 与 具有怎样的关系?

(1)如何证明线段成比例?
(2)你能证明这两个直角三角形相似吗?
(∵∠A=∠A',∠C=∠C'=90°,∴Rt△ABC∽Rt△A'B'C')
(3)由三角形相似的性质可以得到 与 之间的关系吗?
（Rt△ABC∽Rt△A'B'C', ∴
当直角三角形中一锐角确定时，其对边与邻边的比值也随之确定。
在Rt△ABC中，∠C＝90°思考：(1)∠B的对边和邻边分别是哪两条边，tanB等于什么？(2)tanA与tan B之间有怎样的关系？
例1:在Rt△ABC中,∠C= 90°.(1)如图(1)所示,∠A=30°,求tanA,tanB 的值.(2)如图(2)所示,∠A=45°,求tanA的值.
如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD＝____．
锐角三角函数（第1课时）
1.正切函数定义：在直角三角形中，一锐角的对边与邻边的比，叫做这个角的正切。
1.把△ABC三边的长度都扩大为原来的3倍,则锐角A的 正切值(　　) A.不变 B.缩小为原来的 C.扩大为原来的3倍 D.不能确定