初中数学华师大版八年级上册3 边角边备课ppt课件

这是一份初中数学华师大版八年级上册3 边角边备课ppt课件，共18页。
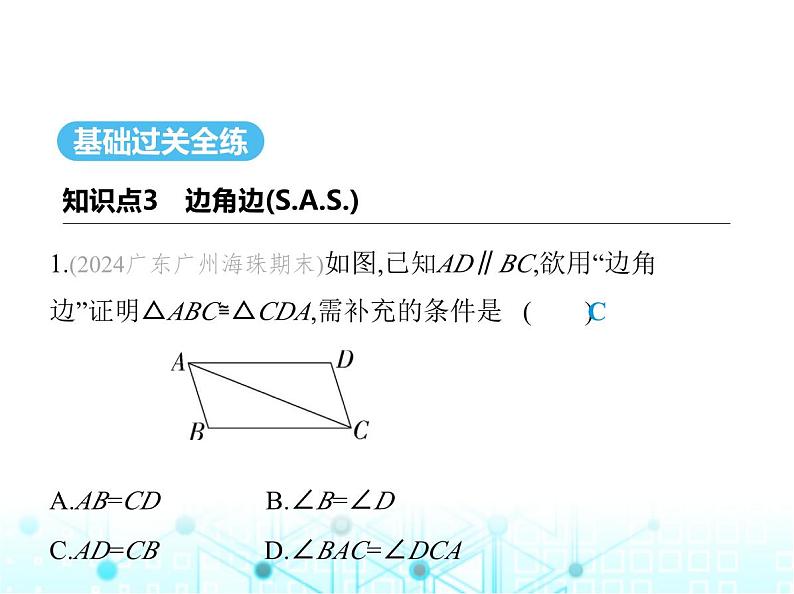
1.(2024广东广州海珠期末)如图,已知AD∥BC,欲用“边角 边”证明△ABC≌△CDA,需补充的条件是 (　    ) A.AB=CD　　　    B.∠B=∠DC.AD=CB　　　    D.∠BAC=∠DCA
解析　需补充的条件是AD=CB.理由:∵AD∥BC,∴∠DAC=∠BCA,在△ABC和△CDA中, ∴△ABC≌△CDA().故选C.
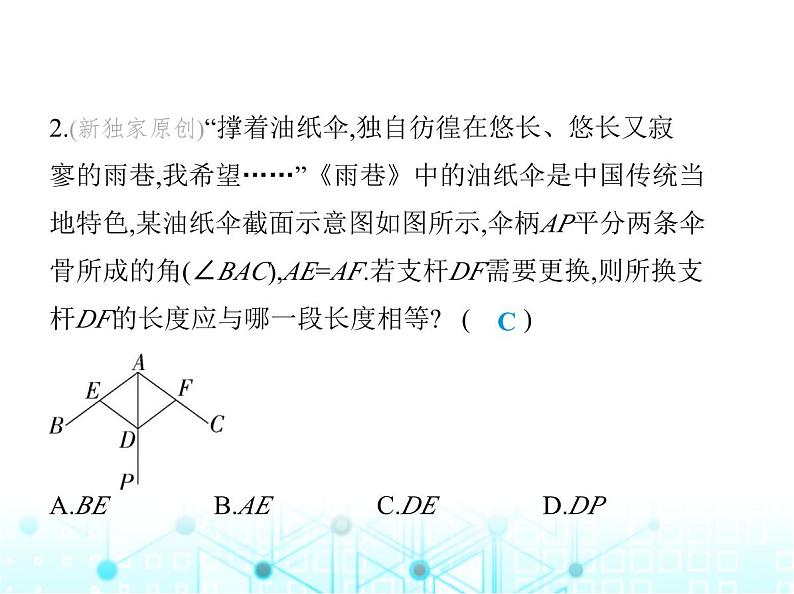
2.(新独家原创)“撑着油纸伞,独自彷徨在悠长、悠长又寂 寥的雨巷,我希望……”《雨巷》中的油纸伞是中国传统当 地特色,某油纸伞截面示意图如图所示,伞柄AP平分两条伞 骨所成的角(∠BAC),AE=AF.若支杆DF需要更换,则所换支 杆DF的长度应与哪一段长度相等? (　    ) A.BE　　　    B.AE　　　    C.DE　　　    D.DP
解析　∵AP平分∠BAC,∴∠EAD=∠FAD,在△ADE与△ ADF中, ∴△ADE≌△ADF(),∴DF=DE,即所换支杆DF的长度应与DE的长度相等.故选C.
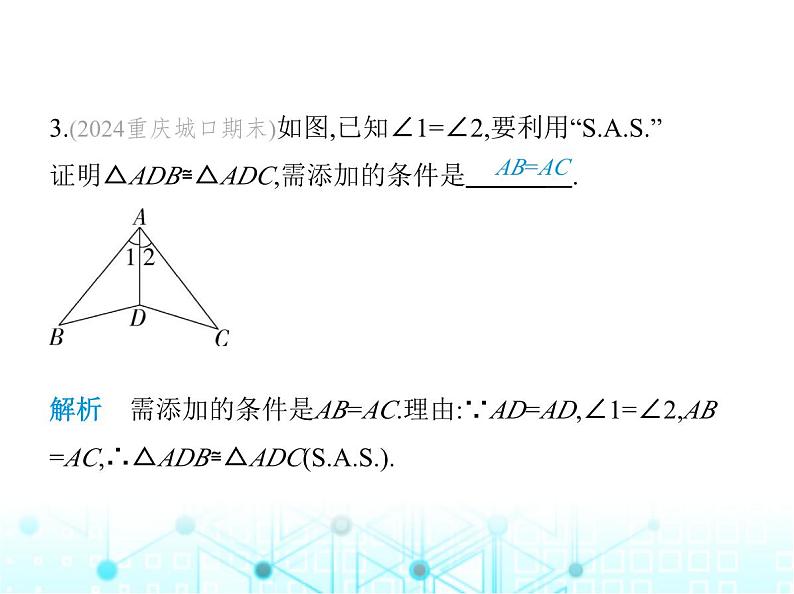
3.(2024重庆城口期末)如图,已知∠1=∠2,要利用“” 证明△ADB≌△ADC,需添加的条件是　　　    . 
解析　需添加的条件是AB=AC.理由:∵AD=AD,∠1=∠2,AB =AC,∴△ADB≌△ADC().
4.(8字模型)(教材变式·P64例1)(2023四川巴中平昌期末)如 图,在△AOD和△BOC中,AB与CD相交于点O,AO=BO,CO= DO.求证:(1)△AOD≌△BOC.(2)AD∥BC. 
证明    (1)在△AOD和△BOC中, ∴△AOD≌△BOC().(2)∵△AOD≌△BOC,∴∠A=∠B,∴AD∥BC.
5.(2024福建泉州石狮期末,9,★★☆)如图,小亮要测量池塘A, B两端的距离,他设计了一个测量方案.先在平地上取可以直 接到达A点和B点的C,D两点,AC与BD相交于点O,且AC=BD= 40 m,OA=OD,又测得△COD的周长为70 m,则A,B两端的距 离为 (　    )A.10 m　　　    B.20 m　　　    C.30 m　　　    D.35 m
解析　∵AC=BD,OA=OD,∴AC-OA=BD-OD,即OC=OB,在△COD和△BOA中, ∴△COD≌△BOA(),∴CD=AB,∵△COD的周长为70 m,∴OC+OD+CD=70 m,∴OC+OA+CD=70 m,即AC+CD=70 m,∵AC=40 m,∴CD=30 m,∴AB=30 m.故选C.
6.(平移模型)(2023四川宜宾中考,20,★☆☆)已知:如图,AB∥ DE,AB=DE,AF=DC.求证:∠B=∠E. 
证明　∵AF=DC,∴AF+CF=DC+CF,即AC=DF,∵AB∥DE,∴∠A=∠D,在△ABC和△DEF中, ∴△ABC≌△DEF(),∴∠B=∠E.
7.(2023陕西中考,18,★★☆)如图,在△ABC中,∠B=50°,∠C= 20°.过点A作AE⊥BC,垂足为E,延长EA至点D,使AD=AC.在边 AC上截取AF=AB,连结DF.求证:DF=CB. 
证明　在△ABC中,∠B=50°,∠C=20°,∴∠CAB=180°-∠B-∠C=110°.∵AE⊥BC,∴∠AEC=90°.∴∠DAF=∠AEC+∠C=110°,∴∠DAF=∠CAB.在△DAF和△CAB中, ∴△DAF≌△CAB(),∴DF=CB.
8.(2024吉林松原前郭期末,18,★★☆)已知:P是线段AB的中 点,∠1=∠2,PD=PC.求证:∠C=∠D. 
证明　∵P是线段AB的中点,∴PA=PB,∵∠1=∠2,∴∠1+∠EPF=∠2+∠EPF,即∠APD=∠BPC,在 △APD和△BPC中, ∴△APD≌△BPC(),∴∠C=∠D.
9.(推理能力)(动点问题)如图1,AB=7 cm,CA⊥AB,DB⊥AB,垂 足分别为A、B,AC=5 cm.点P在线段AB上以2 cm/s的速度由 点A向点B运动,同时点Q在射线BD上运动.它们运动的时间 为t(s)(当点P的运动结束时,点Q的运动随之结束).  图1 图2
(1)若点Q的运动速度与点P的运动速度相等,则当t=1时,△ ACP与△BPQ是否全等?并判断此时线段PC和线段PQ的位 置关系,请分别说明理由.(2)如图2,若“CA⊥AB,DB⊥AB”改为“∠CAB=∠DBA”, 点Q的运动速度为x cm/s,其他条件不变,当点P、Q运动到何处时有△ACP与△BPQ全等?求出相应的x的值.
解析    (1)△ACP≌△BPQ,PC⊥PQ.理由:∵CA⊥AB,DB⊥AB,∴∠A=∠B=90°,由题意得AP=BQ=2,∴ BP=5,∴BP=AC,在△ACP和△BPQ中, ∴△ACP≌△BPQ(),∴∠C=∠BPQ,∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,∴∠CPQ=90°,∴PC⊥PQ.