2025年高考数学一轮复习（基础版）课时精讲第5章　§5.1　平面向量的概念及线性运算（2份打包，原卷版+含解析）

这是一份2025年高考数学一轮复习（基础版）课时精讲第5章　§5.1　平面向量的概念及线性运算（2份打包，原卷版+含解析），文件包含2025年高考数学一轮复习基础版课时精讲第5章§51平面向量的概念及线性运算原卷版doc、2025年高考数学一轮复习基础版课时精讲第5章§51平面向量的概念及线性运算含解析doc等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
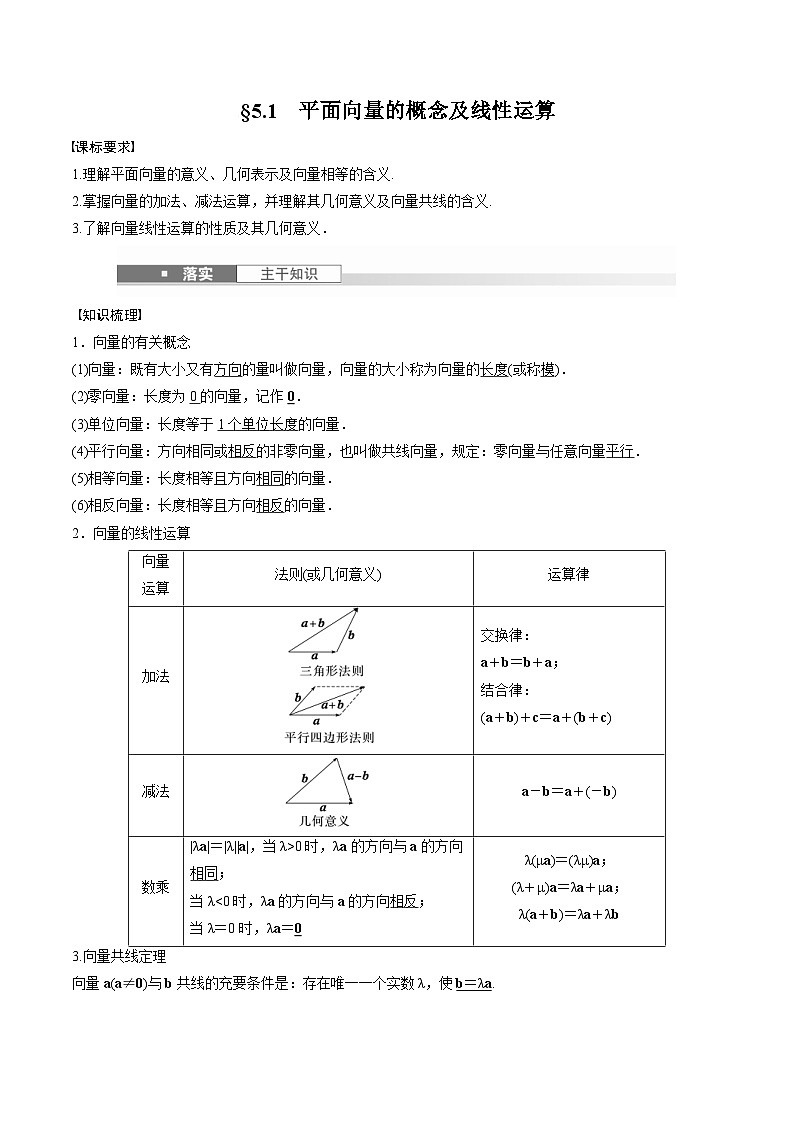
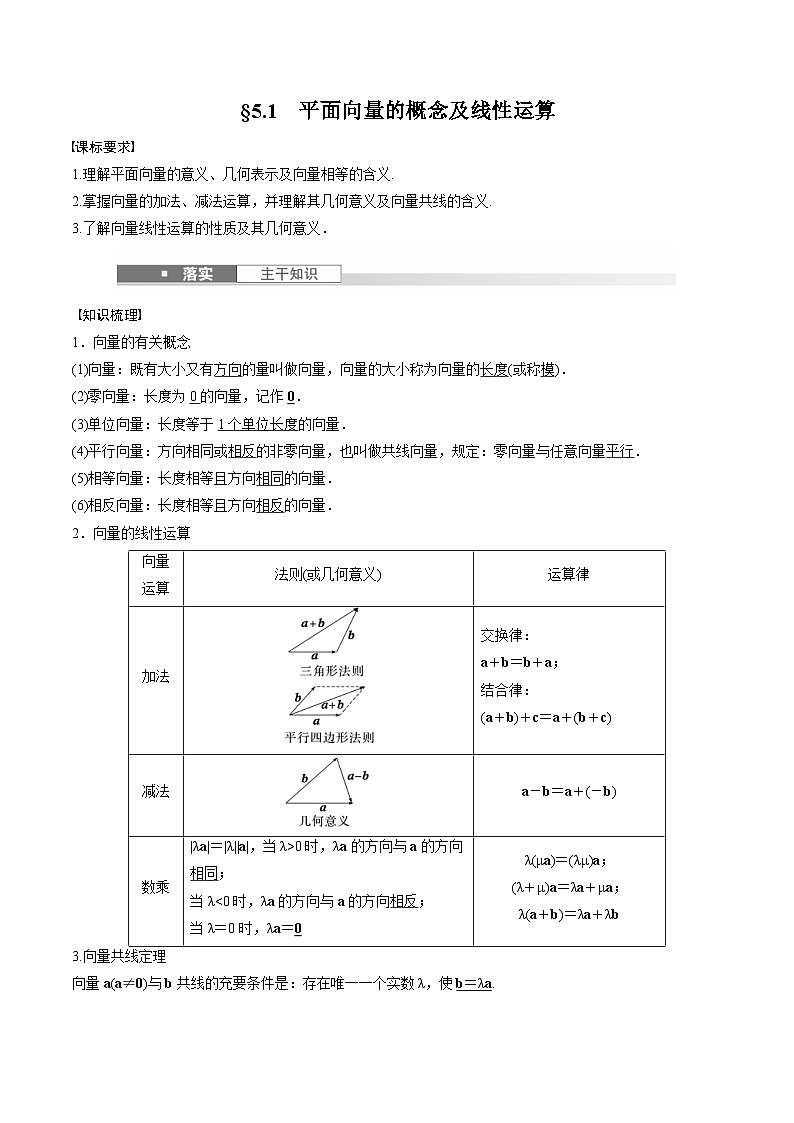
1.理解平面向量的意义、几何表示及向量相等的含义.
2.掌握向量的加法、减法运算，并理解其几何意义及向量共线的含义.
3.了解向量线性运算的性质及其几何意义．
知识梳理
1．向量的有关概念
(1)向量：既有大小又有方向的量叫做向量，向量的大小称为向量的长度(或称模)．
(2)零向量：长度为0的向量，记作0．
(3)单位向量：长度等于1个单位长度的向量．
(4)平行向量：方向相同或相反的非零向量，也叫做共线向量，规定：零向量与任意向量平行．
(5)相等向量：长度相等且方向相同的向量．
(6)相反向量：长度相等且方向相反的向量．
2．向量的线性运算
3.向量共线定理
向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ，使b＝λa.
常用结论
1．一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即eq \(A1A2,\s\up6(—→))＋eq \(A2A3,\s\up6(—→))＋eq \(A3A4,\s\up6(—→))＋…＋eq \(An－1An,\s\up6(———→))＝eq \(A1An,\s\up6(—→))，特别地，一个封闭图形，首尾连接而成的向量和为零向量．
2．在△ABC中，D为BC的中点，则eq \(AD,\s\up6(→))＝eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))．
3．在△ABC中，点P满足eq \(PA,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝0⇔P为△ABC的重心，eq \(AP,\s\up6(→))＝eq \f(1,3)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))．
4．对于任意两个向量a，b，都有||a|－|b||≤|a±b|≤|a|＋|b|.
自主诊断
1．判断下列结论是否正确．(请在括号中打“√”或“×”)
(1)若向量a与b同向，且|a|>|b|，则a>b.( )
(2)单位向量都相等．( )
(3)任一非零向量都可以平行移动．( )
(4)起点不同，但方向相同且模相等的向量是相等向量．( )
2．下列命题正确的是( )
A．零向量是唯一没有方向的向量
B．若|a|＝|b|，则a＝b或a＝－b
C．向量eq \(AB,\s\up6(→))与eq \(BA,\s\up6(→))是平行向量
D．平行向量不一定是共线向量
3．(多选)下列各式化简结果正确的是( )
A.eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→))＝eq \(BC,\s\up6(→)) B.eq \(AM,\s\up6(→))＋eq \(MB,\s\up6(→))＋eq \(BO,\s\up6(→))＋eq \(OM,\s\up6(→))＝eq \(AM,\s\up6(→))
C.eq \(AB,\s\up6(→))＋eq \(BC,\s\up6(→))－eq \(AC,\s\up6(→))＝0 D.eq \(AB,\s\up6(→))－eq \(AD,\s\up6(→))－eq \(DC,\s\up6(→))＝eq \(BC,\s\up6(→))
4．已知e1，e2为平面内两个不共线的向量，eq \(MN,\s\up6(→))＝2e1－3e2，eq \(NP,\s\up6(→))＝λe1＋6e2，若M，N，P三点共线，则λ＝________.
题型一 平面向量的基本概念
例1 (1)(多选)下列说法正确的是( )
A．若a＝b，b＝c，则a＝c
B．若四边形ABCD满足eq \(AB,\s\up6(→))＝eq \(DC,\s\up6(→))，则四边形ABCD是平行四边形
C．若a∥b，b∥c，则a∥c
D．与非零向量a共线的单位向量为±eq \f(a,|a|)
(2)如图，在等腰梯形ABCD中，对角线AC与BD交于点P，点E，F分别在两腰AD，BC上，EF过点P，且EF∥AB，则下列等式中成立的是( )
A.eq \(AD,\s\up6(→))＝eq \(BC,\s\up6(→)) B.eq \(AC,\s\up6(→))＝eq \(BD,\s\up6(→)) C.eq \(PE,\s\up6(→))＝eq \(PF,\s\up6(→)) D.eq \(EP,\s\up6(→))＝eq \(PF,\s\up6(→))
跟踪训练1 (1)(多选)下列关于向量的说法正确的是( )
A．若|a|＝0，则a＝0
B．若向量eq \(AB,\s\up6(→))与eq \(CD,\s\up6(→))是共线向量，则A，B，C，D四点必在同一条直线上
C．对于任意向量a，b，必有|a＋b|≤|a|＋|b|
D．若a∥b，则存在唯一实数λ，使a＝λb
(2)(多选)如图所示，四边形ABCD，CEFG，CGHD是全等的菱形，则下列结论中一定成立的是( )
A．|eq \(AB,\s\up6(→))|＝|eq \(EF,\s\up6(→))| B.eq \(AB,\s\up6(→))与eq \(FH,\s\up6(→))共线 C.eq \(BD,\s\up6(→))与eq \(EH,\s\up6(→))共线 D.eq \(CD,\s\up6(→))＝eq \(FG,\s\up6(→))
题型二 平面向量的线性运算
命题点1 向量加、减法的几何意义
例2 若|eq \(AB,\s\up6(→))|＝7，|eq \(AC,\s\up6(→))|＝4，则|eq \(BC,\s\up6(→))| 的取值范围是( )
A．[3,7] B．(3,7) C．[3,11] D．(3,11)
命题点2 向量的线性运算
例3 在△ABC中，点D在边AB上，BD＝2DA.记eq \(CA,\s\up6(→))＝m，eq \(CD,\s\up6(→))＝n，则eq \(CB,\s\up6(→))等于( )
A．3m－2n B．－2m＋3n C．3m＋2n D．2m＋3n
命题点3 根据向量线性运算求参数
例4 已知矩形ABCD的对角线交于点O，E为AO的中点，若eq \(DE,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(AD,\s\up6(→))(λ，μ为实数)，则λ2－μ2等于( )
A．－eq \f(1,2) B.eq \f(7,9) C.eq \f(3－2\r(2),2) D.eq \f(1＋\r(2),2)
跟踪训练2
(1)如图所示，在平行四边形ABCD中，AC与BD交于点O，E是OD的中点，AE的延长线交CD于点F.若eq \(AB,\s\up6(→))＝a，eq \(AD,\s\up6(→))＝b，则eq \(AF,\s\up6(→))等于( )
A.eq \f(1,4)a＋b B.eq \f(1,3)a＋b C.eq \f(1,4)a＋eq \f(1,3)b D.eq \f(1,3)a＋eq \f(1,3)b
(2)M是△ABC内的一点，若eq \(BM,\s\up6(→))＝eq \f(1,3)eq \(BA,\s\up6(→))＋λeq \(BC,\s\up6(→))，eq \(AM,\s\up6(→))＝eq \f(1,2)eq \(AB,\s\up6(→))＋μeq \(AC,\s\up6(→))，则λ＋μ等于( )
A.eq \f(7,6) B．1 C.eq \f(5,6) D.eq \f(1,3)
题型三 共线定理及其应用
例5 已知向量a，b不共线，向量8a－kb与－ka＋b共线，则k＝________.
跟踪训练3 (1)已知平面向量a，b不共线，eq \(AB,\s\up6(→))＝4a＋6b，eq \(BC,\s\up6(→))＝－a＋3b，eq \(CD,\s\up6(→))＝a＋3b，则( )
A．A，B，D三点共线 B．A，B，C三点共线
C．B，C，D三点共线 D．A，C，D三点共线
(2)如图，在△ABC中，eq \(AN,\s\up6(→))＝eq \f(1,2)eq \(NC,\s\up6(→))，P是BN的中点，若eq \(AP,\s\up6(→))＝meq \(AB,\s\up6(→))＋eq \f(1,4)eq \(AC,\s\up6(→))，则实数m的值是________．
课时精练
一、单项选择题
1．如图，在正六边形ABCDEF中，eq \(AF,\s\up6(→))－eq \(ED,\s\up6(→))＋eq \(EF,\s\up6(→))＋2eq \(AB,\s\up6(→))等于( )
A．0 B.eq \(AB,\s\up6(→)) C.eq \(AD,\s\up6(→)) D.eq \(CF,\s\up6(→))
2.如图，e1，e2为互相垂直的单位向量，向量a＋b＋c可表示为( )
A．2e1－3e2 B．3e1－2e2 C．2e1＋3e2 D．3e1＋2e2
3．若a，b为非零向量，则“eq \f(a,|a|)＝eq \f(b,|b|)”是“a，b共线”的( )
A．充要条件 B．充分不必要条件
C．必要不充分条件 D．既不充分也不必要条件
4．已知向量a，b不共线，且c＝xa＋b，d＝a＋(2x－1)b，若c与d方向相反，则实数x的值为( )
A．1 B．－eq \f(1,2) C．1或－eq \f(1,2) D．－1或－eq \f(1,2)
二、多项选择题
5．下列各式中能化简为eq \(AD,\s\up6(→))的是( )
A．－(eq \(CB,\s\up6(→))＋eq \(MC,\s\up6(→)))－(eq \(DA,\s\up6(→))＋eq \(BM,\s\up6(→))) B．－eq \(BM,\s\up6(→))－eq \(DA,\s\up6(→))＋eq \(MB,\s\up6(→))
C．(eq \(AB,\s\up6(→))－eq \(DC,\s\up6(→)))－eq \(CB,\s\up6(→)) D.eq \(AD,\s\up6(→))－(eq \(CD,\s\up6(→))＋eq \(DC,\s\up6(→)))
6.如图，在四边形ABCD中，AB∥CD，AB⊥AD，AB＝2AD＝2DC，E为BC边上一点，且eq \(BC,\s\up6(→))＝3eq \(EC,\s\up6(→))，F为AE的中点，则( )
A.eq \(BC,\s\up6(→))＝－eq \f(1,2)eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→)) B.eq \(AF,\s\up6(→))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(1,3)eq \(AD,\s\up6(→))
C.eq \(BF,\s\up6(→))＝－eq \f(2,3)eq \(AB,\s\up6(→))＋eq \f(1,3)eq \(AD,\s\up6(→)) D.eq \(CF,\s\up6(→))＝eq \f(1,6)eq \(AB,\s\up6(→))－eq \f(2,3)eq \(AD,\s\up6(→))
三、填空题
7．已知在四边形ABCD中，eq \(AB,\s\up6(→))＝eq \f(1,2)eq \(DC,\s\up6(→))，且|eq \(AD,\s\up6(→))|＝|eq \(BC,\s\up6(→))|，则四边形ABCD的形状是________．
8.如图，已知菱形ABCD的边长为2，∠BAD＝120°，点E，F分别在边BC，CD上，且满足eq \(BE,\s\up6(→))＝eq \(EC,\s\up6(→))，eq \(CD,\s\up6(→))＝2eq \(CF,\s\up6(→))，则|eq \(AE,\s\up6(→))＋eq \(AF,\s\up6(→))|＝________.
四、解答题
9．如图，在矩形ABCD中，eq \(DE,\s\up6(→))＝2eq \(EC,\s\up6(→))，eq \(BF,\s\up6(→))＝2eq \(FC,\s\up6(→))，AC与EF交于点N.
(1)若eq \(CN,\s\up6(→))＝λeq \(AB,\s\up6(→))＋μeq \(AD,\s\up6(→))，求λ＋μ的值；
(2)设eq \(AE,\s\up6(→))＝a，eq \(AF,\s\up6(→))＝b，试用a，b表示eq \(AC,\s\up6(→)).
10.如图所示，在△ABC中，D，F分别是BC，AC的中点，eq \(AE,\s\up6(→))＝eq \f(2,3)eq \(AD,\s\up6(→))，eq \(AB,\s\up6(→))＝a，eq \(AC,\s\up6(→))＝b.
(1)用a，b表示eq \(AE,\s\up6(→))，eq \(BE,\s\up6(→))；
(2)求证：B，E，F三点共线．
11.如图，已知A，B，C是圆O上不同的三点，CO与AB交于点D(点O与点D不重合)，若eq \(OC,\s\up6(→))＝λeq \(OA,\s\up6(→))＋μeq \(OB,\s\up6(→))(λ，μ∈R)，则λ＋μ的取值范围是________．
向量
运算
法则(或几何意义)
运算律
加法
交换律：
a＋b＝b＋a；
结合律：
(a＋b)＋c＝a＋(b＋c)
减法
a－b＝a＋(－b)
数乘
|λa|＝|λ||a|，当λ>0时，λa的方向与a的方向相同；
当λ