

2023-2024学年吉林省长春市榆树市七年级(下)期末数学试卷(含答案)
展开1.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A. 斐波那契螺旋线B. 笛卡尔心形线
C. 赵爽弦图D. 科克曲线
2.下列各式中,是一元一次方程的是( )
A. 2x−1<3B. x−1=0C. 5−4=1D. x+3
3.下列解方程变形正确的是( )
A. 由3+x=5,得x=5+3B. 由12x=0,得x=2
C. 由7x=−4,得x=−47D. 由3=x−2,得x=−2−3
4.若一个多边形每一个内角都为144°,则这个多边形是( )边形.
A. 6B. 8C. 10D. 12
5.已知a>b,下列式子不一定成立的是( )
A. a−1>b−1B. −2a<−2bC. 12a+1>12b+1D. ma
A. 正五边形B. 正六边形C. 正八边形D. 正十边形
7.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A. 中线
B. 中位线
C. 高线
D. 角平分线
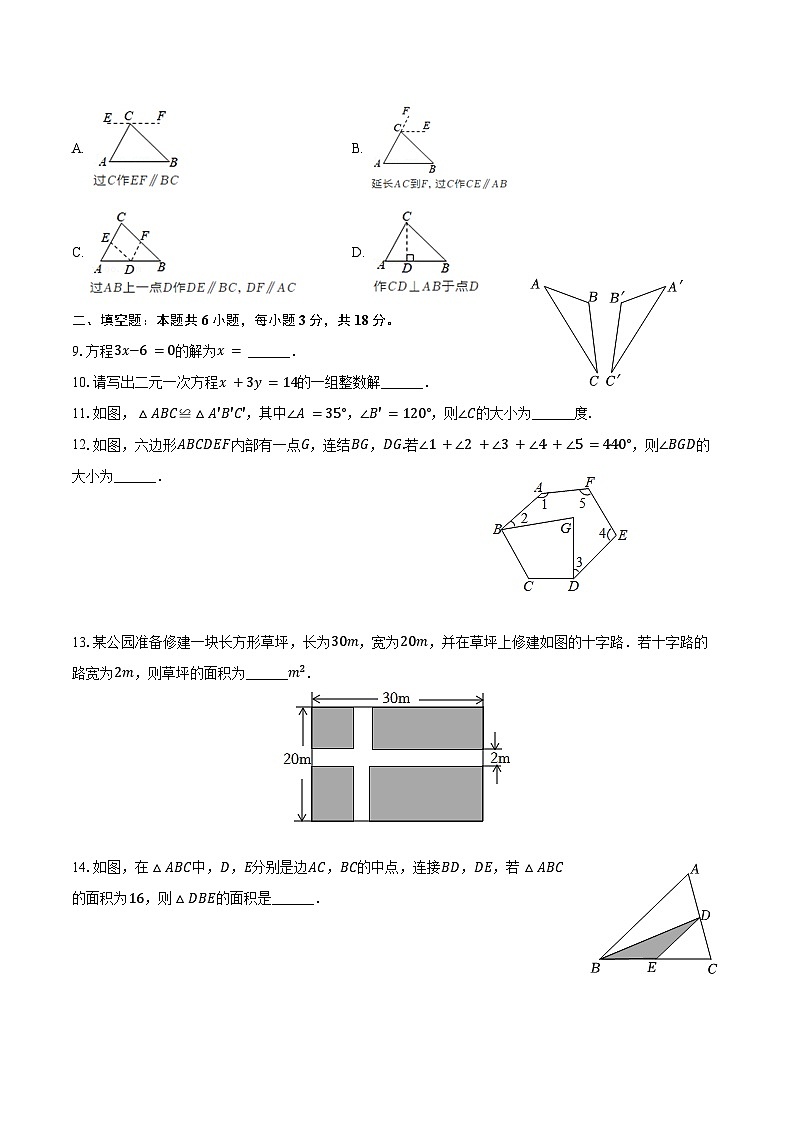
8.在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如图所示四种辅助线,其中不能证明“三角形内角和是180°”的是( )
A. B.
C. D.
二、填空题:本题共6小题,每小题3分,共18分。
9.方程3x−6=0的解为x= ______.
10.请写出二元一次方程x+3y=14的一组整数解______.
11.如图,△ABC≌△A′B′C′,其中∠A=35°,∠B′=120°,则∠C的大小为______度.
12.如图,六边形ABCDEF内部有一点G,连结BG,DG.若∠1+∠2+∠3+∠4+∠5=440°,则∠BGD的大小为______.
13.某公园准备修建一块长方形草坪,长为30m,宽为20m,并在草坪上修建如图的十字路.若十字路的路宽为2m,则草坪的面积为______m2.
14.如图,在△ABC中,D,E分别是边AC,BC的中点,连接BD,DE,若△ABC的面积为16,则△DBE的面积是______.
三、计算题:本大题共1小题,共5分。
15.解方程3x−12=4x+25−1
四、解答题:本题共7小题,共57分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题6分)
解方程组:3x+y=6,x−2y=9..
17.(本小题7分)
解不等式组:3x−(x−2)≤6x−1<4x+13并将解集在数轴上表示.
18.(本小题7分)
对于下列问题,在解答过程的空白处填上适当的内容(理由或数学式).
如图,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°.
(1)求∠EBC的度数;
(2)求∠A的度数.
解:(1)∵CD⊥AB(已知),
∴∠CDB=______°.
∵∠EBC=∠CDB+∠BCD(______).
∴∠EBC=______°+35°=______°(等量代换).
(2)∵∠EBC=∠A+∠ACB(______),
∴∠A=∠EBC−∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=______−90°=______°(等量代换).
19.(本小题8分)
树市某中学七年一班全体学生参加团活动进行分组,原来每组8人,后来重新编组,每组12人,这样就比原来减少2组,请问七年一班共有多少人?
20.(本小题8分)
如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多1,AB与AC的和为11.
(1)求AB、AC的长;
(2)求BC边的取值范围.
21.(本小题9分)
如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.
22.(本小题12分)
已知数轴上的原点为O,A、B、C三点对应的数分别为−16,8和12,动点P从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,动点Q从点C出发,以每秒1个单位的速度沿数轴负方向运动,设点P的运动时间为t秒.
(1)线段AB的长为______,线段AC的长为______.
(2)当点P运动到与点A、B距离相等时,求点P表示的数.
(3)当P、Q两点相遇时,求t的值.
(4)当PO+QB=10时,直接写出t的值.
参考答案
1.D
2.B
3.C
4.C
5.D
6.C
7.D
8.D
9.2
10.x=14y=0(答案不唯一).
11.25
12.80°
13.504
14.4
15.解:去分母得:5(3x−1)=2(4x+2)−10,
去括号得:15x−5=8x+4−10,
移项得:15x−8x=4−10+5,
合并同类项得:7x=−1,
系数化为得:x=−17.
16.解:方程组3x+y=6①x−2y=9②,
①×2+②得:7x=21,
解得:x=3,
把x=3代入①得:9+y=6,
解得:y=−3,
则方程组的解为x=3y=−3.
17.解:3x−(x−2)≤6①x−1<4x+13②,
由①得x≤2.
由②得x>−4.
所以原不等式组的解集为−4
18.(1)∵CD⊥AB(已知),
∴∠CDB=90°.
∵∠EBC=∠CDB+∠BCD(三角形的一个外角等于与它不相邻的两个内角和).
∴∠EBC=90°+35°=125°(等量代换).
(2)∵∠EBC=∠A+∠ACB(三角形的一个外角等于与它不相邻的两个内角和),
∴∠A=∠EBC−∠ACB(等式的性质).
∵∠ACB=90°(已知),
∴∠A=125°−90°=35°(等量代换).
19.解:设七年一班共有x人,
依题意得:x8−x12=2,
解得:x=48.
答:七年一班共有48人.
20.解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长−△ADC的周长=(AB+AD+BD)−(AC+AD+CD)=AB−AC=1,
即AB−AC=2①,
又AB+AC=11②,
①+②得.2AB=12,
解得AB=6,
②−①得,2AC=10,
解得AC=5,
∴AB和AC的长分别为:AB=6,AC=5;
(2)∵AB=6,AC=5,
∴1
(2)5;
(3)∵由平移变换的性质得:BC//EF,AE//CF,
∴∠E=∠ABC=75°,
∴∠CFE+∠E=180°,
∴∠CFE=105°.
22.(1)线段AB的长为24,线段AC的长为28;
(2)设点p表示的数为x,则
x−(−16)=8−x,
解得x=−4,即点p表示的数为−4;
(3)由题意得:
2t+t=28,
解得t=283;
(4)t=103或t=10.
2022-2023学年吉林省长春市榆树市七年级(上)期末数学试卷(含答案解析): 这是一份2022-2023学年吉林省长春市榆树市七年级(上)期末数学试卷(含答案解析),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含答案解析): 这是一份2022-2023学年吉林省长春市榆树市八号镇七年级(下)期末数学试卷(含答案解析),共14页。试卷主要包含了 若x2=4,则x的值, 下列数中227,0,101001C, 计算 2=______ 等内容,欢迎下载使用。
2022-2023学年吉林省长春市榆树市慧望中学七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年吉林省长春市榆树市慧望中学七年级(下)期末数学试卷(含解析),共13页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












