青岛版初中八年级数学上册专项素养综合练(二)构造全等三角形的四种方法课件

这是一份青岛版初中八年级数学上册专项素养综合练(二)构造全等三角形的四种方法课件，共17页。

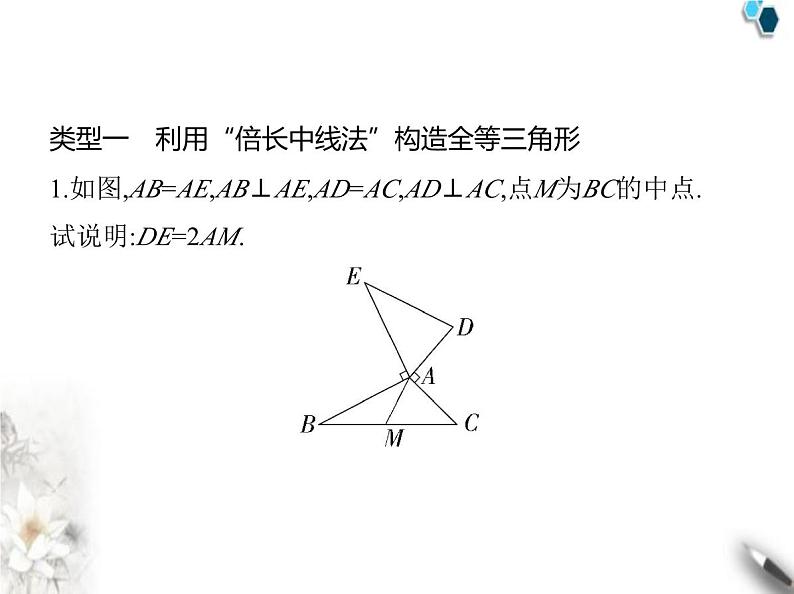
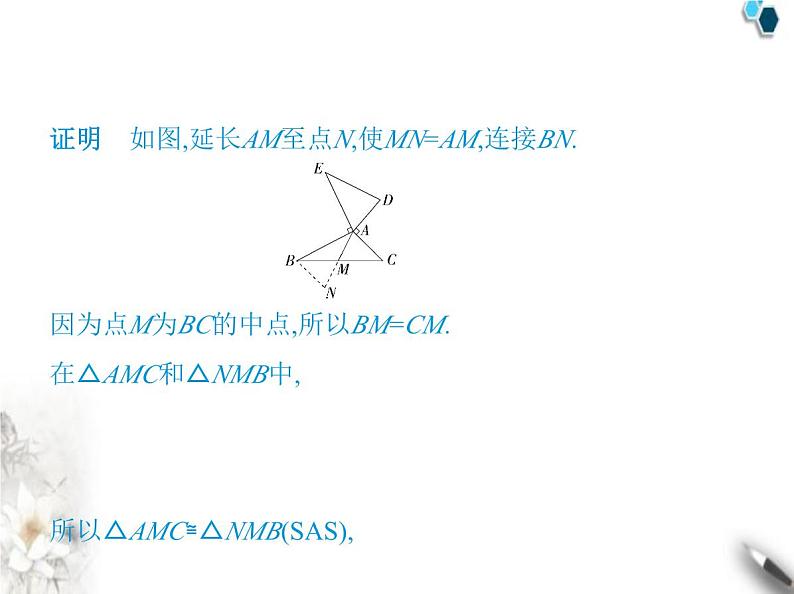
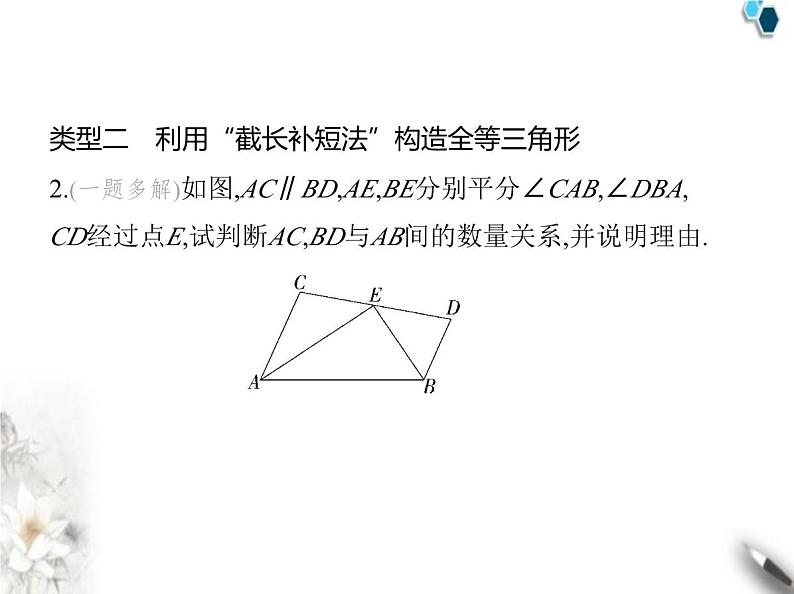
专项素养综合全练(二)构造全等三角形的四种方法类型一　利用“倍长中线法”构造全等三角形1.如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点.试说明:DE=2AM. 证明　如图,延长AM至点N,使MN=AM,连接BN.因为点M为BC的中点,所以BM=CM.在△AMC和△NMB中, 所以△AMC≌△NMB(SAS),所以AC=NB,∠C=∠NBM,所以∠ABN=∠ABC+∠NBM=∠ABC+∠C=180°-∠BAC=∠EAD.因为AD=AC,所以AD=BN.在△ABN和△EAD中, 所以△ABN≌△EAD(SAS),所以DE=NA,所以DE=2AM.类型二　利用“截长补短法”构造全等三角形2.(一题多解)如图,AC∥BD,AE,BE分别平分∠CAB,∠DBA,CD经过点E,试判断AC,BD与AB间的数量关系,并说明理由.  解析    AC+BD=AB,理由如下:方法一(截长法):如图1所示,在线段AB上截取AF=AC,连接EF. 图1因为AE,BE分别平分∠CAB,∠DBA,所以∠1=∠2,∠3=∠4.在△ACE和△AFE中, 所以△ACE≌△AFE(SAS),所以∠C=∠5.因为AC∥BD,所以∠C+∠D=180°,因为∠5+∠6=180°,所以∠D=∠6.在△EFB和△EDB中, 所以△EFB≌△EDB(AAS),所以BF=BD,所以AB=AF+BF=AC+BD,即AC+BD=AB.方法二(补短法):如图2所示,延长AC至点F,使AF=AB,连接EF. 图2因为AE,BE分别平分∠CAB,∠DBA,所以∠1=∠2,∠3=∠4,在△AEF和△AEB中, 所以△AEF≌△AEB(SAS),所以EF=EB,∠F=∠3.又因为∠3=∠4,所以∠F=∠4.因为AC∥BD,所以∠FCE=∠D.在△CEF和△DEB中, 所以△CEF≌△DEB(AAS),所以CF=BD.因为AB=AF=AC+CF=AC+BD,所以AC+BD=AB.类型三　利用“补形法”构造全等三角形3.如图,在△ABC中,∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE,试说明BE= AD. 类型四　利用“三垂直”构造全等三角形4.在△ABC中,∠BAC=90°,AB=AC,将△ABC放在平面直角坐标系中,如图所示. 图1 图2 图3(1)如图1,若A(1,0),B(0,3),则点C的坐标为　　　    ;(2)如图2,若A(1,3),B(-1,0),则点C的坐标为　　　    ;(3)如图3,若B(-4,0),C(0,-1),则点A的坐标为　　　    .(4,1)(4,1)解析　(1)过点C作CD⊥x轴于点D(图略),则∠CAD+∠ACD=90°.∠CDA=∠AOB=90°,因为∠BAC=90°,所以∠BAO+∠CAD=90°,所以∠BAO=∠ACD.在△ABO与△CAD中, 所以△ABO≌△CAD(AAS),所以BO=AD,OA=CD.因为A(1,0),B(0,3),所以OA=1,OB=3,所以AD=3,CD=1,所以OD=OA+AD=4,所以C(4,1).(2)过点A作AD⊥x轴于点D,过点C作CE⊥AD于点E(图略).同(1)可证△ACE≌△BAD,所以AE=BD,CE=AD.因为A(1,3),B(-1,0),所以BD=2,AD=3,所以CE=3,AE=2,所以DE=AD-AE=1,所以C(4,1).(3)过点A作AD⊥x轴于点D,AE⊥y轴于点E(图略).易得AD=OE,∠EAD=90°.同(1)可证△BAD≌△CAE,所以CE=BD,AE=AD.因为B(-4,0),C(0,-1),所以OB=4,OC=1,所以AE=OB-BD=OB-CE=OB-(OC+OE)=3-OE=3-AD=3-AE,所以AE= ,所以OE= ,所以A .