广东省茂名市电白区2023-2024学年八年级上学期期末质量监测数学试卷(含答案)

这是一份广东省茂名市电白区2023-2024学年八年级上学期期末质量监测数学试卷(含答案)，共10页。试卷主要包含了在给出的一组数-2，，，3，下列命题中，是真命题的为，点，是一次函数图象上的两点等内容，欢迎下载使用。

八年级数学
（满分：120分考试时间：120分钟）
一.选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.在给出的一组数-2，，，3.14，，中，无理数有（）
A.4个B.3个C.2个D.1个
2.下列命题中，是真命题的为（）
A.三角形的一个外角大于任何一个内角B.如果两个角相等，那么它们是对顶角
C.直角三角形的两锐角互余D.如果两个直角三角形的面积相等，那么它们全等
3.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）
A.甲B.乙C.丙D.丁
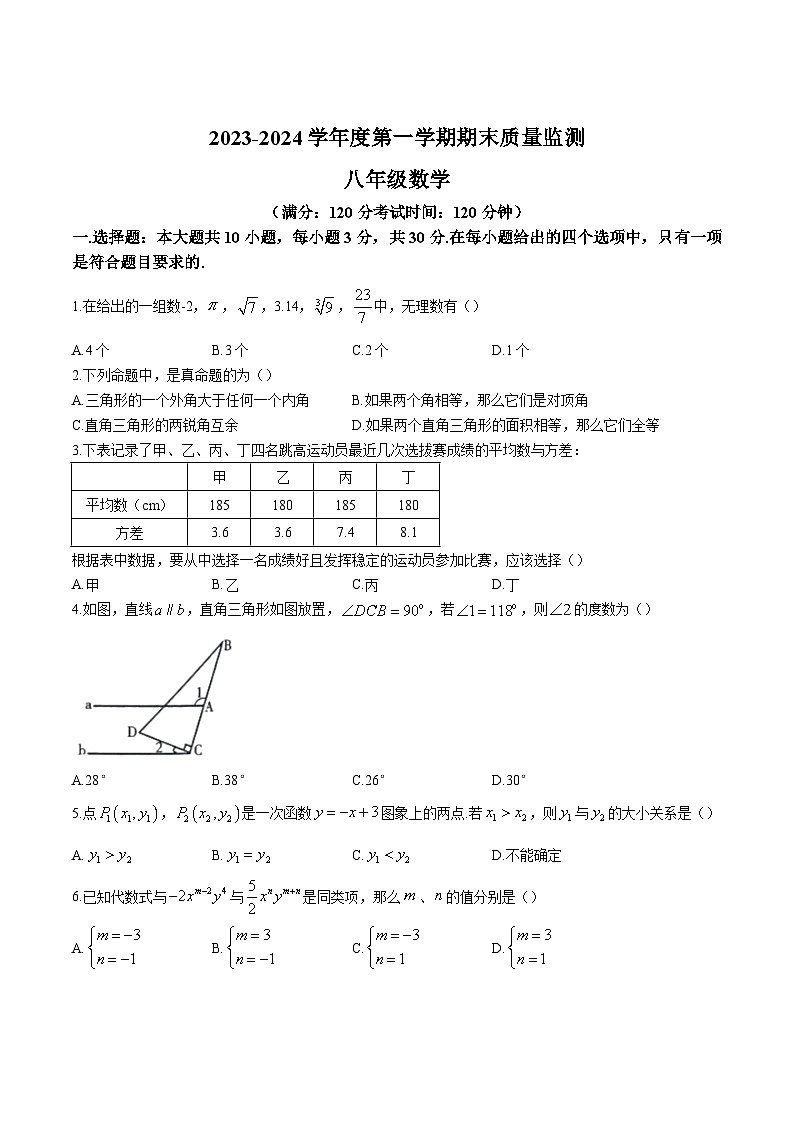
4.如图，直线，直角三角形如图放置，，若，则的度数为（）
A.28°B.38°C.26°D.30°
5.点，是一次函数图象上的两点.若，则与的大小关系是（）
A.B.C.D.不能确定
6.已知代数式与与是同类项，那么、的值分别是（）
A.B.C.D.
7.已知是二元一次方程组的解，则的平方根为（）
A.2B.C.D.
8.在同一平面直角坐标系中，函数与的图象大致是（）
A.B.C.D.
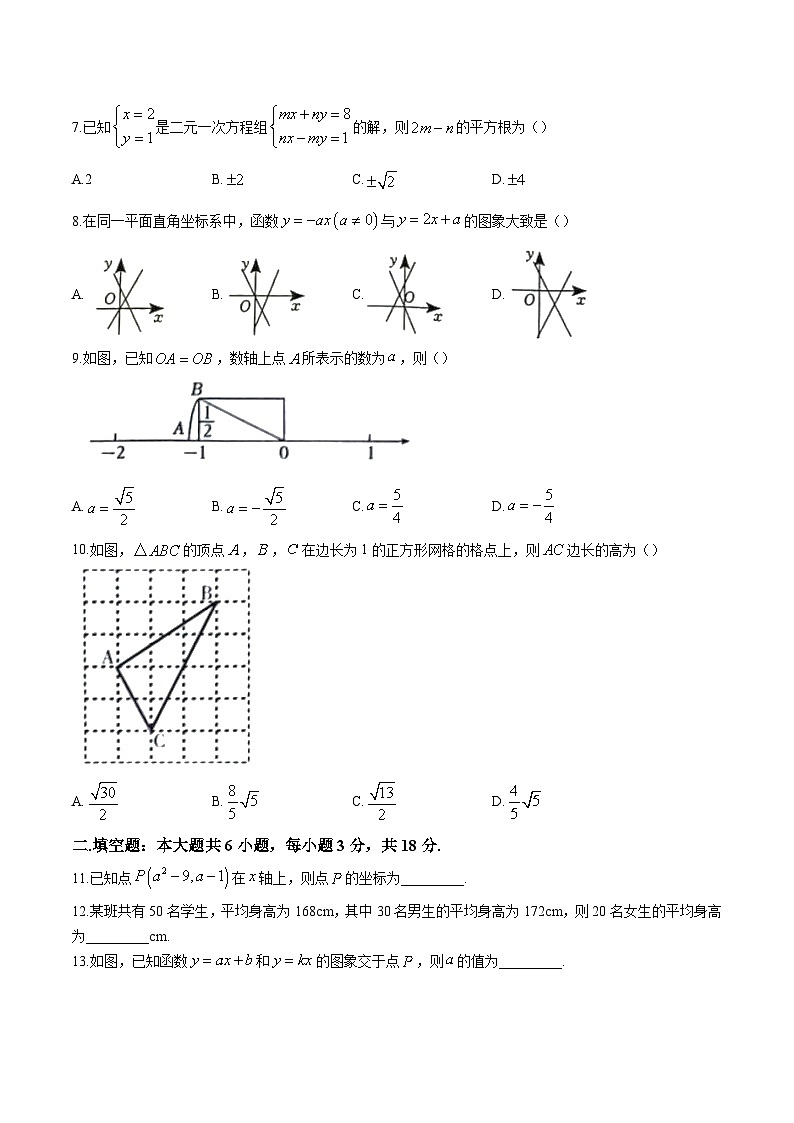
9.如图，已知，数轴上点所表示的数为，则（）
A.B.C.D.
10.如图，的顶点，，在边长为1的正方形网格的格点上，则边长的高为（）
A.B.C.D.
二.填空题：本大题共6小题，每小题3分，共18分.
11.已知点在轴上，则点的坐标为_________.
12.某班共有50名学生，平均身高为168cm，其中30名男生的平均身高为172cm，则20名女生的平均身高为_________cm.
13.如图，已知函数和的图象交于点，则的值为_________.
14.如图，在中，平分，平分，，则的度数为_________.
15.点在函数的图象上，则代数式的值等于_________.
16.我们给出定义：若三角形中一个内角是另一个内角的三分之一，我们称这个三角形是“分角三角形”，其中称为“分角”.已知一个“分角三角形”中有一个内角为60°，那么这个“分角三角形”中分角的度数是_________.
三.解答题（一）：本大题共3小题，第17题12分，第18题6分，第19题7分，共25分.
17.计算或解方程组：
（1）计算：（2）解方程组：
18.如图，，，.求证：.
19.阳光中学积极开展课后延时服务活动，提供了“有趣的生物实验，虚拟机器人竞赛，国际象棋大赛，趣味篮球训练，经典影视欣赏……”等课程供学生自由选择一个学期后，该校为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“.非常满意；.比较满意；.基本满意；.不满意”四个等级绘制成了如图所示的两幅不完整的统计图.
图①图②
请根据图中信息，解答下列问题：
（1）该校抽样调查的学生人数为_____________人，请补全条形统计图；
（2）样本中，学生对课后延时服务满意情况的“中位数”所在等级为________，“众数”所在等级为___________；（填“，，或”）
（3）若该校共有学生3000人，估计全校学生对课后延时服务满意的（包含，，三个等级）有多少人？
四.解答题（二）：本大题共3小题，每小题9分，共27分.
20.某药店出售、两种N95的口罩，已知该店进货4个种N95口罩和3个种N95口罩共需27元，进货2个种N95口罩所需费用比进货1个种N95口罩所需费用多1元.
（1）请分别求出、两种N95口罩的进价是多少元？
（2）已知药店将种N95口罩每个提价1元出售，种N95口罩每个提价20％出售，小雅在该药店购买、两种N95口罩（两种口罩均要购买）共花费36元，小雅有哪几种购买方案？
21.如图，是一张放在平面直角坐标系中的长方形纸片，为原点，点在轴的正半轴上，点在轴的正半轴上，，，在边上取一点，将纸片沿翻折，使点落在边上的点处.
（1）求、两点的坐标；
（2）求过、两点的直线函数表达式.
22.如图，直线和直线相交于点，分别与轴交于，两点.
（1）求点的坐标；
（2）在轴上有一动点，过点作轴的垂线，分别交函数和的图象于点，，若，求的值.
五.解答题（三）：本大题共2小题，每小题10分，共20分.
23.请根据函数相关知识，对函数的图象与性质进行探究，并解决相关问题.
①列表；②描点；③连线.
（1）表格中：__________，________.
（2）在直角坐标系中画出该函数图象.
（3）观察图象：
①当_________时，随的增大而增大；
②若关于的方程没有实数根，则的取值范围是___________.
24.阅读理解：已知实数，满足…①，…②，求和的值.仔细观察两个方程未知数的系数之间的关系，本题可以通过适当变形整体求得代数式的值，如由①-②可得，由①＋②×2可得.这样的解题思想就是通常所说的“整体思想”.利用“整体思想”，解决下列问题：
（1）已知二元一次方程组，则__________，_________；
（2）买10支铅笔、2块橡皮、1本日记本共需27元，买38支铅笔、5块橡皮、2本日记本共需91元，求购买2支铅笔、3块橡皮、2本日记本共需多少元？
（3）对于实数，，定义新运算：，其中，，是常数，等式右边是实数运算.已知，，求的值.
2023-2024学年度第一学期期末质量监测
八年级数学参考答案
一.选择题：
1-5：BCAAC6-10：DBCBB
二.填空题
11.12.16213.
14.70°15.202116.20°或30°
（提示：①；②，解得）
三.解答题（共8小题，满分72分）
17.解：（1）原式；
（2）解：
①-②得
将代入②中
得
原方程组的解为
18.证明：，，，
，，又，，
，.
19.解：（1）校抽样调查的学生人数为（人），
则等级的人数为（人），补充统计图如图所示，
图②
（2）解：根据题意，中位数为第25，26个数的平均数，在等级，等级人数最多，则众数在等级，故答案为：，；
（3）（人）
答：估计全校学生对课后延时服务满意的（包含，，三个等级）有2700人.
20.解：（1）设种N95口罩的进价是元，种N95口罩的进价是元，
依题意得：，解得：.
答：种N95口罩的进价是3元，种N95口罩的进价是5元.
（2）设购买种N95口罩个，种N95口罩个，
依题意得：，即
解得：.
又，均为正整数，或
小雅共有2种购买方案，
方案1：购买种N95口罩6个，种N95口罩2个；
方案2：购买种N95口罩3个，种N95口罩4个.
21.解：（1）依题意可知，折痕是四边形的对称轴，
在中，，，
由勾股定理，得，
，.
在中，由勾股定理，得，
又，，
，
解得，.所以，；
（2）设、两点所在的直线的解析式为，
则，解得，
所以过、两点的直线函数表达式为.
22.解：（1）令，解得，
，
；
（2）由题意可知，，，
，
解得或，
的值为-3或5；
23.解：（1）1，7；
（2）根据表中数据，描点，连线如图所示：
（3）由图可知，①当时；②.
24.解：答案为：10，8；
（2）设铅笔单价为元，橡皮的单价为元，日记本的单价为元，由题意得：
，由①×4-②得，
答：购买2支铅笔、3块橡皮、2本日记本共需17元；
（3）由题意得：
，由①×3-②×2可得：，
.甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
3.6
7.4
8.1
…
0
1
2
3
4
5
6
7
…
…
5
3
-1
1
3
5
…