浙江省杭州市滨江区2023-2024学年下学期八年级数学期末试卷

这是一份浙江省杭州市滨江区2023-2024学年下学期八年级数学期末试卷，共13页。试卷主要包含了 下列说法正确的是等内容，欢迎下载使用。

考生须知:
1. 本试卷满分 120 分, 考试时间 120 分钟.
2. 答题前, 在答题纸指定位置写上学校、班级、姓名、座位号.
3. 必须在答题纸的对应答题位置上答题, 写在其他地方无效. 答题方式详见答题纸上的说明.
4. 如需画图作答, 必须用黑色字迹的钢笔或签字笔将图形线条描黑.
试 题 卷
一. 选择题: 本大题有 10 个小题, 每小题 3 分, 共 30 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的.
1. 2024 年 4 月神舟十八号载人飞船发射成功, 标志着我国在航天领域的加速发展. 下列各航天标志中, 属于中心对称图形的是 ( )

A. B. C. D.
A. 2. 下列化简正确的是 ( )
A. -32=-3 B. 4+9=2+3=5 C. -22=4 D. 29=23
3. 用配方法解方程 x2+x-1=0 时,配方结果正确的是 ( )
A. x+12=2 B. x+122=1 C. x+122=34 D. x+122=54
4. 公安部交管局部署 “一盔一带” 安全守护行动, 某头盔经销商经统计发现某品牌头盔 5 月份销售量 144 个, 7 月份销售量 225 个, 从 5 月份到 7 月份销售量的月增长率相同, 则此月增长率为 ( )
A. 83% B. 69% C. 25% D. 20%
5 某篮球队 5 名场上队员的身高 (单位: cm ) 分别是: 188,190,192,194,195 . 现用一名身高为 190 cm 的队员换下场上身高为 195 cm 的队员,与换人前相比,换人后场上队员的身高
A. 平均数变小, 方差变小 B. 平均数变小, 方差变大
C. 平均数变大, 方差变小 D. 平均数变大, 方差变大
6. 下列说法正确的是 ( )
A. 对角线相等的四边形是矩形 B. 一组对角相等的四边形是平行四边形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直平分且相等的四边形是正方形
7. 用反证法证明 “在直角三角形中,至少有一个锐角不大于 45∘ ” 时,应假设这个直角三角形 ( )
A. 两个锐角都大于 45∘ B. 两个锐角都小于 45∘
C. 两个锐角都等于 45∘ D. 两个锐角都不大于 45∘
8. 已知 x1,y1,x2,y2 为反比例函数 y=-k2+1x 上的两个不同的点,且 x1x2>0 ,则 y2-y1x2-x1 的值是( )
A. 0 B. 正数 C. 负数 D. 非负数
9. 已知关于 x 的函数 y1=kx,y2=bx,y3=kx+bk,b为常数,k≠b且kb≠0 ,则下列说法正确. 的是 ( )
① 函数 y3 与 y1,y2 图象的总交点数至少有两个;
②当 k>-b4 时,函数 y2 和 y3 的图象有两个交点;
③ 当 k=-b4 时,函数 y2 和 y3 的图象只有一个交点;
④ 无论 k,b 取何值, y1 和 y3 始终有两个交点.
A. ①②③④ B. ①②④ C. ①②③ D. ①③④
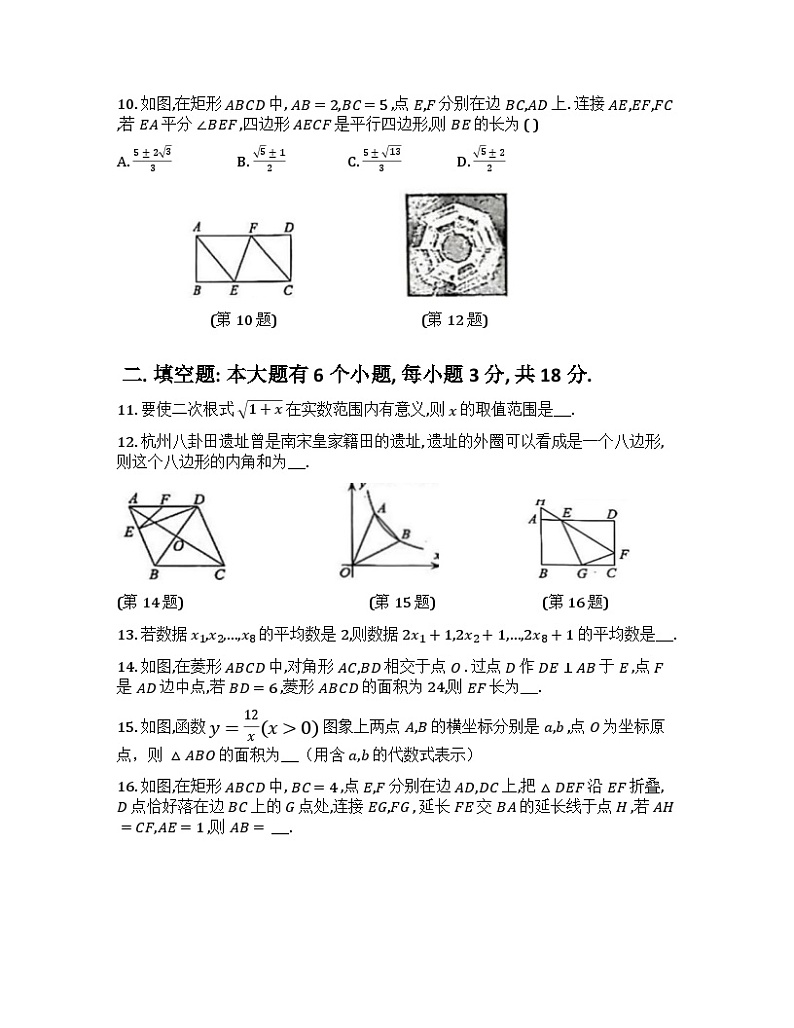
10. 如图,在矩形 ABCD 中, AB=2,BC=5 ,点 E,F 分别在边 BC,AD 上. 连接 AE,EF,FC ,若 EA 平分 ∠BEF ,四边形 AECF 是平行四边形,则 BE 的长为 ( )
A. 5±233 B. 5±12 C. 5±133 D. 5±22

(第 10 题) (第 12 题)
二. 填空题: 本大题有 6 个小题, 每小题 3 分, 共 18 分.
11. 要使二次根式 1+x 在实数范围内有意义,则 x 的取值范围是___.
12. 杭州八卦田遗址曾是南宋皇家籍田的遗址, 遗址的外圈可以看成是一个八边形, 则这个八边形的内角和为___.

(第 14 题) (第 15 题) (第 16 题)
13. 若数据 x1,x2,…,x8 的平均数是 2,则数据 2x1+1,2x2+1,…,2x8+1 的平均数是___.
14. 如图,在菱形 ABCD 中,对角形 AC,BD 相交于点 O . 过点 D 作 DE⊥AB 于 E ,点 F 是 AD 边中点,若 BD=6 ,菱形 ABCD 的面积为 24,则 EF 长为___.
15. 如图,函数 y=12xx>0 图象上两点 A,B 的横坐标分别是 a,b ,点 O 为坐标原点，则 △ABO 的面积为___（用含 a,b 的代数式表示）
16. 如图,在矩形 ABCD 中, BC=4 ,点 E,F 分别在边 AD,DC 上,把△DEF 沿 EF 折叠, D 点恰好落在边 BC 上的 G 点处,连接 EG,FG , 延长 FE 交 BA 的延长线于点 H ,若 AH=CF,AE=1 ,则 AB= ___.
三. 解答题: 本大题有 8 个小题, 共 72 分. 解答应写出文字说明、证明过程或演算步骤.
17. (本题满分 6 分)
计算: (1) 2+3×6 (2) 3-52+20+515
18. (本题满分 6 分)
解方程: (1) x+22=x+2 (2) 2x2-5x+1=0
19. (本题满分 8 分)
某校体操社团共 16 名学生,经测量获得了这 16 名学生的身高 (单位: cm ),数据整理如下:
162,164,165,165,167,168,168,169,170,170,170,171,172,172,174,175
(1) 求这 16 名学生身高的中位数和众数.
（2）从该体操社团中选六名学生参加比赛, 为了使舞台呈现效果更好, 往往选一组学生的身高的方差更小.请你通过计算说明应该选下列甲、乙两组中的哪一组参加比赛?
20. (本题满分 8 分)
如图的网格中, 每个小正方形的边长均为 1 . 仅用无刻度的直尺在给定的网格图中分别按下列要求画图 (保留画图痕迹, 画图过程中辅助线用虚线, 画的最后结果中的线用实线表示)
（1）请在图 1 中画出线段 AB 的中点 C .

图 1 图 2
请把图 2 中的四边形 ABCD 改成一个以 AB 为底边, 面积不变的梯形.
21. (本题满分 10 分)
设函数 y1=k1x ,函数 y2=k2x+bk1,k2,b是常数,k1≠0,k2≠0 .
若函数 y1 和函数 y2 的图象交于点 A2,m,B3,2
(1) 求 m 的值.
（2）求函数 y1,y2 的表达式.
（3）请直接写出当 y1>y2 时, x 的取值范围.
22. (本题满分 10 分)
如图,在 ▱ABCD 中, CA=CD,E 是 AD 的中点,连结 CE 并延长,
交 BA 的延长线于点 F ,连结 DF .
（1）求证: 四边形 AFDC 是菱形.
（2）若 BC=8,AB=5 ,求四边形 DFBC 的面积.
23. (本题满分 12 分)
小江制作了如图一款托盘天平,在天平支点 O 左边托盘 A (固定) 中放置一个物体,在右边托盘 P (可在 BC 上左右移动, OB=10 cm ) 中放置一个可以装水的容器 (容器的质量忽略不计). 在容器中加入一定质量的水,改变托盘 P 与点 O 的距离 x (cm) 10≤x≤40 ,可以使天平左右平衡, 记录天平平衡时容器中加入的水的质量, 得到下表:
（1）①请在所给的平面直角坐标系中作出 y 关于 x 的函数图象. ② 观察函数图象,并求 y 关于 x 的函数表达式.
（2）若在容器中加入的水的质量 y g 满足 7.5≤y≤24 ,
求天平平衡时托盘 P 与点 O 的距离 x cm 的取值范围.
（3）根据杠杆原理,天平平衡时,左盘物体质量 ⋅OA= 右盘物体质量 ⋅OP (不计托盘与横梁质量),其中 OA=8 cm . 小江为了改进托盘天平使得它能在右盘倒入小于 6 g 水时天平也能平衡, 不妨设小江在天平右盘容器中倒入 5 g 水,他准备更换左盘中
的物体,更换的物体质量分别有 35 g,29 g 和 20 g 三款可供选择,保持其他条件不变. 请你通过计算帮助小江从上述三款物体中挑选合适质量的物体,并求此时天平保持平衡时托盘 P 离 O 点的距离.
24. (本题满分 12 分)
如图,在正方形 ABCD 中,点 E,F 分别在边 AB 和 BC 的延长线上(点 E 不与点 A ,点 B 重合),且 CF=AE ,连接 DE,DF,EF . 过点 D 作 DH⊥EF 于 H ,连接 CH .
（1）求证: 点 H 是线段 EF 的中点.
（2）若 AB=3,CF=1 ,求 CH .
（3）求证: 点 H 始终在正方形 ABCD 的对角线 AC 上.
答案
C
D
D
C
A
D
A
C
A
C
X≥ -1
1080°
5
2.5
6(a²+b²）ab
22
17.
12+3×6
=2×6+3×6
=12+18
=23+32
23-52+20+515
=9+5-65+25+5
=14-35 .
18.(1) x+22=x+2 ,
x+22-x+2=0
x+2x+1=0
则 x+2=0 或 x+1=0 ,
所以 x1=-1,x2=-2 .
(2)因为 a=2 ， b=-5 ， c=1 ，
所以 Δ=-52-4×2×1=17>0 ,
则 x=5±174 ,
所以 x1=5+174,x2=5-174 .
19.（1）这16名学生身高的中位数为
169+1702=169.5 cm ，众数为 170 cm ；
(2) 甲组数据的平均数为
16×162+164+165+165+169+171=
166 cm
，乙组数据的平均数为
16×167+168+170+172+174+175=
171cm
,
所以甲组数据的方差为
16×[162-1662+164-1662+2×
165-1662+169-1662+171-1662]=
283
乙组数据的方差为
16×167-1712+168-1712+
170-1712+172-1712+174-1712+
175-1712]=263
,
∵263<283
∴ 应该选乙组参加比赛.
20.解; (1)如图1中，点 C 即为所求;
图 1 图 2
如图2中，四边形 ABCG 即为所求.
21.（1）由题意， ∵B3,2 在函数 y1=k1x 上，
∴k1=3×2=6 .
∴y1=6x .
又 A2,m 在函数 y1=6x 上，
∴2m=6 .
∴m=3 .
2 由题意，根据（1）得， y1=6x ， A2,3 ，
又 B3,2 ，
∴2k2+b=33k2+b=2 .
∴k2=-1b=5.
∴y2=-x+5 .
3 由题意，在同一坐标系中画出 y1=6x 和
y2=-x+5 的图象如下，
∵ 当 y1>y2 时， x 的取值范围即为反比例函数的图象在一次函数图象上方时对应的自变量的取值范围，
又 A2,3,B3,2 ,
∴ 当 y1>y2 时， 03 .
22.1 证明： ∵AC=CD ， E 是 AD 的中点，
∴∠ACE=∠DCE ,
∵ 四边形 ABCD 是平行四边形，
∴AB//CD ,
即 AF//CD ,
∴∠DCF=∠AFC ,
∴∠ACE=∠AFE ,
∴AC=AF ,
∴AF=CD ,
∴ 四边形 AFDC 是平行四边形，
∵AC=CD ,
∴ 四边形 AFDC 是菱形.
2∵ 四边形 ABCD 是平行四边形，
∴CD=AB=5 ， AD=BC=8 ，
∵ 四边形 AFDC 是菱形,
∴CF⊥AD .
∴DE=12AD=4 ,
∴CE=CD2-DE2=3 ，
∴CF=2CE=6 ,
∴ 四边形 DFBC 的面积
=12CF⋅AD=12×6×8=24 .
（1） y1=240x （x＞0）
（2）10≤ x ≤ 32
（3）240÷8=30
5×40÷8=25
5×10÷8=6.25
6.25≤ 质量 ≤25 ，即选20g
(1)证明如下：△ADE≅△CDF（SAS）∴△DEF是等腰三角形
∵过点 D 作 DH⊥EF 于 H
∴点 H 是线段 EF 的中点.
（2）过点 H 作 MH⊥BF 于 M
HM为△EBF的中位线，
∴HM=1，CM=1
∴△HMC是等腰直角三角形
∴CH=2
（3）由（2）知△HMC是等腰直角三角形
∴∠HCM=45°
即点 H 始终在正方形 ABCD 的对角线 AC 上
甲组学生的身高
162
164
165
165
169
171
乙组学生的身高
167
168
170
172
174
175
托盘 P 与点 O 的距离 x/cm
40
24
20
16
12
10
加入的水的质量 y /g
6
10
12
15
20.1
24