沪教版暑假新九年级数学考点讲与练第04讲相似三角形中的“8”字模型(考点讲与练)(原卷版+解析)

这是一份沪教版暑假新九年级数学考点讲与练第04讲相似三角形中的“8”字模型(考点讲与练)(原卷版+解析)，共18页。
8字_平行型
条件：CD∥AB,
结论：ΔPAB∼ΔPCD(上下相似);
左右不一定相似,不一定全等，但面积相等;
四边形ABCD为一般梯形.
条件：CD∥AB,PD=PC.
结论：ΔPAB∼ΔPCD∼ΔPDC(上下相似)
ΔPAD≅ΔPBC左右全等；
四边形ABCD为等腰梯形；
8字_不平行型
条件：∠CDP=∠BAP.
结论：
ΔAPB∼ΔDPC(上下相似);
ΔAPD∼ΔBPC(左右相似);
【考点剖析】
一．选择题（共2小题）
1．(2023秋•静安区期末）已知点D、E分别在△ABC的边AB、AC的反向延长线上，且ED∥BC，如果AD：DB＝1：4，ED＝2，那么边BC的长是（ ）
A．8B．10C．6D．4
2．(2023秋•浦东新区校级期末）如图，∠BEC＝∠CDB，下列结论正确的是（ ）
A．EF•BF＝DF•CFB．BE•CD＝BF•CF
C．AE•AB＝AD•ACD．AE•BE＝AD•DC
二．填空题（共2小题）
3．(2023春•徐汇区校级期中）如图，请添加一个条件使AB∥CD，这条件可以是 ．
4．(2023秋•青浦区期末）如图，在矩形ABCD中，∠BCD的角平分线CE与边AD交于点E，∠AEC的角平分线与边CB的延长线交于点G，与边AB交于点F，如果AB=32，AF＝2BF，那么GB＝ ．
三．解答题（共1小题）
5．(2023春•杨浦区校级期中）如图1，在△ABC中，点E在AC的延长线上，且∠E＝∠ABC．
（1）求证：AB2＝AC•AE；
（2）如图2，D在BC上且BD＝3CD，延长AD交BE于F，若ABAC=32，求CDEF的值．
【过关检测】
1．(2023·上海·九年级专题练习）如图，在矩形ABCD中， AB=3，BC=4，将矩形ABCD绕点C旋转，点A、B、D的对应点分别为A’ 、B’、 D’，当A’ 落在边CD的延长线上时，边A’ D’ 与边 AD的延长线交于点F，联结CF，那么线段CF的长度为____．
2．(2023·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．
（1）求证：△BND∽△CNM；
（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．
3．(2023·上海·九年级期末）如图，在平行四边形ABCD中，BC=8，点E、F是对角线BD上的两点，且BE=EF=FD，AE的延长线交BC于点G，GF的延长线交AD于点H．
（1）求HD的长；
（2）设的面积为a，求四边形AEFH的面积．（用含a的代数式表示）
4．(2023·上海奉贤·二模）已知：如图，在梯形ABCD中，CD∥AB，∠DAB＝90°，对角线AC、BD相交于点E，AC⊥BC，垂足为点C，且BC2＝CE•CA．
（1）求证：AD＝DE；
（2）过点D作AC的垂线，交AC于点F，求证：CE2＝AE•AF．
第04讲 相似三角形中的“8”字模型（核心考点讲与练）
【基础知识】
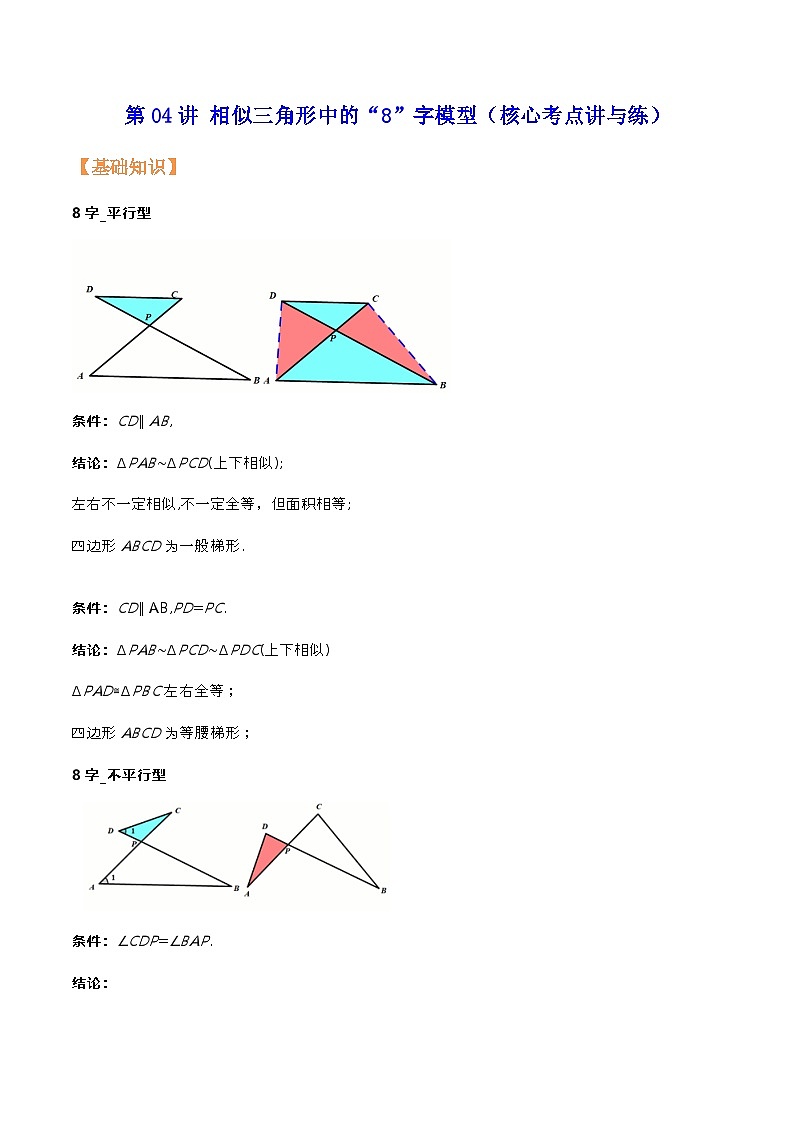
8字_平行型
条件：CD∥AB,
结论：ΔPAB∼ΔPCD(上下相似);
左右不一定相似,不一定全等，但面积相等;
四边形ABCD为一般梯形.
条件：CD∥AB,PD=PC.
结论：ΔPAB∼ΔPCD∼ΔPDC(上下相似)
ΔPAD≅ΔPBC左右全等；
四边形ABCD为等腰梯形；
8字_不平行型
条件：∠CDP=∠BAP.
结论：
ΔAPB∼ΔDPC(上下相似);
ΔAPD∼ΔBPC(左右相似);
【考点剖析】
一．选择题（共2小题）
1．(2023秋•静安区期末）已知点D、E分别在△ABC的边AB、AC的反向延长线上，且ED∥BC，如果AD：DB＝1：4，ED＝2，那么边BC的长是（ ）
A．8B．10C．6D．4
分析：根据相似三角形的判定定理得出△EAD∽△CAB，根据相似三角形的性质求出即可．
【解答】解：如图，
∵DE∥BC，
∴△EAD∽△CAB，
∴EDBC=ADAB，
∵ADDB=14，DE＝2，
∴ADAB=13，
∴2BC=13，
∴BC＝6．
故选：C．
【点评】本题考查了相似三角形的性质和判定的应用，能推出△EAD∽△CAB是解此题的关键．
2．(2023秋•浦东新区校级期末）如图，∠BEC＝∠CDB，下列结论正确的是（ ）
A．EF•BF＝DF•CFB．BE•CD＝BF•CF
C．AE•AB＝AD•ACD．AE•BE＝AD•DC
分析：结合图形利用8字模型相似三角形证明△EFB∽△DFC，然后利用等角的补角相等得出∠AEC＝∠ADB，最后证明△ABD∽△ACE，利用相似三角形的对应边成比例逐一判断即可．
【解答】解：∵∠BEC＝∠CDB，∠EFB＝∠DFC，
∴△EFB∽△DFC，
∴EFDF=FBFC，
∴EF•FC＝DF•FB，
故A不符合题意：
∵△EFB∽△DFC，
∴BECD=BFFC，
∴BE•CF＝CD•BF，
故B不符合题意；
∵∠BEC＝∠CDB，∠BEC+∠AEC＝180°，∠BDC+∠ADB＝180°，
∴∠AEC＝∠ADB，
∴△ABD∽△ACE，
∴ABAC=ADAE，
∴AB•AE＝AD•AC，
故C符合题意；
因为：AE，BE，AD，CD组不成三角形，也不存在比例关系，
故D不符合题意；
故选：C．
【点评】本题考查了相似三角形的判定与性质，根据题目的已知条件并结合图形分析是解题的关键．
二．填空题（共2小题）
3．(2023春•徐汇区校级期中）如图，请添加一个条件使AB∥CD，这条件可以是 ∠BAC＝∠DCA或∠ABD＝∠CDB或∠BAD+∠CDA＝180°或∠ABC+∠DCB＝180° ．
分析：利用平行线的判定定理找出内错角和同旁内角的满足条件即可．
【解答】解：∵内错角相等，两直线平行，
∴当∠BAC＝∠DCA或∠ABD＝∠CDB时，AB∥CD．
∵同旁内角互补，两直线平行，
∴当∠BAD+∠CDA＝180°或∠ABC+∠DCB＝180°时，AB∥CD．
综上所述，添加一个条件使AB∥CD，这条件可以是：
∠BAC＝∠DCA或∠ABD＝∠CDB或∠BAD+∠CDA＝180°或∠ABC+∠DCB＝180°，
故答案为：∠BAC＝∠DCA或∠ABD＝∠CDB或∠BAD+∠CDA＝180°或∠ABC+∠DCB＝180°．
【点评】本题主要考查了平行线的判定与性质，充分利用平行线的判定法则是解题的关键．
4．(2023秋•青浦区期末）如图，在矩形ABCD中，∠BCD的角平分线CE与边AD交于点E，∠AEC的角平分线与边CB的延长线交于点G，与边AB交于点F，如果AB=32，AF＝2BF，那么GB＝ 2−2 ．
分析：证明△AFE∽△BFG，得AE＝2BG，设BG＝a，则AE＝2a，根据平行线的性质和角平分线的定义可得CD＝DE＝AB＝32，CE＝CG=2CD=2×32=6，从而得结论．
【解答】解：∵四边形ABCD是矩形，
∴AD∥BC，
∴△AFE∽△BFG，
∴AFBF=AEBG，
∵AF＝2BF，
∴AE＝2BG，
设BG＝a，则AE＝2a，
∵CE平分∠DCB，EF平分∠AEC，
∴∠DCE＝∠ECB，∠AEF＝∠CEF，
∵AD∥CG，
∴∠AEF＝∠G，∠DEC＝∠ECG，
∴∠CEF＝∠G，∠DEC＝∠DCB，
∴CD＝DE＝AB＝32，CE＝CG=2CD=2×32=6，
∴a+2a+32=6，
∴a＝2−2，
∴GB＝2−2．
故答案为：2−2．
【点评】本题考查了矩形的性质的运用，相似三角形的判定及性质的运用，勾股定理的运用，等腰三角形的性质和判定的运用，解答时运用角平分线的定义和平行线得等腰是本题的关键．
三．解答题（共1小题）
5．(2023春•杨浦区校级期中）如图1，在△ABC中，点E在AC的延长线上，且∠E＝∠ABC．
（1）求证：AB2＝AC•AE；
（2）如图2，D在BC上且BD＝3CD，延长AD交BE于F，若ABAC=32，求CDEF的值．
分析：（1）利用两角相等的两个三角形相似，证明△ABC∽△AEB，然后利用相似三角形的性质即可解答；
（2）过点E作EH∥CB，交AF的延长线于点H，利用（1）的结论可得ABAE=ACAB=BCEB=23，先AC＝2a，AB＝3a，从而求出AE的长，进而求出ACAE的值，再根据已知设CD＝m，BD＝3m，从而求出BC，BE的长，然后证明A字模型相似三角形△ACD∽△AEH，利用相似三角形的性质可得EH=94m，再证明8字模型相似三角形△BDF∽△EHF，利用相似三角形的性质可得BFEF=43，从而求出EF的长，进行计算即可解答．
【解答】（1）证明：∵∠E＝∠ABC，∠A＝∠A，
∴△ABC∽△AEB，
∴ABAE=ACAB，
∴AB2＝AC•AE；
（2）解：过点E作EH∥CB，交AF的延长线于点H，
∵△ABC∽△AEB，
∴ABAE=ACAB=BCEB=23，
∴设AC＝2a，AB＝3a，
∴3aAE=23，
∴AE=92a，
∴ACAE=2a92a=49，
∵BD＝3CD，
∴设CD＝m，则BD＝3m，
∴BC＝CD+BD＝4m，
∴4mEB=23，
∴EB＝6m，
∵EH∥CD，
∴∠ACD＝∠AEH，∠ADC＝∠AHE，
∴△ACD∽△AEH，
∴ACAE=CDEH=49，
∴EH=94m，
∵EH∥BD，
∴∠BDF＝∠DHE，∠DBF＝∠FEH，
∴△BDF∽△EHF，
∴BFEF=BDEH=3m94m=43，
∴EF=37BE=187m，
∴CDEF=m187m=718，
∴CDEF的值为718．
【点评】本题考查了相似三角形的判定与性质，平行线分线段成比例，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
【过关检测】
题型二：（双）8型相似
1．(2023·上海·九年级专题练习）如图，在矩形ABCD中， AB=3，BC=4，将矩形ABCD绕点C旋转，点A、B、D的对应点分别为A’ 、B’、 D’，当A’ 落在边CD的延长线上时，边A’ D’ 与边 AD的延长线交于点F，联结CF，那么线段CF的长度为____．
答案:
分析：由勾股定理可求A'C=5，可得A'D= A'C-CD=2，由△ECD∽△A'CB'，对应边成比例即可求出DE的长，再由△A'DF∽△CDE求出DF的长，最后在Rt△DFC中由勾股定理即可求出DF.
【详解】解：由旋转前后对应边相等可知：A'B'=AB=3，B'C=BC=4
∴由勾股定理可知：A'C=，
∴A'D= A'C-CD=2，
又∠ADC=∠B'=90°，且∠ECD=∠A'CB'，
∴△ECD∽△A'CB'，
∴，代入数据：，
∴，
又A'F∥CE，
∴∠CED=∠A'FD，且∠EDC=∠FDA'，
∴△A'DF∽△CDE，
，代入数据：，
∴，
在Rt△DFC中由勾股定理可知：
.
故答案为：.
【点睛】本题借助矩形的性质考查了相似三角形的性质和判定，熟练掌握相似三角形的性质和判定是解决此题的关键.
2．(2023·上海市奉贤区古华中学九年级期中）已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．
（1）求证：△BND∽△CNM；
（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．
分析：（1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；
（2）先利用AD2=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=∠4，∠2=∠3，所以∠3=∠4，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．
【详解】证明：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
而BE=AB，
∴BE=CD，
而BE∥CD，
∴四边形BECD为平行四边形，
∴BD∥CE，
∵CM∥DB，
∴△BND∽△CNM；
（2）∵AD2=AB•AF，
∴AD：AB=AF：AD，
而∠DAB=∠FAD，
∴△ADB∽△AFD，
∴∠1=∠F，
∵CD∥AF，BD∥CE，
∴∠F=∠4，∠2=∠3，
∴∠3=∠4，
而∠NMC=∠CMD，
∴△MNC∽△MCD，
∴MC：MD=CN：CD，
∴MC•CD=MD•CN，
而CD=AB，
∴CM•AB=DM•CN．
【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．
3．(2023·上海·九年级期末）如图，在平行四边形ABCD中，BC=8，点E、F是对角线BD上的两点，且BE=EF=FD，AE的延长线交BC于点G，GF的延长线交AD于点H．
（1）求HD的长；
（2）设的面积为a，求四边形AEFH的面积．（用含a的代数式表示）
答案:（1）2；（2）
分析：（1）根据平行四边形的性质得，根据相似三角形的判定得，，由BE=EF=FD可得出，，根据相似三角形的性质即可求解；
（2）由BE=EF可得与的面积相等，根据相似三角形的面积比等于相似比的平方可得与的值，-即可得四边形AEFH的面积．
【详解】解：（1）∵平行四边形ABCD，BC=8，
∴，=8，
∴，，
∴，，
∵BE=EF=FD，
∴，，
∴BG=AD=4，HD=BG，
∴HD=2；
（2）∵BE=EF，
∴=a，
∴，
∵，，，，
∴，，
∴四边形AEFH的面积=-=．
【点睛】本题考查平行四边形的性质，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
4．(2023·上海奉贤·二模）已知：如图，在梯形ABCD中，CD∥AB，∠DAB＝90°，对角线AC、BD相交于点E，AC⊥BC，垂足为点C，且BC2＝CE•CA．
（1）求证：AD＝DE；
（2）过点D作AC的垂线，交AC于点F，求证：CE2＝AE•AF．
分析：（1）根据相似三角形的判定定理得到△BCE∽△ACB，根据相似三角形的性质得到∠CBE＝∠CAB，根据等角的余角相等得到∠BEC＝∠DAE，根据等腰三角形的判定定理证明；
（2）根据平行线分线段成比例定理得到， ，得到，整理得到 CE2＝AE•EF，根据等腰三角形的三线合一得到AF＝EF，证明结论．
【详解】
证明：（1）∵BC2＝CE•CA，
∴，又∠ECB＝∠BCA，
∴△BCE∽△ACB，
∴∠CBE＝∠CAB，
∵AC⊥BC，∠DAB＝90°，
∴∠BEC+∠CBE＝90°，∠DAE+∠CAB＝90°，
∴∠BEC＝∠DAE，
∵∠BEC＝∠DEA，
∴∠DAE＝∠DEA，
∴AD＝DE；
（2）过点D作AC的垂线，交AC于点F，如图，
∵DF⊥AC，AC⊥BC，
∴∠DFE＝∠BCA＝90°，
∴DF∥BC，
∴，
∵DC∥AB，
∴，
∴，
∴CE2＝AE•EF，
∵AD＝DE，DF⊥AC，
∴AF＝EF，
∴CE2＝AE•AF．
【点睛】本题考查的是相似三角形的判定和性质、直角梯形的概念，掌握相似三角形的判定定理和性质定理是解题的关键．