沪教版暑假新九年级数学考点讲与练第07讲相似三角形中“一线三等角”问题(考点讲与练)(原卷版+解析)

这是一份沪教版暑假新九年级数学考点讲与练第07讲相似三角形中“一线三等角”问题(考点讲与练)(原卷版+解析)，共25页。
一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。或叫 “K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：
当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。
一般类型：
基本类型：
同侧“一线三等角” 异侧“一线三等角”
【考点剖析】
1．(2023秋•浦东新区期末）如图，a∥b∥c，直线a与直线b之间的距离为，直线c与直线b之间的距离为2，等边△ABC的三个顶点分别在直线a、直线b、直线c上，则等边三角形的边长是 ．
2．(2023秋•冠县期末）已知：如图，△ABC是等边三角形，点D、E分别在边BC、AC上，∠ADE＝60°．
（1）求证：△ABD∽△DCE；
（2）如果AB＝3，EC＝，求DC的长．
分析：（1）△ABC是等边三角形，得到∠B＝∠C＝60°，AB＝AC，推出∠BAD＝∠CDE，得到△ABD∽△DCE；
（2）由△ABD∽△DCE，得到＝，然后代入数值求得结果．
3.(2023浦东新区二模）已知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE上CF＝CD，过点F作FG⊥FC交AD于点G．
（1）求证：GF＝GD；
（2）联结AF，求证：AF⊥DE．
整体分析：
根据等角的余角相等得到即可证明.
联结CG.证明△DAE≌△CDG,得到.进而得到，根据等边对等角得到根据三角形的内角和可以求出∠AFD= 90°，即可证明.
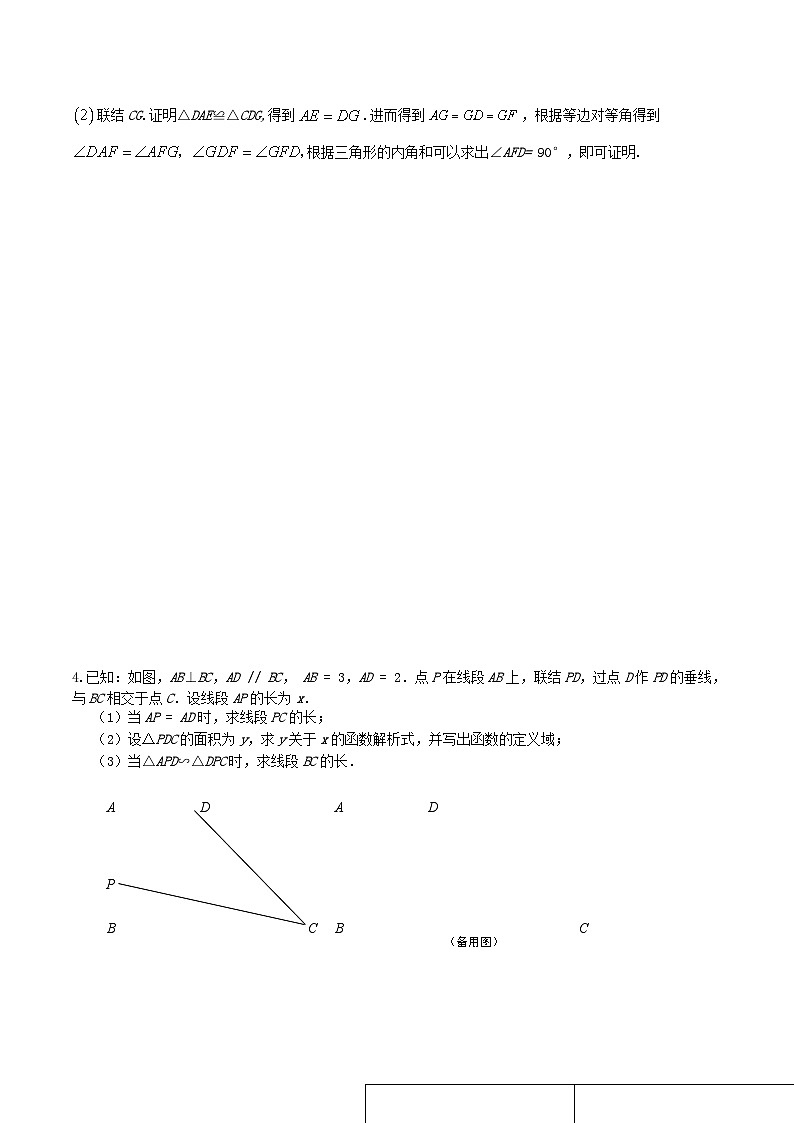
4.已知：如图，AB⊥BC，AD // BC， AB = 3，AD = 2．点P在线段AB上，联结PD，过点D作PD的垂线，与BC相交于点C．设线段AP的长为x．
（1）当AP = AD时，求线段PC的长；
（2）设△PDC的面积为y，求y关于x的函数解析式，并写出函数的定义域；
（3）当△APD∽△DPC时，求线段BC的长．
A
B
C
D
P
A
B
C
D
（备用图）
【过关检测】
1．(2023·上海市育才初级中学九年级阶段练习）如图，在边长为6的正方形ABCD中，点E为AD边上的一个动点(与点A、D不重合)，∠EBM=45°，BE交对角线AC于点F，BM交对角线AC于点G、交CD于点M．
（1）如图1，联结BD，求证：△DEB∼△CGB，并写出的值；
（2）联结EG，如图2，若设，求y关于的函数解析式，并写出函数的定义域；
（3）当M为边DC的三等分点时，求的面积．
2．(2023·上海宝山·九年级阶段练习）如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．
（1）求证：AB·AF＝CB·CD；
（2）已知AB＝15 cm，BC＝9 cm，P是射线DE上的动点．设DP＝x cm（），四边形BCDP的面积为y cm2．
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值．
3．(2023·上海·九年级专题练习）（1）正方形中，对角线与相交于点，如图1，请直接猜想并写出与之间的数量关系：________；
（2）如图2，将（1）中的绕点逆时针旋转得到，连接，，请猜想线段与的数量关系，并证明你的猜想；
（3）如图3，矩形和有公共顶点，且，，则________．
4.如图，在中，，，，点D是BC的中点，点E是AB边上的动点，交射线AC于点F．
（1）求AC和BC的长；（2分）
（2）当∥时，求的长；（5分）
（3）联结，当和相似时，求的长．（7分）
5.在梯形ABCD中,AD∥BC，.（如图1）
(1)试求的度数；
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.（如图2）
①求证:∽；
②试判断的形状（从边、角两个方面考虑），并加以说明；
③设,试求关于的函数解析式,并写出定义域.
第07讲 相似三角形中“一线三等角”问题（核心考点讲与练）
【基础知识】
一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。或叫 “K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：
当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。
一般类型：
基本类型：
同侧“一线三等角” 异侧“一线三等角”
【考点剖析】
1．(2023秋•浦东新区期末）如图，a∥b∥c，直线a与直线b之间的距离为，直线c与直线b之间的距离为2，等边△ABC的三个顶点分别在直线a、直线b、直线c上，则等边三角形的边长是 2 ．
分析：过点A作AD⊥直线b于D，将△ABD绕点A逆时针旋转60°得到△ACE，作EG⊥直线c于G交直线a于F．想办法求出AE，EC即可解决问题．
【解答】解：如图，过点A作AD⊥直线b于D，将△ABD绕点A逆时针旋转60°得到△ACE，作EG⊥直线c于G交直线a于F．
则有∠AEC＝∠ADB＝∠AFE＝∠EGC＝90°，AE＝AD＝，∠EAF＝∠CEG＝30°，
∴EF＝AE＝，
∴EG＝，CG＝EG＝，CE＝2CG＝5，
∴AC＝＝＝2．
∴等边△ABC的边长为2．
故答案为：2．
【点评】本题考查了相似三角形的性质与判定，勾股定理的运用，直角三角形的性质的运用，相似三角形的性质的运用，解答时构造相似三角形是关键．
2．(2023秋•冠县期末）已知：如图，△ABC是等边三角形，点D、E分别在边BC、AC上，∠ADE＝60°．
（1）求证：△ABD∽△DCE；
（2）如果AB＝3，EC＝，求DC的长．
分析：（1）△ABC是等边三角形，得到∠B＝∠C＝60°，AB＝AC，推出∠BAD＝∠CDE，得到△ABD∽△DCE；
（2）由△ABD∽△DCE，得到＝，然后代入数值求得结果．
【解答】（1）证明：∵△ABC是等边三角形，
∴∠B＝∠C＝60°，AB＝AC，
∵∠B+∠BAD＝∠ADE+∠CDE，∠B＝∠ADE＝60°，
∴∠BAD＝∠CDE
∴△ABD∽△DCE；
（2）解：由（1）证得△ABD∽△DCE，
∴＝，
设CD＝x，则BD＝3﹣x，
∴＝，
∴x＝1或x＝2，
∴DC＝1或DC＝2．
【点评】本题考查了等边三角形的性质，相似三角形的判定和性质，注意数形结合和方程思想的应用．
3.(2023浦东新区二模）已知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE上CF＝CD，过点F作FG⊥FC交AD于点G．
（1）求证：GF＝GD；
（2）联结AF，求证：AF⊥DE．
整体分析：
根据等角的余角相等得到即可证明.
联结CG.证明△DAE≌△CDG,得到.进而得到，根据等边对等角得到根据三角形的内角和可以求出∠AFD= 90°，即可证明.
满分解答：
∵四边形是正方形，∴,
∵FG⊥FC， ∴∠GFC= 90°,
∵ ∴∠CDF=∠CFD ,
∴∠GFC-∠CFD=∠ADC-∠CDE，即∠GFD=∠GDF.
∴GF=GD.
联结CG.
∵ ∴点在线段的中垂线上,
∴GC⊥DE，
∴∠CDF+∠DCG= 90°，
∵∠CDF+∠ADE= 90°，
∴∠DCG=∠ADE
四边形是正方形,
∴AD=DC，∠DAE=∠CDG= 90°，
∴△DAE≌△CDG,
∴.
点是边的中点，
点是边的中点，
∴,
∴
∵
∴
∴∠AFD= 90°，即AF⊥DE.
点睛：属于四边形的综合题，考查了正方形的性质，全等三角形的判定与性质，等腰三角形的判定与性质等，考查知识点比较多，难度不大，熟练掌握各个知识点是解题的关键.
4.已知：如图，AB⊥BC，AD // BC， AB = 3，AD = 2．点P在线段AB上，联结PD，过点D作PD的垂线，与BC相交于点C．设线段AP的长为x．
（1）当AP = AD时，求线段PC的长；
（2）设△PDC的面积为y，求y关于x的函数解析式，并写出函数的定义域；
（3）当△APD∽△DPC时，求线段BC的长．
A
B
C
D
P
A
B
C
D
（备用图）
满分解答：
（1）过点C作CE⊥AD，交AD的延长线于点E．
∵ AB⊥BC，CE⊥AD，PD⊥CD，AD // BC，
∴ ∠ABC =∠AEC =∠PDC = 90°，
CE = AB = 3．
∵ AD // BC，∴ ∠A +∠ABC = 180°．即得 ∠A = 90°．
又∵ ∠ADC =∠DCE +∠DEC，∠ADC =∠ADP +∠PDC，
∴ ∠ADP =∠DCE．
又由 ∠A =∠DEC = 90°，得 △APD∽△DCE．
∴ ．
于是，由AP = AD = 2，得 DE = CE = 3．…………………………（2分）
在Rt△APD和Rt△DCE中，
得 ，．…………………………………………（1分）
于是，在Rt△PDC中，得 ． （1分）
（2）在Rt△APD中，由 AD = 2，AP = x，
得 ．……………………………………………………（1分）
∵ △APD∽△DCE，∴ ．
∴ ．…………………………………………（1分）
在Rt△PCD中，．
∴ 所求函数解析式为．…………………………………（2分）
函数的定义域为 0 < x ≤ 3．…………………………………………（1分）
（3）当△APD∽△DPC时，即得 △APD∽△DPC∽△DCE．…………（1分）
根据题意，当△APD∽△DPC时，有下列两种情况：
（ⅰ）当点P与点B不重合时，可知 ∠APD =∠DPC．
由 △APD∽△DCE，得 ．即得 ．
由 △APD∽△DPC，得 ．
∴ ．即得 DE = AD = 2．
∴ AE = 4．
易证得四边形ABCE是矩形，∴ BC = AE = 4．…………………（2分）
（ⅱ）当点P与点B重合时，可知 ∠ABD =∠DBC．
在Rt△ABD中，由 AD = 2，AB = 3，得 ．
由 △ABD∽△DBC，得 ．
即得 ．
解得 ．………………………………………………………（2分）
∴ △APD∽△DPC时，线段BC的长分别为4或．
方法总结
本题重点在于：过点C作CE⊥AD，交AD的延长线于点E．(构造一线三角，出现相似三角形，进行求解)
【过关检测】
1．(2023·上海市育才初级中学九年级阶段练习）如图，在边长为6的正方形ABCD中，点E为AD边上的一个动点(与点A、D不重合)，∠EBM=45°，BE交对角线AC于点F，BM交对角线AC于点G、交CD于点M．
（1）如图1，联结BD，求证：△DEB∼△CGB，并写出的值；
（2）联结EG，如图2，若设，求y关于的函数解析式，并写出函数的定义域；
（3）当M为边DC的三等分点时，求的面积．
答案:；；或
分析：（1）根据正方形的性质得到∠EDB＝∠GCB＝45°，∠ABD＝∠CBD＝45°，根据相似三角形的判定定理证明即可；
（2）作EH⊥AC于H，根据等腰直角三角形的性质、勾股定理和相似三角形的性质得到y关于x的函数解析式；
（3）分CM＝CD和CM＝CD两种情况，根据相似三角形的性质解答即可．
【详解】（1）证明：∵四边形ABCD是正方形，
∴∠EDB＝∠GCB＝45°，∠ABD＝∠CBD＝45°，又∠EBM＝45°，
∴∠GBC＋∠DBM＝45°，∠EBD＋∠DBM＝45°，
∴∠GBC＝∠EBD，又∠EDB＝∠GCB＝45°，
∴△DEB∽△CGB，
∴DE：CG＝BD：BC＝；
（2）如图2，作EH⊥AC于H，
则AH＝EH＝x，
∵△DEB∽△CGB，
∴，
∴CG＝（6−x），
∴HG＝AC−AH−CG＝3，
∵EG2＝EH2＋HG2，
∴；
（3）当CM＝CD＝2时，
∵四边形ABCD是正方形，
∴CD∥AB，
∴，
∴CG＝，
∴DE＝3，则AE＝3，
∴AH＝EH＝，
∵AD∥BC，
∴，
∴AF＝2，
∴GF＝AC−AF−CG＝，
∴S△EGF＝×FG×EH＝，
当CM＝CD＝4时，
，
∴CG＝，
∴DE＝，则AE＝，
AH＝EH＝，
∵，
∴AF＝，
∴GF＝AC−AF−CG＝，
∴S△EGF＝×FG×EH＝．
综上,S△EGF=或
【点睛】本题考查相似三角形的判定和性质的应用、正方形的性质的应用，正确作出辅助线、灵活运用相关的定理是解题的关键，注意分情况讨论思想的运用．
2．(2023·上海宝山·九年级阶段练习）如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．
（1）求证：AB·AF＝CB·CD；
（2）已知AB＝15 cm，BC＝9 cm，P是射线DE上的动点．设DP＝x cm（），四边形BCDP的面积为y cm2．
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值．
答案:（1）见解析；（2）①（）；②当时，△PBC的周长最小，此时．
分析：（1）由已知条件易证△DCF∽△ABC，可得，即可得AB·AF＝CB·CD；
（2）①由勾股定理求得AC=12，即可得CF＝AF＝6，根据四边形BCDP的面积=△DCP的面积+△BCP的面积即可得y关于x的函数关系式；
②由题意可知△PBC的周长最小，就是PB＋PC最小，当当P、A、B三点共线时PB＋PA最小．这时求得x、y的值即可．
【详解】（1）证明：∵AD＝CD，DE⊥AC，
∴DE垂直平分AC
∴AF＝CF，∠DFA＝∠DFC＝90°，∠DAF＝∠DCF．
∵∠DAB＝∠DAF＋∠CAB＝90°，∠CAB＋∠B＝90°，
∴∠DCF＝∠DAF＝∠B
在Rt△DCF和Rt△ABC中，
∠DFC＝∠ACB＝90°，∠DCF＝∠B
∴△DCF∽△ABC
∴，即．
∴AB·AF＝CB·CD
（2）解①∵AB＝15 BC＝9 ∠ACB＝90°
∴AC＝＝＝12
∴CF＝AF＝6
∴y=（x+9）×6＝3x＋27（x＞0）
②∵BC＝9（定值），
∴△PBC的周长最小，就是PB＋PC最小．
由（1）可知，点C关于直线DE的对称点是点A，
∴PB＋PC＝PB＋PA，故只要求PB＋PA最小．
显然当P、A、B三点共线时PB＋PA最小．
此时DP＝DE，PB＋PA＝AB．
由（1），∠ADF＝∠FAE，∠DFA＝∠ACB＝90°，得△DAF∽△ABC．
由EF∥BC，得AE＝BE＝AB＝，EF＝．
∴AF∶BC＝AD∶AB，
即6∶9＝AD∶15．
∴AD＝10．
Rt△ADF中，AD＝10，AF＝6，∴DF＝8．
∴DE＝DF＋FE＝8＋＝．
∴当x＝时，△PBC的周长最小，此时y＝
3．(2023·上海·九年级专题练习）（1）正方形中，对角线与相交于点，如图1，请直接猜想并写出与之间的数量关系：________；
（2）如图2，将（1）中的绕点逆时针旋转得到，连接，，请猜想线段与的数量关系，并证明你的猜想；
（3）如图3，矩形和有公共顶点，且，，则________．
答案:（1）AO＝CD；（2），见解析；（3）
分析：(1)根据正方形的性质可得，,由锐角三角比可得AO与CD的关系；
(2)由正方形性质可得，△ABC和△OBC都是等腰直角三角形，得,由旋转可得BC1＝BO1，易证△BDC1∽△BAO1,可得，即;
(3)由∠EBF＝∠ABD＝30°，运用锐角三角比可得，易证∠EBA＝∠FBD，可得△AEB∽△FBD，即.
【详解】
解：(1) ∵四边形ABCD为正方形，
∴,
∴AO＝CD．
(2) 如图2，
∵四边形ABCD为正方形，
∴AB＝BC，AC＝BD，OB＝OC，∠OBC＝∠ABO＝45°，∠BOC＝90°，
∴△ABC和△OBC都是等腰直角三角形，
∴，，
∴，
∵△BOC绕点B逆时针方向旋转得到△BO1C1，
∴∠O1BC1＝∠OBC＝45°，OB＝O1B，BC1＝BC，
∴BC1＝BO1，
∵∠1+∠3＝45°，∠2+∠3＝45°，
∴∠1＝∠2，
∴△BDC1∽△BAO1
∴，
∴
(3) 如图3 在Rt△EBF中，cs∠EBF＝
在Rt△ABD中，cs∠ABD＝，
∵∠EBF＝∠ABD＝30°，
∴，
∵∠EBF+∠FBA＝∠ABD+∠FBA，
即∠EBA＝∠FBD，
∴△AEB∽△FBD，
∴.
【点睛】本题考查了正方形的性质，锐角三角比以及相似三角形的判定与性质，较为综合，熟练分析图形，寻找相等的角与相似三角形是解题的关键.
4.如图，在中，，，，点D是BC的中点，点E是AB边上的动点，交射线AC于点F．
（1）求AC和BC的长；（2分）
（2）当∥时，求的长；（5分）
（3）联结，当和相似时，求的长．（7分）
答案：
（1）在中，
∵，∴设，
∴， ∴
∴，
（2）过点作，垂足为．
易得∽
设，，
∵∥ ∴
∵
∴∽
∴ ∴
即
化简，得
解得 （负值舍去）
∴
（3）过点作，垂足为．
易得∽
设，
∵
∴
∵
∴∽
∴
当和相似时，有两种情况：

∴
即 解得
∴

∴
即 解得
∴
综合、，当和相似时，的长为或．
5.在梯形ABCD中,AD∥BC，.（如图1）
(1)试求的度数；
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.（如图2）
①求证:∽；
②试判断的形状（从边、角两个方面考虑），并加以说明；
③设,试求关于的函数解析式,并写出定义域.
答案：
（1）作，垂足为，
在四边形中，AD∥BC，，
则四边形为正方形
又在中，，
∴.
（2）①∵四边形为正方形，
∴,，
又∵，
∴
又∵,
∴∽.
②是等腰直角三角形，
∵∽，
∴,
又∵,
∴∽，
又在中，,为等腰直角三角形，
∴是等腰直角三角形.
③，（0