数学选择性必修 第二册1.2 瞬时变化率优秀第2课时教案

这是一份数学选择性必修 第二册1.2 瞬时变化率优秀第2课时教案，共7页。教案主要包含了创设情境，引入课题，观察分析，感知概念，抽象概括，形成概念，辨析理解，深化概念，概念应用，巩固内化，归纳总结,反思提升等内容，欢迎下载使用。

课时教学内容
导数是微积分的核心概念之一，是研究函数增减、变化快慢、最值问题的最一般、最有效的工具。教材按照“平均变化率—瞬时变化率—导数的概念—导数的几何意义”的顺序安排，采用“逼近”的方法，从数形结合的角度定义导数，使导数概念的建立形象、直观而又容易理解，突出了导数概念的本质。 平均变化率是导数概念建立的核心，教材通过研究学生熟悉的 “气球膨胀率”、“高台跳水”这两个生活实例，归纳出它们的共同特征，总结出一般函数平均变化率概念，使学生理解平均变化率刻画了函数在某一区间上的变化情况，并掌握平均变化率解法的一般步骤。
从知识形成的先后顺序来看，平均变化率是本章内容学习的核心概念，是研究瞬时变化率及其导数概念的基础，在整个导数学习中占有极其重要的地位。在概念的形成过程中，将进一步渗透从特殊到一般的化归思想，数形结合思想。
课时教学目标
1.利用生活中的实际问题，为了描述运动物体任意时刻的速度，引入瞬时变化率的概念。
2.理解并掌握曲线在某一点处的切线的概念及实际背景;
3.经过本节课的学习，能够理解并运用瞬时变化率解决实际问题，并能理解导数的涵义。
教学重点、难点
1.理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法.
2.用“无限逼近”、“局部以直代曲”的思想理解某一点处切线的斜率.
教学过程设计
ADDIN CNKISM.UserStyle环节一 创设情境，引入课题
问题提出
上面用平均速度刻画了物体在二段时间内运动的快慢.
在实际中,还常常要考虑物体在某一瞬间的速度.比如,我们看到汽车在行驶过程中不断变化的速度表,每个时刻指针指向的数字就是汽车在该时刻的瞬时速度.
如何理解瞬时速度?它与平均速度有何关系呢?
【设计意图】复习平均速度和瞬时速度，对概念进一步抽象，从而得到函数的平均变化率和瞬时变化率的定义.
实例分析
实例1一个小球从高空自由下落,其下落的高度(单位:)与时间(单位:)的函数关系为其中,为重力加速度(取).估算小球在这个时刻的瞬时速度.
分析当时间从变到时,根据平均速度公式
可以求出从到这段时间内小球的平均速度
有时用它来近似表示小球在这个时刻的瞬时速度.
环节二 观察分析，感知概念
为了提高精度,可以缩短时间间隔,如求出到这段时间内的平均速度
用它来近似表示小球在这个时刻的瞬时速度,这样更接近实际情况.
如果时间间隔进一步缩短,那么可以想象,平均速度就更接近小球在这个时刻的瞬时速度.
解将时间间隔每次缩短为上次的,计算出相应的平均速度,得到表2-2.
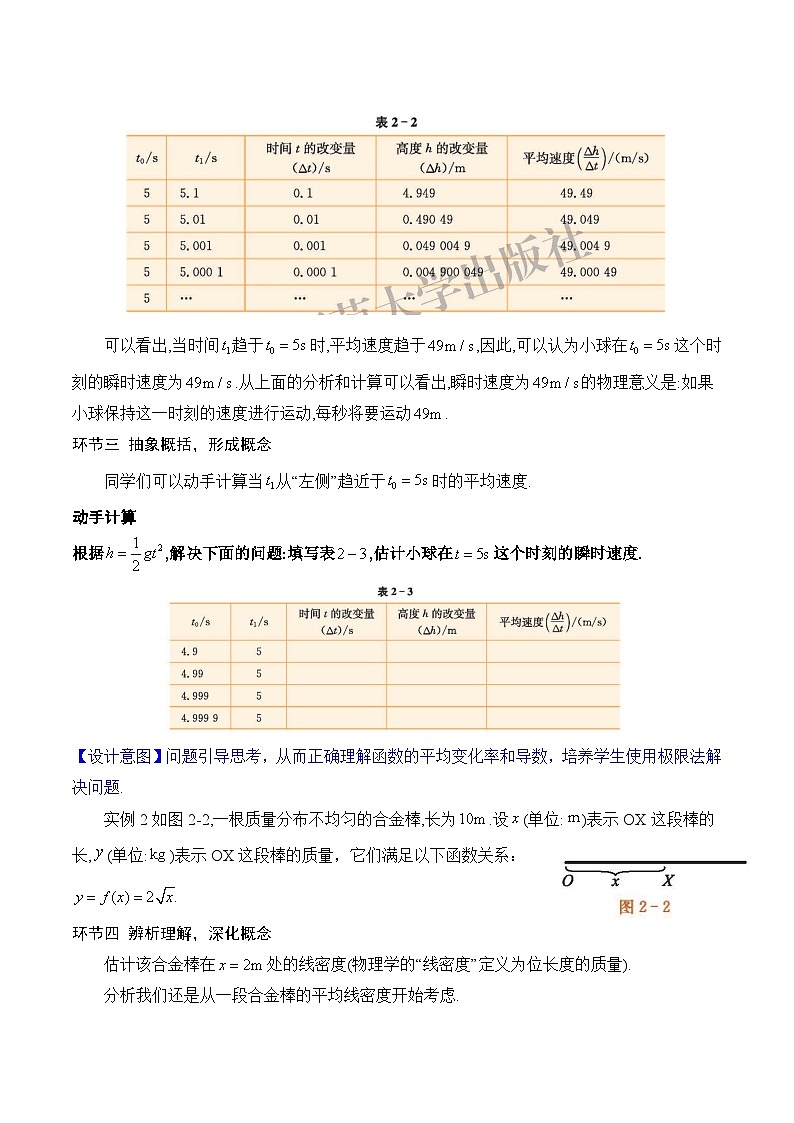
可以看出,当时间趋于时,平均速度趋于,因此,可以认为小球在这个时刻的瞬时速度为.从上面的分析和计算可以看出,瞬时速度为的物理意义是:如果小球保持这一时刻的速度进行运动,每秒将要运动.
环节三 抽象概括，形成概念
同学们可以动手计算当从“左侧”趋近于时的平均速度.
动手计算
根据,解决下面的问题:填写表,估计小球在这个时刻的瞬时速度.
【设计意图】问题引导思考，从而正确理解函数的平均变化率和导数，培养学生使用极限法解决问题.
实例2如图2-2,一根质量分布不均匀的合金棒,长为.设(单位:)表示OX这段棒的长,(单位:)表示OX这段棒的质量，它们满足以下函数关系：
环节四 辨析理解，深化概念
估计该合金棒在处的线密度(物理学的“线密度”定义为位长度的质量).
分析我们还是从一段合金棒的平均线密度开始考虑.
一段合金棒的质量除以这段合金棒的长度,就是这段合金棒的平均线密度.
求出到这段合金棒的平均线密度
它可以近似表示处合金棒的线密度.
与实例1类似,为了提高精度,可以缩短计算线密度所需距离问隔,如取原长度的,即求出到这段合金棒的平均线密度
用它来近似表示合金棒在处的线密度.
环节五 概念应用，巩固内化
如果合金棒的长度进一步缩小,那么可以想象,平均线密度就会更接近合金棒在处的线密度.
解：由,可以计算出相应的平均线密度,得到表2-4.
表2-4
可以看出,当趋于时,平均线密度趋于.
与实例1类似,同学们也可以动手计算当从“左侧”趋近于时的平均线密度,会发现也趋于.
据此,可以认为合金棒在处的线密度约为.
从上面的分析和计算可以看出,线密度为的物理意义是:如果有长的这种线密度的质量均匀的合金棒,其质量将为.
实例1和实例2都是通过减小自变量的改变量(为计算方便选取,也可以选取等),用平均变化率“逼近”瞬时变化率.
【设计意图】例1帮助学生熟悉求导数的具体过程，深化对概念的理解。例2为深化对导数定义式和极限法的理解。
抽象概括
对于一般的函数,在自变量从变到的过程中,
若设,则该函数的平均变化率为
如果当趋于0时,平均变化率趋于某个值,那么这个值就是在点的瞬时变化率.瞬时变化率刻画的是函数在某一点处变化的快慢.
环节六 归纳总结,反思提升
问题1:本节课你学到了什么?
①函数的平均变化率，瞬时变化率的概念;②利用变化率来分析解决实际问题
问题2.如何求瞬时变化率?
一差、二化、三极限
问题3.本节课体现了哪些数学思想方法?
①数形结合的思想方法
②逼近的思想方法
平均变化率是曲线陡峭程度的“数量化”，是一种粗略的刻画
【设计意图】系统梳理整节课所学内容.
环节七目标检测，作业布置
完成教材：教科书习题2.1 A组第1,2,3,4题.
练习
1.在自由落体运动中,根据,仿照实例1,估算当时的瞬时速度.
2.已知函数,求自变量在以下的变化过程中,该函数的平均变化率:
(1)自变量从1变到1.1;
(2)自变量从1变到1.01;
(3)自变量从1变到1.001.
估算当时,该函数的瞬时变化率.
习题2.1
A组
1.下表为3名运动员跑的分段成绩:
(1)这3名运动员谁全程跑得最快?
(2)这3名运动员谁在最后的冲刺阶段跑得最快?
2.已知函数.
(1)当从1变为2时,函数值改变了多少?此时该函数的平均变化率是多少?
(2)当从-1变为1时,函数值改变了多少?此时该函数的平均变化率是多少?
（3）该函数变化的快慢有何特点?求该函数在处的瞬时变化率.
3.某物体走过的路程(单位:)与时间(单位:)的函数关系为,通过平均速度估计物体在下列各时刻的瞬时速度:
(1);
(2);
(3).
4.通过平均变化率估计函数在下列各点处的瞬时变化率:
(1);
(2);
(3).
5.通过平均变化率估计函数在下列各点处的瞬时变化率:
(1);
(2);
(3).
B组
1.有一个长方体的容器(如图),它的宽为,高为.右侧面为一活塞,容器中装有的水.活塞的初始位置(距左侧面)为,水面高度为.当活塞位于距左侧面的位置时,水面高度为.
(1)写出关于的函数解析式;
(2)活塞的位置从变为,水面高度改变了多少?活塞的位置从变为,水面高度改变了多少?以上哪个过程水面高度的变化较快?
(3)试估计当时,水面高度的瞬时变化率.
2.圆的面积随着半径的变化而变化.试分析随半径变化的快慢情况.