






贵州省仁怀市周林学校2023-2024学年八年级下学期期末模拟(达标考试)数学试题(一)
展开一、选择题(以下每小题均有A、B、C、D四个选项,其中只有一项正确,请用2B铅笔在答题卡相应的位置作答. 每小题3分,共36分.)
1.实数-2024的相反数是( )
A.-2024 B.-12024 C.2024 D. 12024
2.教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标不是轴对称图形的是( )
A. B. C. D.
3.甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
第6题图
第3题图
4.将下列各组数据作为三角形的三边长,其中能构成直角三角形的是( )
A.3,4,5 B. 1,2,3 C.6, 7,8 D. 2,3,4
5.下列计算正确的是( )
A.a6÷a2=a3 B.(-a5)2=-a10 C.(a+1)(a-1)=a2-1 D.(a+1)2=a2+1
6.如图,▱ABCD的对角线AC,BD相交于点O,下列结论一定正确的是( )
A. OB=OD B. AB=BC C. AC⊥BD D. ∠ABD=∠CBD
7.下列计算正确的是( )
A. B. C. D.
8.如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连结OE.若AC=6,BD=8,则OE=( )
A.2 B.52
C.3 D.4
9. 如图,以B点为圆心,小于线段BC的长度为半径画弧,分别与ΔABC的AB、BC边交于M点和N点.以N点为圆心,线段MN的长度为半径画弧,两弧交于P点.同理,作出Q点.延长BP、CQ交于D点,从而得到ΔDBC≌ΔABC.其中运用的三角形全等的判定方法是( )
A.SAS
B.ASA
C.AAS
D.SSS
10.某校春季运动会比赛中,八年级(1)班和(2)班的竞技实力相当,关于比赛结果,甲同学说:(1)班与(2)班的得分比为6:5;乙同学说:(1)班得分比(2)班得分的2倍少40分.若设(1)班得x分,(2)班得y分,根据题意所列的方程组为( )
A.5x=6yx=2y+40 B.5x=6yx=2y-40 C.6x=5yx=2y+40 D.6x=5yx=2y-40
11.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的R1),R1的阻值随呼气酒精浓度K的变化而变化(图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A. 呼气酒精浓度K越大,R1的阻值越小 B. 当K=0时,R1的阻值为100Ω
C. 当K=10时,该驾驶员为非酒驾状态 D. 当R1=20时,该驾驶员为醉驾状态
12.在学习过一次函数后,小星准备利用已有知识探索函数y=|x+1|的图象与性质,通过列表、描点、连线,画出了函数的图象,图象与x轴、y轴分别交于A,B两点,则下列说法正确的有( )
①点A的坐标是(1,0); ②函数图象是一个轴对称图形; ③y随着x的增大而增大 ;④该函数有最小值,最小值为0 ; ⑤∠BAO=45 .
A. 1个B. 2个C. 3个D. 4个11题图
二、填空题(每小题4分,共16分.请用黑色墨水笔或黑色签字笔在答题卡相应的位置作答.)
13.因式分解:x2-2x= .
14.已知,一个三角形的三边长的比为3:4:5,且其周长为24,则该三角形的面积为 .
15.已知,在平四边形ABCD中,AB=4,AD=8,对角线AC,BD相交于点O,则AO的取值范围是 .
16.已知,如图,在矩形ABCD中,AD=6,CD=8,在AB上截取AE=AD,连接DE,点H,G分别为AB,AD的中点,点F为DE上的一动点,则△FGH周长的最小值是 .
解答题(本大题共9题,共计98分.在答题卡相应的位置作答.解答应写出必要的文字说明、证明过程或演算步骤.)
17.(本题满分12分)
(2)
18.(本题满分10分)从、、这三个分式中选择两个,添上适当的运算符号进行化简,最后将代入求值.
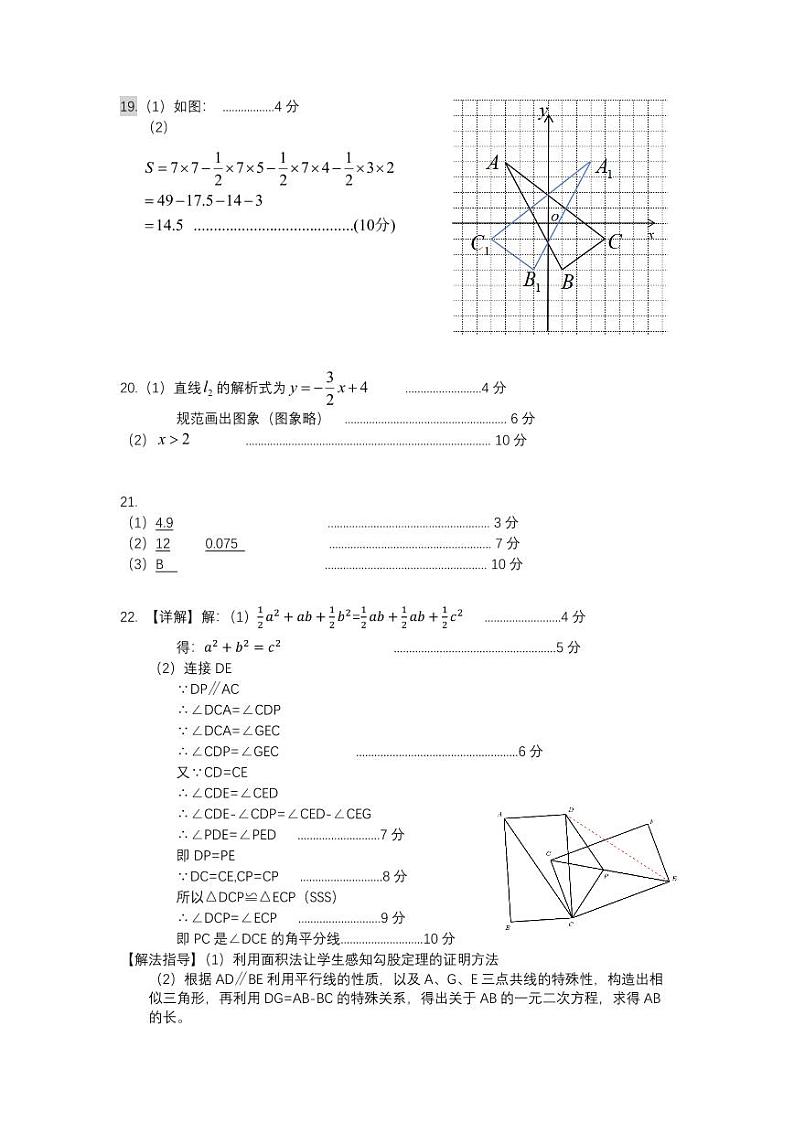
19.(本题满分10分)如图,已知A(-3,4),B(4,-1), C(1,-3).
请在图中做出△ABC关于轴对称的图形
△A1B1C1.
求△A1B1C1的面积.
(本题满分10分)已知直线l1:y=mx+n与直线l2:y=kx+b的交点坐标为,且
直线l2 经过N(-2,7).
在平面直角坐标系中画出直线,并求出直
线的解析式.
结合图像,直接写出不等式mx+n>kx+b的
解集.
(本题满分10分)以下数据是某班学生视力检查结果以及分组统计表.
4.2 4.9 5.0 4.7 4.9 4.3 4.0 4.9 4.8 4.2
4.4 4.6 5.0 4.8 4.1 4.5 4.9 4.1 4.5 4.9
4.2 4.4 4.9 4.5 5.0 4.9 4.3 5.0 4.2 4.3
4.9 4.8 4.5 4.4 4.9 4.8 4.5 4.3 5.0 4.2
(1)该班学生视力的众数为 .
(2)请结合以上数据及表中数据,求= ,= .
(3)该班学生视力的中位数位于 组(填A、B、C、D).
22.(本题满分10分)小方在学习图形的旋转后,开展探究活动:将一个矩形ABCD绕点C顺时针旋转,旋转角为α,得到矩形FGCE.
(图1) (图2)
[探究1]如图1,当α=90°时,B、C、E三点共线,连结AC、CF、AF,小敏在用两种不同方法求梯形ABEF面积时,得出一个结论:AB2+BC2=AC2,意外的证明了勾股定理,下面我们一起来复原小敏的探究过程吧:
(1)请你补全证明过程:
证明:设BC=a,AB=b,AC=c,
方法一:根据梯形的面积公式
S梯形ABEF=12BEAB+EF=12a+ba+b =12a2+ab+12b2
方法二:易证∠ACF=90°,然后把梯形分割成三个部分计算:
S梯形ABEF=SRT△ABC+SRT△CEF+SRT△ACF=12ab+12ab+12c2
即:__________________=________________
整理得____________________
[探究2]如图3,连结AC、EG,过点D作DP∥AC交EG于点P,连接PC.测量发现PC平分∠DCE,小方继续旋转矩形ABCD,发现PC始终平分∠DCE,请你帮小方证明这个结论.
23.(本题满分12分)某酒业销售公司准备出售两种非常具有收藏意义的优质白酒,其中A种白酒680元每瓶(成本为580元/瓶),B种白酒800元每瓶(其成本为650元/瓶),现计划勾调A,B两种白酒共1000瓶作市场调查(A种白酒不得少于300瓶),若A种白酒勾调x瓶,所获利润为y元.
(1)求y与x的函数关系;
(2)求当A种白酒勾调多少瓶时,该公司可获得最大利润,最大利润是多少?
(3)若公司规定,勾调A,B两种白酒必须整百瓶进行勾兑,且售完后的利润不得高于成本的20%,则有多少种勾调方案,哪一种方案能最大限度地让利消费者?
24.(本题满分12分)小灵同学在学习菱形的性质后,进行了深入的探究。如图,在菱形 ABCD中,∠ABC=60,点P(不与点B重合)是对角线BD上一个动点.
(1)【感知应用】如图①,连接AP 、CP,求证:△ABP ≌△CBP ;
(2)【尝试探究】如图②,连接AP,作∠APE =120,交线段BC于点E ,连接AE .求∠PAE 的度数;
(3)【拓展延伸】如图③,连接AP,∠APE =120 ,交线段 BC于点 E ,在点P的运动过程中,探究PB、PD、BE之间的数量关系.
图①
图②
图③
25.(本题满分12分)如图1,在平面直角坐标系中,以O为一顶点的正方形OABC中,点A在x轴上,点C在y轴上,其边长为4.
(1)求直线AC的函数解析式;
(2)如图2,若D为AB的中点,H在OA上,且BH=CD,设直线BH为y1,直线CD为y2,当0
图3
图2
图1
甲
乙
丙
丁
9
8
9
9
1.2
0.4
1.8
0.4
组别
视力范围
频数
频率
A
4.8≤x≤5.0
18
0.45
B
4.5≤x≤4.7
0.175
C
4.2≤x≤4.4
a
D
x≤4.1
3
b
贵州省遵义市仁怀市周林学校2022-2023学年八年级上学期第一次月考数学试题: 这是一份贵州省遵义市仁怀市周林学校2022-2023学年八年级上学期第一次月考数学试题,共2页。
2023-2024学年贵州省仁怀市八年级数学第一学期期末达标测试试题含答案: 这是一份2023-2024学年贵州省仁怀市八年级数学第一学期期末达标测试试题含答案,共7页。试卷主要包含了答题时请按要求用笔,代数式有意义的条件是等内容,欢迎下载使用。
贵州省仁怀市周林学校2022-2023学年八年级上学期半期检测数学试卷(含解析): 这是一份贵州省仁怀市周林学校2022-2023学年八年级上学期半期检测数学试卷(含解析),共19页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。












