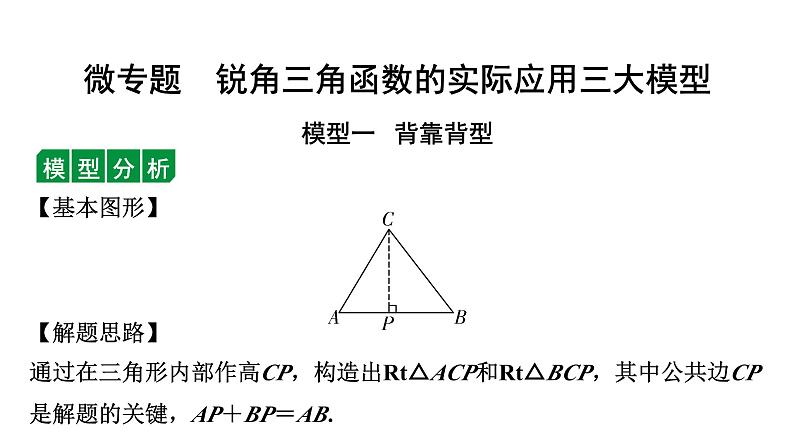
2024徐州中考数学一轮复习之中考考点研究 微专题 锐角三角函数的实际应用三大模型（课件）

这是一份2024徐州中考数学一轮复习之中考考点研究 微专题 锐角三角函数的实际应用三大模型（课件），共17页。PPT课件主要包含了第1题图，第2题图，模型二母子型，第3题图，第4题图，模型三拥抱型，第5题图等内容，欢迎下载使用。

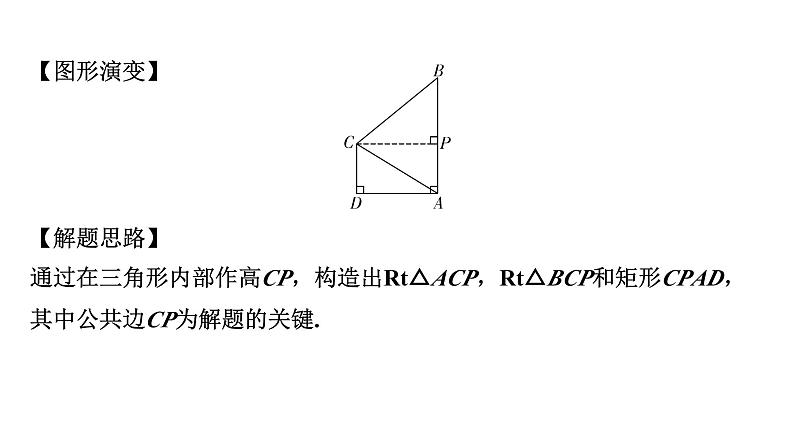
【图形演变】【解题思路】通过在三角形内部作高CP，构造出Rt△ACP，Rt△BCP和矩形CPAD，其中公共边CP为解题的关键.
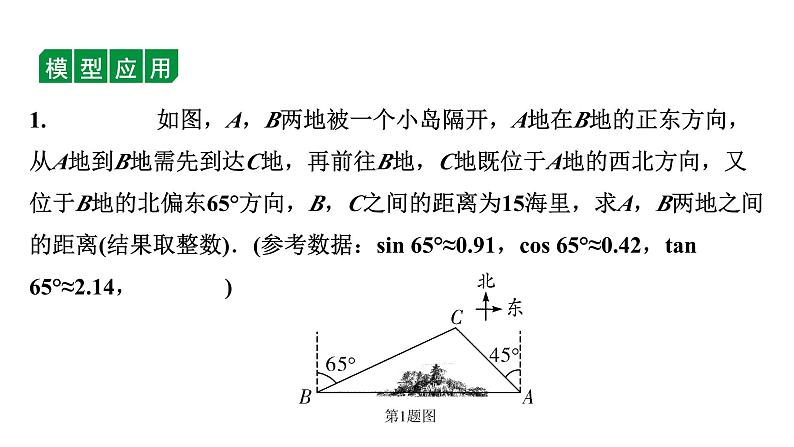
1. 如图，A，B两地被一个小岛隔开，A地在B地的正东方向，从A地到B地需先到达C地，再前往B地，C地既位于A地的西北方向，又位于B地的北偏东65°方向，B，C之间的距离为15海里，求A，B两地之间的距离(结果取整数)．(参考数据：sin 65°≈0.91，cs 65°≈0.42，tan 65°≈2.14， )
解：如图，过点C作CD⊥AB交AB于点D，
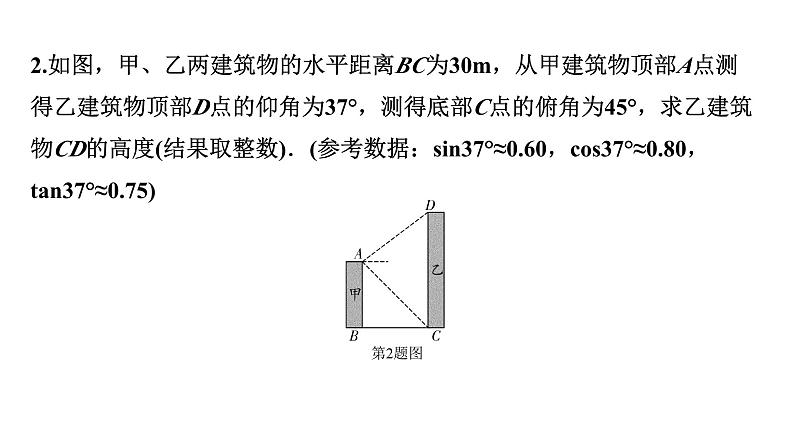
2.如图，甲、乙两建筑物的水平距离BC为30m，从甲建筑物顶部A点测得乙建筑物顶部D点的仰角为37°，测得底部C点的俯角为45°，求乙建筑物CD的高度(结果取整数)．(参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75)
解：如图，过点A作AE⊥CD于点E，则∠DAE＝37°，∠EAC＝45°，
∴CE＝AE·tan∠EAC＝30·tan45°＝30×1＝30m，∴CD＝DE＋CE＝22.5＋30＝52.5≈53m，答：乙建筑物CD的高度约为53m.
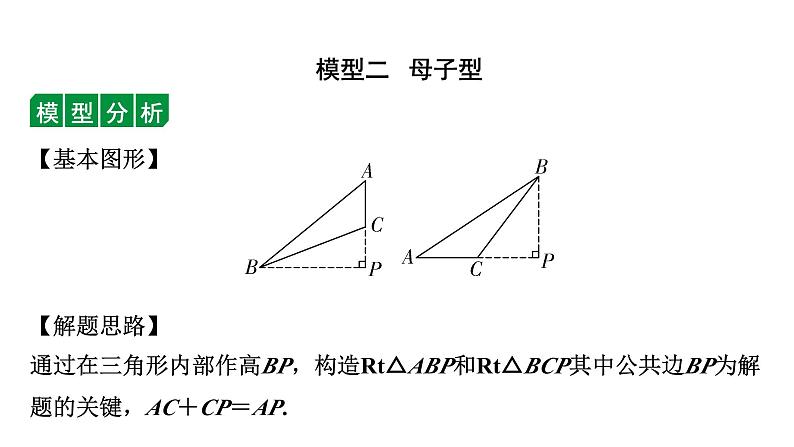
【基本图形】【解题思路】通过在三角形内部作高BP，构造Rt△ABP和Rt△BCP其中公共边BP为解题的关键，AC＋CP＝AP.
【图形演变1】【解题思路】延长DC交AB的延长线于点P，构造出Rt△ACP和Rt△BDP.
【图形演变2】【解题思路】延长AE交CD于点P，构造出Rt△ACP，Rt△CEP和矩形APDB、矩形AEFB、矩形PEFD.
3. 如图，某建筑物AB顶部有一信号塔BC，且点A、B、C在同一条直线上，某同学为了测量建筑物的高度，在地面的D处测得信号塔下端B的仰角为30°，然后他正对塔的方向前进了8米到达地面的E处，又测得信号塔顶端C的仰角为45°，且AC⊥AD，已知信号塔BC的高度为6米，求建筑物AB的高度．(结果取整数，参考数据： )
解：根据题意得DE＝8，BC＝6，∠D＝30°，∠AEC＝45°，设AB＝x，则AC＝x＋6，在Rt△ABD中，AD＝ ,在Rt△AEC中，AE＝AC＝x＋6，∵AD＝AE＋ED，∴ ,解得x≈19米．答：建筑物AB的高度约为19米．
4. 甲、乙两建筑物中间有一花园，小明和小亮想利用所学的知识测量两个建筑物之间的距离，小明先在甲建筑物底部B测得乙建筑物顶部D的仰角为60°，然后回到家中，在家中的阳台E处测得乙建筑物顶部D的仰角为45°，已知点E与点B之间的距离约为36m，A、E、B三点共线，且AB，CD均垂直于BC，求两个建筑物之间的距离BC.(结果保留根号)
解：如图，过点E作EF⊥CD于点F，
【基本图形】【解题思路】△ABC和△DCB均为直角三角形，其中公共边BC为解题的关键.
5. 亮亮同学用所学知识测量小区居民楼AB的高度，如图，她先测得居民楼AB与CD之间的距离AC为35m，然后她站在M点处利用自制的测角仪测得居民楼CD的顶端D点的仰角为45°，居民楼AB的顶端B点的仰角为55°，已知居民楼CD的高度为16.6m，测角仪离地面的高度为1.6m，求居民楼AB的高度(精确到1m)．(参考数据：sin55°≈0.82，cs55°≈0.57，tan55°≈1.43)