2024徐州中考数学二轮重点专题研究 第21课时 锐角三角函数及其应用（课件）

这是一份2024徐州中考数学二轮重点专题研究 第21课时 锐角三角函数及其应用（课件），共28页。PPT课件主要包含了解直角三角形，第1题图，第2题图，类型一背靠背型，第3题图，第4题图，第5题图，类型二母子型，第6题图，第7题图等内容，欢迎下载使用。
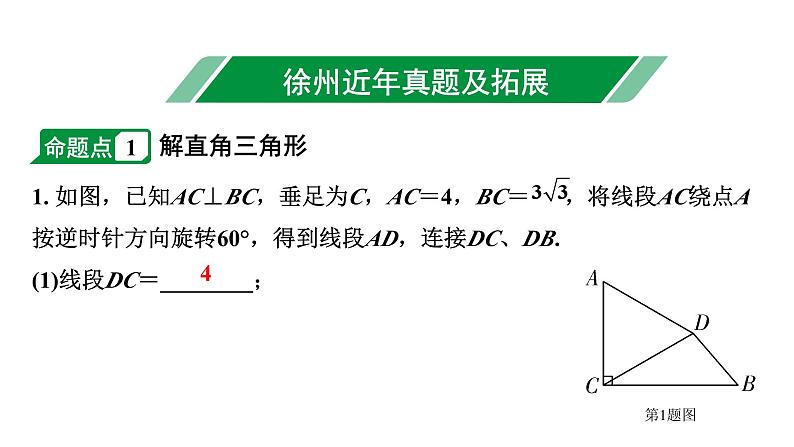
1. 如图，已知AC⊥BC，垂足为C，AC＝4，BC＝ ，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC、DB.(1)线段DC＝________；
(2)求线段DB的长度．
(2)如图，过点D作DE⊥BC于点E.
锐角三角函数的实际应用
2. 如图，无人机于空中A处测得某建筑顶部B处的仰角为45°，测得该建筑底部C处的俯角为17°，若无人机的飞行高度AD为62 m，则该建筑的高度BC为________m．(参考数据：sin17°≈0.29，cs17°≈0.96，tan17°≈0.31)
3. 小红和爸爸绕着小区广场锻炼，如图，在矩形广场ABCD边AB的中点M处有一座雕塑．在某一时刻，小红到达点P时，爸爸到达点Q处，此时雕塑在小红的南偏东45°方向，爸爸在小红的北偏东60°方向，若小红到雕塑的距离PM＝30m，求小红与爸爸的距离PQ.(结果精确到1m，参考数据： )
解：如图，过点P作PN⊥BC于点N.
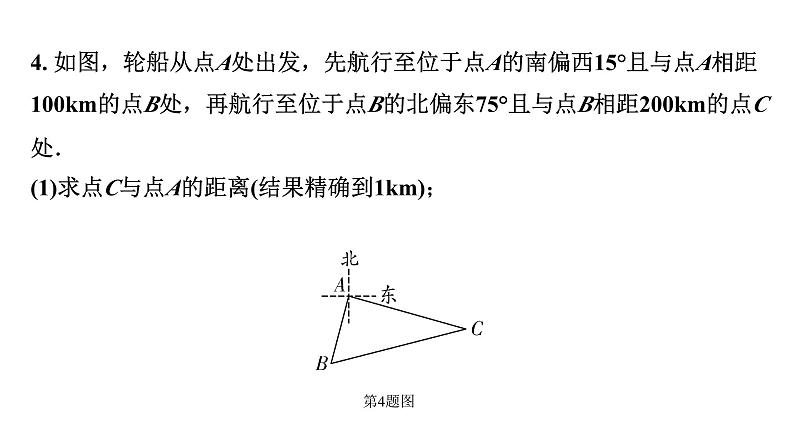
4. 如图，轮船从点A处出发，先航行至位于点A的南偏西15°且与点A相距100km的点B处，再航行至位于点B的北偏东75°且与点B相距200km的点C处．(1)求点C与点A的距离(结果精确到1km)；
解：如解图，过点A作AD⊥BC于点D.
(2)确定点C相对于点A的方向.(参考数据： )
5. 如图，为了测出旗杆AB的高度，在旗杆前的平地上选择一点C，测得旗杆顶部A的仰角为45°，在C、B之间选择一点D(C、D、B三点共线)，测得旗杆顶部A的仰角为75°，且CD＝8m.(1)求点D到CA的距离；
解：(1)如图，过点D作DE⊥AC，垂足为点E.
(2)求旗杆AB的高．(注：结果保留根号)
6. 如图，1号楼在2号楼的南侧，两楼高度均为90m，楼间距为AB.冬至日正午，太阳光线与水平面所成的角为32.3°，1号楼在2号楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为55.7°，1号楼在2号楼墙面上的影高为DA.已知CD＝42m.(1)求楼间距AB；
解：(1)如图，作CM⊥PB于点M，作DN⊥PB于点N，
∴PN≈1.47AB，∵PM＋MN＝PN，(4分)∴0.63AB＋42＝1.47AB，解得AB＝50m.答：楼间距AB约为50m；(5分)
(2)若2号楼共30层，层高均为3m，则点C位于第几层？(参考数据：sin32.3°≈0.53，cs32.3°≈0.85，tan32.3°≈0.63，sin55.7°≈0.83，cs55.7°≈0.56，tan55.7°≈1.47)
(2)∵PM≈0.63AB＝0.63×50＝31.5m，∴(90－31.5)÷3＝19.5(层)．答：点C位于第20层．(8分)
7. 如图，斜坡AB的坡角∠BAC＝13°，计划在该坡面上安装两排平行的光伏板．前排光伏板的一端位于点A，过其另一端D安装支架DE，DE所在的直线垂直于水平线AC，垂足为点F，E为DF与AB的交点，已知AD＝100cm，前排光伏板的坡角∠DAC＝28°.(1)求AE的长(结果取整数)；
解：(1)根据题意可知，∠DFA＝90°，AD＝100，∠DAC＝28°，∴在Rt△DAF中，AF＝AD·cs28°≈100×0.88＝88cm，又∵∠BAC＝13°，∴在Rt△EAF中，AE＝ cm.答：AE的长为91cm；(4分)
(2)冬至日正午，经过点D的太阳光线与AC所成的角∠DGA＝32°.后排光伏板的前端H在AB上．此时，若要后排光伏板的采光不受前排光伏板的影响，则EH的最小值为多少？(结果取整数，参考数据： )
(2)如图，过点A作AQ⊥GD，交GD的延长线于点Q，设DG与AB的交点为N.
又∵∠DAF＝28°，∠EAF＝13°，∴∠QAE＝∠DAF－∠EAF＋∠QAD＝45°，∴AN＝ cm.由(1)可知，AE＝91 cm，∴EN＝AN－AE＝123－91＝32 cm，∵当点H移动到N处时，EH的值最小．答：EH的最小值为32cm(9分)
【对接教材】苏科：九下第7章P94－P121
锐角三角函数的定义：如图①，在Rt△ABC中，∠ACB＝90°，∠A为△ABC中的一锐角， ________ 则有： ________ ________
直角三角形的边角关系(如图①)
三边关系：a2＋________＝c2三角关系：∠A＋________＝∠C＝90°边、角间关系：sinA＝csB＝ ，csA＝________＝ ，tanA＝________，tanB＝________
锐角三角函数的实际应用
1. 仰角、俯角：如图②，在视线与水平线所成的锐角中，视线在水平线上方的角叫________，视线在水平线下方的角叫________2. 方向角：一般指以观测者的位置为中心，将正北或正南方向作为始方向旋转到目标方向线所成的角(一般指锐角)，通常表达成北(南)偏东(西)多少度，如图③，A点位于O点的北偏东30°方向，B点位于O点的南偏东60°方向，C点位于O点的北偏西45°方向(或西北方向)3. 坡度(坡比)、坡角：如图④，坡面的铅直高度h和水平宽度l的比叫坡度(坡比)，用字母i表示；坡面与水平线的夹角α叫坡角，i＝tanα＝________