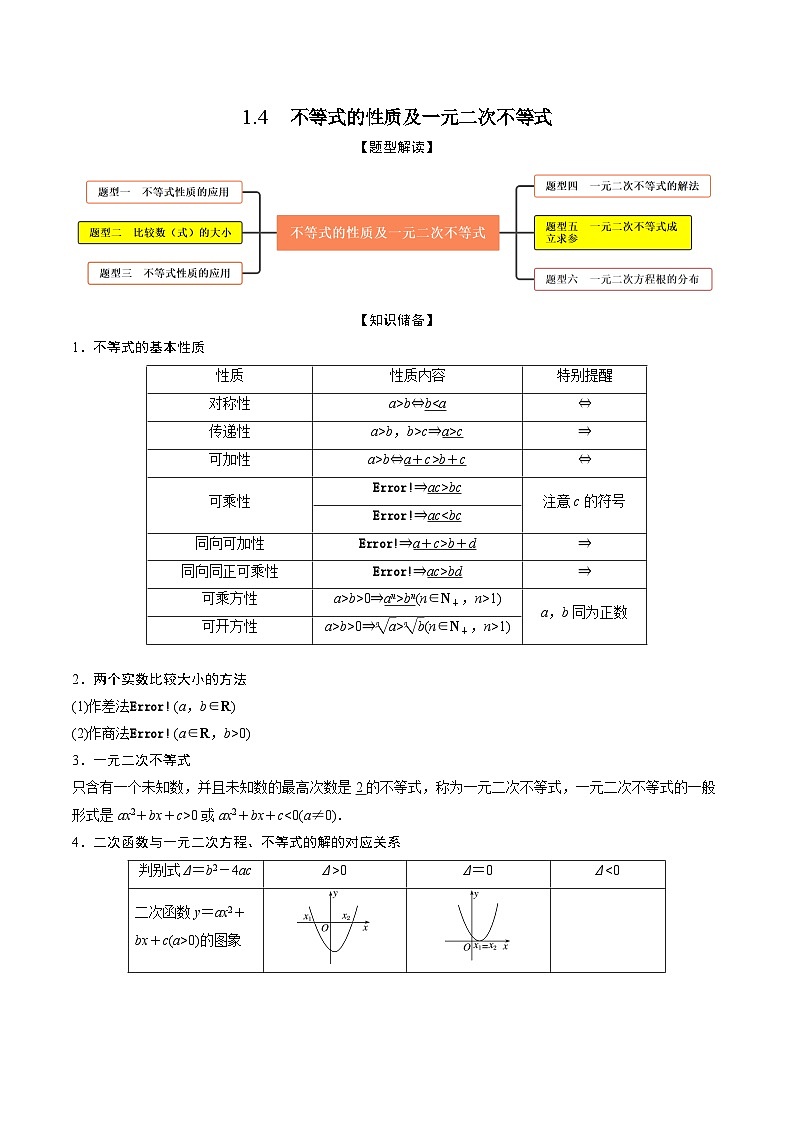
高考数学大一轮复习精讲精练(新高考地区)1.4不等式的性质及一元二次不等式(精讲)(原卷版+解析)

展开

这是一份高考数学大一轮复习精讲精练(新高考地区)1.4不等式的性质及一元二次不等式(精讲)(原卷版+解析)，共28页。

【知识储备】
1．不等式的基本性质
2．两个实数比较大小的方法
(1)作差法eq \b\lc\{\rc\ (\a\vs4\al\c1(a－b>0⇔a>b,a－b＝0⇔a＝b,a－b<0⇔a(2)作商法eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(a,b)>1⇔a>b,\f(a,b)＝1⇔a＝b,\f(a,b)<1⇔a0)
3．一元二次不等式
只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式，一元二次不等式的一般形式是ax2＋bx＋c>0或ax2＋bx＋c<0(a≠0)．
4．二次函数与一元二次方程、不等式的解的对应关系
5.分式不等式与整式不等式
(1)eq \f(fx,gx)>0(<0)⇔f(x)g(x)>0(<0)；
(2)eq \f(fx,gx)≥0(≤0)⇔f(x)g(x)≥0(≤0)且g(x)≠0.
【题型精讲】
【题型一不等式性质的应用】
必备技巧判断不等式的常用方法
(1)直接利用不等式的性质逐个验证，利用不等式的性质判断不等式是否成立时要特别注意前提条件．
(2)利用特殊值法排除错误答案．
(3)利用函数的单调性，当直接利用不等式的性质不能比较大小时，可以利用指数函数、对数函数、幂函数等函数的单调性来比较．
例1 (2023·辽宁·东北育才学校一模）若a，b，c∈R，a>b，则下列不等式恒成立的是（）
A．b2
C．>D．a|c|>b|c|
例2 (2023·浙江模拟）已知，是正实数，则下列式子中能使恒成立的是（）
A．B．C．D．
【题型精练】
1. (2023·北京海淀·二模）已知，且，则（）
A．B．
C．D．
2．（多选题）(2023·福建三明·模拟预测）设，且，则（）
A．B．C．D．
【题型二比较数（式）的大小】
必备技巧比较大小的常用方法
(1)作差法：①作差；②变形；③定号；④得出结论．
(2)作商法：①作商；②变形；③判断商与1的大小关系；④得出结论．
(3)构造函数，利用函数的单调性比较大小．
例3 (2023·江苏·高三专题复习）设x，y为正数，比较与的大小.
例4 (2023·湖南·高三课时练习）比较与的大小．
例5 (2023·全国·高三专题练习）已知，，，则，，的大小关系为（）
A．B．
C．D．
【题型精练】
1．(2023·重庆·模拟预测）若，则（）
A．B．
C．D．
2. (2023·广东茂名·高三阶段练习）（多选）已知，，（其中为自然对数的底数），则，，的大小关系为（）
A．B．C．D．
3. (2023·重庆市育才中学模拟预测）（多选）若a＞b＞0＞c，则( )
A．B．C．D．
【题型三不等式性质的应用】
必备技巧不等式性质的应用
求代数式的取值范围，一般是利用整体思想，通过“一次性”不等关系的运算求得整体范围．
例6 （多选）(2023·山东·模拟预测）已知实数x，y满足则（）
A．的取值范围为B．的取值范围为
C．的取值范围为D．的取值范围为
例7 (2023·江西·二模）已知，，则6x＋5y的取值范围为______．
【题型精练】
1．（2023·东北三省四市联考）已知角α，β满足－eq \f(π,2)<α－β2. (2023·全国·高三专题练习（文））已知－3A．(1，3) B． C． D．
【题型四一元二次不等式的解法】
必备技巧含参的不等式解法
(1)根据二次项系数为正、负及零进行分类．
(2)根据判别式Δ与0的关系判断根的个数．
(3)有两个根时，有时还需根据两根的大小进行讨论．
例8 (2023·河北·模拟预测）已知集合，，则（）
A．B．C．D．
例9 (2023·河北唐山·高三月考）已知关于x的不等式：．
(1)当时，解此不等式；
(2)当时，解此不等式．
【题型精练】
1．(2023·全国·高三专题练习）已知函数（且）的图象过定点，则不等式的解集为（）
A．B．C．D．
2. (2023·福建省长汀县第一中学高三阶段练习）解关于的不等式：.
【题型五一元二次不等式成立求参】
必备技巧一元二次不等式求参
(1)解决恒成立问题一定要搞清谁是自变量，谁是参数，一般地，知道谁的范围，谁就是变量，求谁的范围，谁就是参数．
(2)对于二次不等式恒成立问题常见的类型有两种，一是在全集R上恒成立，二是在某给定区间上恒成立．
对第一种情况恒大于0就是相应的二次函数的图象全部在x轴上方，恒小于0就是相应的二次函数的图象全部在x轴下方；
对第二种情况，要充分结合函数图象进行分类讨论(也可采用分离参数的方法)．
例10 (2023·全国·高三专题练习）已知，“对恒成立”的一个充要条件是（）
A．B．C．D．
例11 (2023·宁夏·隆德县中学高三阶段练习）已知命题“，”是真命题，则实数的取值范围（）
A．B． C．）D．
例12 (2023·全国·高三专题练习）若对任意的恒成立，则m的取值范围是（）
A．B．C．D．
例13 (2023·全国·高三专题练习）已知，，不等式恒成立，则的取值范围为
A．，，B．，，
C．，，D．
【题型精练】
1．(2023·江苏南通·模拟预测）当时，不等式恒成立，则实数的取值范围是（）
A．B．
C．D．
2. (2023·全国·高三专题练习）不等式对一切恒成立，则实数的取值范围是（）
A．B．
C． D．
3. (2023·全国·高三专题练习）不等式对一切恒成立，则实数的取值范围是（）
A．B．
C． D．
4. (2023·天津·耀华中学高三期中）若命题“，使得不等式”成立，则实数的取值集合是（）
A．B．
C．D．
【题型六一元二次方程根的分布】
必备技巧一元二次方程根的分布情况
表一：(两根与0的大小比较即根的正负情况)
表二：(两根与k的大小比较)
表三：(根在区间上的分布)
根在区间上的分布还有一种情况：两根分别在区间(m，n)外，即在区间两侧x1n，(图形分别如下)需满足的条件是
(1)a>0时，eq \b\lc\{\rc\ (\a\vs4\al\c1(fm<0，,fn<0；))
(2)a<0时，eq \b\lc\{\rc\ (\a\vs4\al\c1(fm>0，,fn>0.))
对以上的根的分布表中，两根有且仅有一根在(m，n)内有以下特殊情况：
(ⅰ)若f(m)＝0或f(n)＝0，则此时f(m)·f(n)<0不成立，但对于这种情况是知道了方程有一根为m或n，可以求出另外一根，然后可以根据另一根在区间(m，n)内，从而可以求出参数的值．如方程mx2－(m＋2)x＋2＝0在区间(1,3)上有一根，因为f(1)＝0，所以mx2－(m＋2)x＋2＝(x－1)(mx－2)，另一根为eq \f(2,m)，由1(ⅱ)方程有两个相等的根，且这个根在区间(m，n)内，即Δ＝0，此时由Δ＝0可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数．
例14 (2023·全国·专题练习）已知方程有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是（）
A．B．
C．D．
例15 (2023·浙江·高三专题练习）若关于的方程有两个不同的正根，则实数的取值范围是（）
A．B．C．D．
例16 (2023·全国·高三专题练习）若不等式在上有解，则实数的取值范围是（）
A．B．
C．D．
【题型精练】
1．（2023·江苏模拟）设a为实数，若方程在区间上有两个不相等的实数解，则a的取值范围是（）.
A．B．
C．D．
2. (2023·黑龙江·哈尔滨市第六中学校高三开学考试）关于的方程的两根都大于2，则的取值范围是（）
A．B．
C．D．
3.(2023·全国·单元测试）为何值时，关于的方程的两根：
为正数根；
为异号根且负根绝对值大于正根；
都大于1；
一根大于2，一根小于2；
（5）两根在0，2之间.
性质
性质内容
特别提醒
对称性
a>b⇔b⇔
传递性
a>b，b>c⇒a>c
⇒
可加性
a>b⇔a＋c>b＋c
⇔
可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c>0))⇒ac>bc
注意c的符号
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c<0))⇒ac同向可加性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c>d))⇒a＋c>b＋d
⇒
同向同正可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b>0,c>d>0))⇒ac>bd
⇒
可乘方性
a>b>0⇒an>bn(n∈N＋，n>1)
a，b同为正数
可开方性
a>b>0⇒eq \r(n,a)>eq \r(n,b)(n∈N＋，n>1)
判别式Δ＝b2－4ac
Δ>0
Δ＝0
Δ<0
二次函数y＝ax2＋bx＋c(a>0)的图象
方程ax2＋bx＋c＝0
(a>0)的根
有两个不相等的实数根x1，x2(x1有两个相等的实数根
x1＝x2＝－eq \f(b,2a)
没有实数根
ax2＋bx＋c>0(a>0)的解集
{x|xx2}
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠－\f(b,2a)))))
R
ax2＋bx＋c<0(a>0)的解集
{x|x1< x∅
∅
分布情况
两个负根即两根都小于0(x1<0，x2<0)
两个正根即两根都大于0(x1>0，x2>0)
一正根一负根即一个根小于0，一个根大于0(x1<0大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,f0>0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,f0>0))
f(0)<0
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,f0<0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,f0<0))
f(0)>0
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,a·f0>0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,a·f0>0))
a·f(0)<0
分布情况
两根都小于k即x1两根都大于k即x1>k，x2>k
一个根小于k，一个根大于k即x1大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,fk>0))
f(k)<0
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,fk<0))
f(k)>0
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,a·fk>0))
a·f(k)<0
分布情况
两根都在(m，n)内
两根有且仅有一根在(m，n)内(图象有两种情况，只画了一种)
一根在(m，n)内，另一根在(p，q)内，mp大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm>0，,fn>0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fm>0，,fn<0，,fp<0，,fq>0))或
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm<0，,fn<0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fm<0，,fn>0，,fp>0，,fq<0))或
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm·fn>0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))
1.4 不等式的性质及一元二次不等式
【题型解读】
【知识储备】
1．不等式的基本性质
2．两个实数比较大小的方法
(1)作差法eq \b\lc\{\rc\ (\a\vs4\al\c1(a－b>0⇔a>b,a－b＝0⇔a＝b,a－b<0⇔a(2)作商法eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(a,b)>1⇔a>b,\f(a,b)＝1⇔a＝b,\f(a,b)<1⇔a0)
3．一元二次不等式
只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式，一元二次不等式的一般形式是ax2＋bx＋c>0或ax2＋bx＋c<0(a≠0)．
4．二次函数与一元二次方程、不等式的解的对应关系
5.分式不等式与整式不等式
(1)eq \f(fx,gx)>0(<0)⇔f(x)g(x)>0(<0)；
(2)eq \f(fx,gx)≥0(≤0)⇔f(x)g(x)≥0(≤0)且g(x)≠0.
【题型精讲】
【题型一不等式性质的应用】
必备技巧判断不等式的常用方法
(1)直接利用不等式的性质逐个验证，利用不等式的性质判断不等式是否成立时要特别注意前提条件．
(2)利用特殊值法排除错误答案．
(3)利用函数的单调性，当直接利用不等式的性质不能比较大小时，可以利用指数函数、对数函数、幂函数等函数的单调性来比较．
例1 (2023·辽宁·东北育才学校一模）若a，b，c∈R，a>b，则下列不等式恒成立的是（）
A．b2
C．>D．a|c|>b|c|
答案：C
【解析】当a=1，b=-2时，满足a>b，但，a2因>0，a>b，由不等式性质得，C正确；
当c=0时，a|c|>b|c|不成立，排除D，
故选：C
例2 (2023·浙江模拟）已知，是正实数，则下列式子中能使恒成立的是（）
A．B．C．D．
答案：B
【解析】对于A，取，该不等式成立，但不满足；
对于C，该不等式等价于，取，，该不等式成立，但不满足；
对于D，该不等式等价于，取，，该不等式成立，但不满足；
下面证明B
法一：不等式等价于，而.函数在上单增，故.
法二：若，则，故，矛盾.故选：B
【题型精练】
1. (2023·北京海淀·二模）已知，且，则（）
A．B．
C．D．
答案：B
【解析】对于A，令，显然，错误；
对于B，，
又不能同时成立，故，正确；
对于C，取，则，错误；
对于D，取，则，错误.
故选：B.
2．（多选题）(2023·福建三明·模拟预测）设，且，则（）
A．B．C．D．
答案：BC
【解析】因为，，所以，的符号不能确定，
当时，，故A错误，
因为，，所以，故B正确，
因为，所以，故C正确，
因为，所以，所以，所以，故D错误，
故选：BC
【题型二比较数（式）的大小】
必备技巧比较大小的常用方法
(1)作差法：①作差；②变形；③定号；④得出结论．
(2)作商法：①作商；②变形；③判断商与1的大小关系；④得出结论．
(3)构造函数，利用函数的单调性比较大小．
例3 (2023·江苏·高三专题复习）设x，y为正数，比较与的大小.
【解】因为为整数，则且，
由，当且仅当时，等号成立，
所以，所以.
例4 (2023·湖南·高三课时练习）比较与的大小．
【解析】,
<.
例5 (2023·全国·高三专题练习）已知，，，则，，的大小关系为（）
A．B．
C．D．
答案：C
【解析】∵，构造函数，，
令，则，∴在上单减，∴，
故，所以在上单减，
∴，
同理可得，故，故选：C.
【题型精练】
1．(2023·重庆·模拟预测）若，则（）
A．B．
C．D．
答案：A
【解析】∵，，∴
又，∴∴
，又∴
综上：故选：A
2. (2023·广东茂名·高三阶段练习）（多选）已知，，（其中为自然对数的底数），则，，的大小关系为（）
A．B．C．D．
答案：AD
【解析】令，，则，所以当时，当时，所以在上单调递减，在上单调递增，所以，所以，，又，所以，所以；故选：AD
3. (2023·重庆市育才中学模拟预测）（多选）若a＞b＞0＞c，则( )
A．B．C．D．
答案：ABD
【解析】
A：，∵，，
，，故A正确；
B：，∵，∴，
，故B正确；
C：时，在单调递减，∵，故C错误；
D：∵a＞b＞0＞c，∴－c＞0，∴，∵a≠b，故等号取不到，故，故D正确.
故选：ABD.
【题型三不等式性质的应用】
必备技巧不等式性质的应用
求代数式的取值范围，一般是利用整体思想，通过“一次性”不等关系的运算求得整体范围．
例6 （多选）(2023·山东·模拟预测）已知实数x，y满足则（）
A．的取值范围为B．的取值范围为
C．的取值范围为D．的取值范围为
答案：ABD
【解析】因为，所以.因为，所以，则，故A正确；
因为，所以.因为，所以，所以，所以，故B正确；
因为，所以，则，故C错误；
因为，所以，则，故D正确.
故选：ABD.
例7 (2023·江西·二模）已知，，则6x＋5y的取值范围为______．
答案：
【解析】，即
故6x＋5y的取值范围为．
故答案为：
【题型精练】
1．（2023·东北三省四市联考）已知角α，β满足－eq \f(π,2)<α－β【解析】结合题意可知，3α－β＝2(α－β)＋(α＋β)，且2(α－β)∈(－π，π)，(α＋β)∈(0，π)，
由不等式的性质可知3α－β的取值范围是(－π，2π)
2. (2023·全国·高三专题练习（文））已知－3A．(1，3) B． C． D．
答案：A
【解析】因为－3【题型四一元二次不等式的解法】
必备技巧含参的不等式解法
(1)根据二次项系数为正、负及零进行分类．
(2)根据判别式Δ与0的关系判断根的个数．
(3)有两个根时，有时还需根据两根的大小进行讨论．
例8 (2023·河北·模拟预测）已知集合，，则（）
A．B．C．D．
答案：B
【解析】解不等式，，
解不等式得，，
；
故选：B.
例9 (2023·河北唐山·高三月考）已知关于x的不等式：．
(1)当时，解此不等式；
(2)当时，解此不等式．
答案：(1)或
(2)当时，解集为；当时，解集为；当时，解集为
【解析】(1)当a＝－2时，不等式－2x2＋5x＋3＜0
整理得(2x＋1)(x－3)＞0，解得x＜－或x＞3，
当a＝－2时，原不等式解集为{x|x＜－或x＞3}．
(2)当a＞0时，不等式ax2－(3a＋1)x＋3＜0
整理得：(x－3)(x－)＜0，
当a＝时，＝3，此时不等式无解；
当0＜a＜时，＞3，解得3＜x＜；
当a＞时，＜3，解得＜x＜3；
综上：当a＝时，解集为；
当0＜a＜时，解集为{x|3＜x＜}；
当a＞时，解集为{x|＜x＜3}.
【题型精练】
1．(2023·全国·高三专题练习）已知函数（且）的图象过定点，则不等式的解集为（）
A．B．C．D．
答案：D
【解析】当时，，故，所以不等式为，解得，所以不等式的解集为.
故选：D
2. (2023·福建省长汀县第一中学高三阶段练习）解关于的不等式：.
【解析】当a＋1=0即 a＝-1时，原不等式变为－x＋2<0，即x>2.
当a>-1时，原不等式可转化为，
∴方程的根为.
若-12，解得2若a＝，则＝2，解得x∈∅；
若a>，则<2，解得综上，
当a>时，原不等式的解集为{x|当a＝时，原不等式的解集为∅；
当-1当a＝-1时，原不等式的解集为{x|x>2}.
【题型五一元二次不等式成立求参】
必备技巧一元二次不等式求参
(1)解决恒成立问题一定要搞清谁是自变量，谁是参数，一般地，知道谁的范围，谁就是变量，求谁的范围，谁就是参数．
(2)对于二次不等式恒成立问题常见的类型有两种，一是在全集R上恒成立，二是在某给定区间上恒成立．
对第一种情况恒大于0就是相应的二次函数的图象全部在x轴上方，恒小于0就是相应的二次函数的图象全部在x轴下方；
对第二种情况，要充分结合函数图象进行分类讨论(也可采用分离参数的方法)．
例10 (2023·全国·高三专题练习）已知，“对恒成立”的一个充要条件是（）
A．B．C．D．
答案：B
【解析】当时，，对恒成立；
当时，若，对恒成立，
则必须有，解之得，
综上，的取值范围为.
故“对恒成立”的一个充要条件是，
故选：B
例11 (2023·宁夏·隆德县中学高三阶段练习）已知命题“，”是真命题，则实数的取值范围（）
A．B． C．）D．
答案：D
【解析】由题意，命题“，”是真命题
故，解得或.
则实数的取值范围是
故选：D.
例12 (2023·全国·高三专题练习）若对任意的恒成立，则m的取值范围是（）
A．B．C．D．
答案：A
【解析】因为对任意的恒成立，
所以对任意的恒成立，
因为当，，
所以，，
即m的取值范围是
故选：A
例13 (2023·全国·高三专题练习）已知，，不等式恒成立，则的取值范围为
A．，，B．，，
C．，，D．
答案：C
【解析】令，
则不等式恒成立转化为在上恒成立．
有，即，
整理得：，
解得：或．
的取值范围为．
故选：C．
【题型精练】
1．(2023·江苏南通·模拟预测）当时，不等式恒成立，则实数的取值范围是（）
A．B．
C．D．
答案：A
【解析】由题意，当时，不等式恒成立，故
解得，故实数的取值范围是
故选：A
2. (2023·全国·高三专题练习）不等式对一切恒成立，则实数的取值范围是（）
A．B．
C． D．
答案：A
【解析】令，对一切均大于0恒成立，
所以，或，
或，
解得或，，或，
综上，实数的取值范围是，或.
故选：A.
3. (2023·全国·高三专题练习）不等式对一切恒成立，则实数的取值范围是（）
A．B．
C． D．
答案：A
【解析】令，对一切均大于0恒成立，
所以，或，
或，
解得或，，或，
综上，实数的取值范围是，或.
故选：A.
4. (2023·天津·耀华中学高三期中）若命题“，使得不等式”成立，则实数的取值集合是（）
A．B．
C．D．
答案：B
【解析】命题“，使得不等式”成立，
当时，不等式为，显然有解，成立；
当时，开口向下，必然，使得不等式成立，；
当，即，解得或，所以或．
综上可得或．
故选：．
【题型六一元二次方程根的分布】
必备技巧一元二次方程根的分布情况
表一：(两根与0的大小比较即根的正负情况)
表二：(两根与k的大小比较)
表三：(根在区间上的分布)
根在区间上的分布还有一种情况：两根分别在区间(m，n)外，即在区间两侧x1n，(图形分别如下)需满足的条件是
(1)a>0时，eq \b\lc\{\rc\ (\a\vs4\al\c1(fm<0，,fn<0；))
(2)a<0时，eq \b\lc\{\rc\ (\a\vs4\al\c1(fm>0，,fn>0.))
对以上的根的分布表中，两根有且仅有一根在(m，n)内有以下特殊情况：
(ⅰ)若f(m)＝0或f(n)＝0，则此时f(m)·f(n)<0不成立，但对于这种情况是知道了方程有一根为m或n，可以求出另外一根，然后可以根据另一根在区间(m，n)内，从而可以求出参数的值．如方程mx2－(m＋2)x＋2＝0在区间(1,3)上有一根，因为f(1)＝0，所以mx2－(m＋2)x＋2＝(x－1)(mx－2)，另一根为eq \f(2,m)，由1(ⅱ)方程有两个相等的根，且这个根在区间(m，n)内，即Δ＝0，此时由Δ＝0可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数．
例14 (2023·全国·专题练习）已知方程有两个不相等的实数根，且两个实数根都大于2，则实数m的取值范围是（）
A．B．
C．D．
答案：C
【解析】令
由题可知：
则，即故选：C
例15 (2023·浙江·高三专题练习）若关于的方程有两个不同的正根，则实数的取值范围是（）
A．B．C．D．
答案：C
【解析】因为关于的方程有两个不同的正根，
所以，解得，故实数的取值范围是.
故选：C
例16 (2023·全国·高三专题练习）若不等式在上有解，则实数的取值范围是（）
A．B．
C．D．
答案：B
【解析】因为不等式在上有解，
所以不等式在上有解，令，则，
所以，所以实数的取值范围是
故选：B
【题型精练】
1．（2023·江苏模拟）设a为实数，若方程在区间上有两个不相等的实数解，则a的取值范围是（）.
A．B．
C．D．
答案：C
【解析】令，由方程在区间上有两个不相等的实数解可得
，即或，解得，故选：C
2. (2023·黑龙江·哈尔滨市第六中学校高三开学考试）关于的方程的两根都大于2，则的取值范围是（）
A．B．
C．D．
答案：B
【解析】解：∵关于的方程的两根都大于2，
令，可得，即，
求得，
故选：B.
3.(2023·全国·单元测试）为何值时，关于的方程的两根：
为正数根；
为异号根且负根绝对值大于正根；
都大于1；
一根大于2，一根小于2；
（5）两根在0，2之间.
答案：（1）或；（2）；（3）；（4）；（5）或
【解析】设函数由题意可得，方程有两根设为，对称轴，解得或
（1）由题意可得或
（2）由题意可得
（3）由题意可得
（4）由题意可得
（5）由题意可得或
性质
性质内容
特别提醒
对称性
a>b⇔b⇔
传递性
a>b，b>c⇒a>c
⇒
可加性
a>b⇔a＋c>b＋c
⇔
可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c>0))⇒ac>bc
注意c的符号
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c<0))⇒ac同向可加性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b,c>d))⇒a＋c>b＋d
⇒
同向同正可乘性
eq \b\lc\ \rc\}(\a\vs4\al\c1(a>b>0,c>d>0))⇒ac>bd
⇒
可乘方性
a>b>0⇒an>bn(n∈N＋，n>1)
a，b同为正数
可开方性
a>b>0⇒eq \r(n,a)>eq \r(n,b)(n∈N＋，n>1)
判别式Δ＝b2－4ac
Δ>0
Δ＝0
Δ<0
二次函数y＝ax2＋bx＋c(a>0)的图象
方程ax2＋bx＋c＝0
(a>0)的根
有两个不相等的实数根x1，x2(x1有两个相等的实数根
x1＝x2＝－eq \f(b,2a)
没有实数根
ax2＋bx＋c>0(a>0)的解集
{x|xx2}
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠－\f(b,2a)))))
R
ax2＋bx＋c<0(a>0)的解集
{x|x1< x∅
∅
分布情况
两个负根即两根都小于0(x1<0，x2<0)
两个正根即两根都大于0(x1>0，x2>0)
一正根一负根即一个根小于0，一个根大于0(x1<0大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,f0>0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,f0>0))
f(0)<0
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,f0<0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,f0<0))
f(0)>0
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)<0，,a·f0>0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>0，,a·f0>0))
a·f(0)<0
分布情况
两根都小于k即x1两根都大于k即x1>k，x2>k
一个根小于k，一个根大于k即x1大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,fk>0))
f(k)<0
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,fk<0))
f(k)>0
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)0))
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,－\f(b,2a)>k，,a·fk>0))
a·f(k)<0
分布情况
两根都在(m，n)内
两根有且仅有一根在(m，n)内(图象有两种情况，只画了一种)
一根在(m，n)内，另一根在(p，q)内，mp大致图象(a>0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm>0，,fn>0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fm>0，,fn<0，,fp<0，,fq>0))或
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))
大致图象(a<0)
得出的结论
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm<0，,fn<0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fm<0，,fn>0，,fp>0，,fq<0))或
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))
综合结论
(不讨论a)
eq \b\lc\{\rc\ (\a\vs4\al\c1(Δ>0，,fm·fn>0，,m<－\f(b,2a)f(m)·f(n) <0
eq \b\lc\{\rc\ (\a\vs4\al\c1(fmfn<0，,fpfq<0))