
高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02讲平面向量的加、减法运算(原卷版+解析)
展开向量的加法运算
知识点2 向量的减法
1、相反向量
(1)我们规定,与向量a长度相等,方向相反的向量,叫做a的相反向量,记作-a.
(2)-(-a)=a,a+(-a)=(-a)+a=0.若,互为相反向量,则,,0
(3)零向量的相反向量仍是零向量,即0=-0.
2、向量的减法运算
考点一 向量的加法运算
解题方略
(1)平行四边形法则的应用前提:两个向量是从同一点出发的不共线向量.
三角形法则应用的前提:两个向量“首尾相接”.
当两个向量不共线时,三角形法则和平行四边形法则实质是一样的.三角形法则作出的图形是平行四边形法则作出图形的一半.但当两个向量共线时,平行四边形法则便不再适用.
向量的加法法则
已知向量a与向量b,要作出和向量a+b,关键是准确规范地依据向量的三角形法则和平行四边形法则作图.
【例1】如图,已知向量,,求作向量.
变式1:如图,在下列各小题中,已知向量、,分别用两种方法求作向量.
向量的加法运算
在向量的加法运算中,通过向量加法的交换律,使各向量“首尾相连”,通过加法的结合律调整向量相加的顺序,可以省去画图步骤,加快解题速度.
【例2】化简:(1)eq \(BC,\s\up6(→))+eq \(AB,\s\up6(→)); (2)eq \(DB,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→)); (3)eq \(AB,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(FA,\s\up6(→)).
变式1:向量﹒化简后等于( )
A.B.0C.D.
变式2:化简下列各式:①;②;③;④.其中结果为的个数是( )
A.1B.2C.3D.4
变式3:已知、是不平行的向量,若,,,则下列关系中正确的是( )
A. B. C. D.
【例3】已知正六边形,则 ( )
A.B.C.D.
变式1:如图,在平行四边形ABCD中,O是AC和BD的交点.
(1)eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→))=________;
(2)eq \(AC,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(DO,\s\up6(→))=________;
(3)eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→))+eq \(CD,\s\up6(→))=________;
(4)eq \(AC,\s\up6(→))+eq \(BA,\s\up6(→))+eq \(DA,\s\up6(→))=________.
变式2:如图,在中,D为BC的中点,下列结论中正确的是( )
A.B.
C.D.
变式3:如图,四边形ABCD是平行四边形,则( )
A.B.C.D.
变式4:已知点O是的两条对角线的交点,则下面结论中正确的是( ).
A.B.
C.D.
变式5:如图,在中,为的中点,为上一点,则( )
A.B.C.D.
变式6:已知点D,E,F分别是△ABC各边的中点,则下列等式中错误的( )
A.B.
C.D.
变式7:在四边形ABCD中,eq \(AC,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→)),则( )
A.ABCD一定是矩形 B.ABCD一定是菱形
C.ABCD一定是正方形 D.ABCD一定是平行四边形
【例4】在矩形ABCD中,,,则向量的长度为( )
A.B.C.12D.6
变式1:如图所示,在正六边形ABCDEF中,若AB=1,则|AB+FE+CD|=( )
A.1B.2C.3D.23
向量加法的应用
要证四边形是平行四边形,只需证一组对边平行且相等.根据向量相等的意义,只需证其一组对边对应的向量相等即可.
【例5】用向量方法证明对角线互相平分的四边形是平行四边形.
向量加法的实际应用
向量应用题要首先画出图形.解决的步骤是:
1将应用问题中的量抽象成向量;
2化归为向量问题,进行向量运算;
3将向量问题还原为实际问题.
【例6】某人在静水中游泳,速度为4eq \r(3)千米/小时,他在水流速度为4千米/小时的河中游泳.他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度大小为多少?
变式1:一艘船以5 km/h的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成30°角,求水流速度和船实际速度.
考点二 向量的减法运算
相反向量
【例7】若非零向量和互为相反向量,则下列说法中错误的是( ).
A.B.C.D.
变式1:向量,互为相反向量,已知,则下列结论正确的是( )
A.B.为实数0C.与方向相同D.
变式2:如图,在四边形中,与交于点,若,则下面互为相反向量的是( )
A.与B.与C.与D.与
向量的减法法则
1.作两向量的差的步骤
eq \x(移)—eq \x(平移向量使之共起点)
↓
eq \x(连)—eq \x(连接两向量的终点,方向指向被减向量.)
2.求两个向量的减法的注意点
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后用加法a+(-b)即可.
(2)向量减法的三角形法则对共线向量也适用.
【例8】如图,在各小题中,已知,分别求作.
变式1:如图,已知向量a,b,c,求作a-b-c.
向量的减法运算
1首尾相接且为和;2起点相同且为差.,做题时要注意观察是否有这两种形式.同时要注意逆向应用,统一向量起点方法的应用.
【例9】化简eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))+eq \(CD,\s\up6(→))-eq \(AB,\s\up6(→))得( )
A.eq \(AB,\s\up6(→)) B.eq \(AD,\s\up6(→)) C.eq \(BC,\s\up6(→)) D.0
变式1:化简:(1)(eq \(AB,\s\up6(→))+eq \(MB,\s\up6(→)))+(-eq \(OB,\s\up6(→))-eq \(MO,\s\up6(→))); (2)eq \(AB,\s\up6(→))-eq \(AD,\s\up6(→))-eq \(DC,\s\up6(→)).
变式2:化简下列各式:
①;②;③;④.
其中结果为的个数是( )
A.1B.2C.3D.4
变式3:下列四式不能化简为的是( )
A. B. C. D.
【例10】在正方形中,( )
A.B.C.D.
变式1:在五边形中(如图),( )
A.B.C.D.
变式2:在五边形中(如图),下列运算结果为的是( )
A.B.
C.D.
变式3:如右图,,,分别是的边,,的中点,则( )
A.B.
C.D.
(三)向量减法的应用
【例11】已知正方形的边长为1,,,,则等于( )
A.0B.1C.D.2
【例12】在中,若,则的形状为( )
A.等边三角形B.等腰三角形
C.直角三角形D.等腰直角三角形
变式1:已知△OAB中,eq \(OA,\s\up7(→))=a,eq \(OB,\s\up7(→))=b,满足|a|=|b|=|a-b|=2,求|a+b|与△OAB的面积.
变式2:已知非零向量a,b满足|a|=eq \r(7)+1,|b|=eq \r(7)-1,且|a-b|=4,则|a+b|的值为 .
第四关
巩固练习识梳理
练习一 向量的加法运算
1、如图,已知向量a、b,求作向量a+b.
2、化简(1)eq \(BC,\s\up10(→))+eq \(AB,\s\up10(→)); (2)eq \(AO,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(OB,\s\up10(→)); (3)eq \(AB,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(FA,\s\up10(→)).
(4)eq \(DB,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→)); (5)(eq \(AB,\s\up10(→))+eq \(MB,\s\up10(→)))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→)).
3、向量化简后等于( )
A.B.C.D.
4、向量化简后等于( )
A.B.C.D.
5、向量化简后等于( )
A.B.C.D.
6、在平行四边形中,等于( )
A.B.C.D.
7、如图所示,点O是正六边形的中心,则( )
A.B.0C.D.
8、如图,已知O为正六边形ABCDEF的中心,求下列向量:
①eq \(OA,\s\up6(→))+eq \(OE,\s\up6(→)); ②eq \(AO,\s\up6(→))+eq \(AB,\s\up6(→)); ③eq \(AE,\s\up6(→))+eq \(AB,\s\up6(→)).
9、已知正方形的边长为,设,,,则等于( ).
A.B.C.D.
10、在四川5·12大地震后,一架救援直升飞机从A地沿北偏东60°方向飞行了40 km到B地,再由B地沿正北方向飞行40 km到达C地,求此时直升飞机与A地的相对位置.
练习二 向量的减法运算
1、如图,已知向量,,求作向量.
2、化简(1)(eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→)))-(eq \(AC,\s\up10(→))-eq \(BD,\s\up10(→))) (2)eq \(OA,\s\up6(→))-eq \(OD,\s\up6(→))+eq \(AD,\s\up6(→));(3)eq \(AB,\s\up6(→))+eq \(DA,\s\up6(→))+eq \(BD,\s\up6(→))-eq \(BC,\s\up6(→))-eq \(CA,\s\up6(→)).
3、化简得( )
A. B. C.D.
4、在△ABC中,eq \(BC,\s\up7(→))=a,eq \(CA,\s\up7(→))=b,则eq \(AB,\s\up7(→))等于( )
A.a+b B.-a+(-b) C.a-bD.b-a
5、在平行四边形ABCD中,( )
A.B.C.D.
6、(多选)若a,b为非零向量,则下列命题正确的是( )
A.若|a|+|b|=|a+b|,则a与b方向相同
B.若|a|+|b|=|a-b|,则a与b方向相反
C.若|a|+|b|=|a-b|,则|a|=|b|
D.若||a|-|b||=|a-b|,则a与b方向相同
7、在△ABC中,|eq \(AB,\s\up7(→))|=|eq \(BC,\s\up7(→))|=|eq \(CA,\s\up7(→))|=1,则|eq \(AB,\s\up7(→))-eq \(BC,\s\up7(→))|=________.
向量运算
定义
法则(或几何意义)
加法
求两个向量和的运算
向量加法的三角形法则:
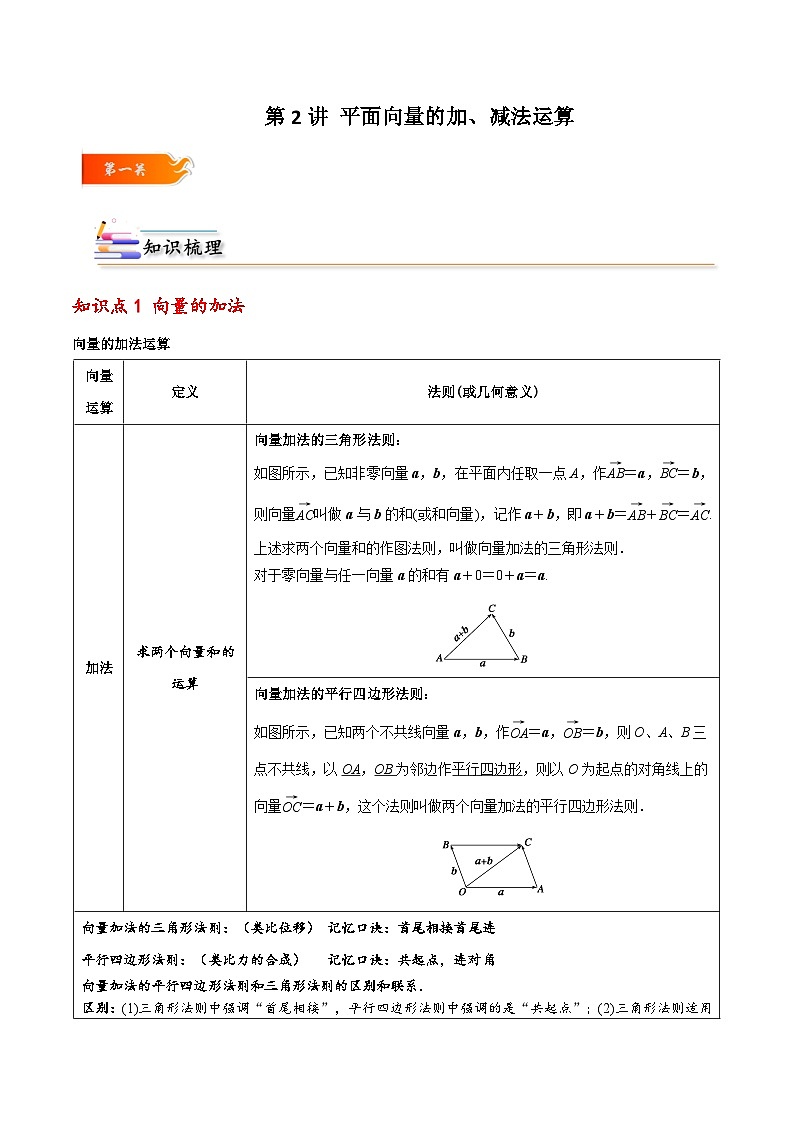
如图所示,已知非零向量a,b,在平面内任取一点A,作eq \(AB,\s\up6(→))=a,eq \(BC,\s\up6(→))=b,则向量eq \(AC,\s\up6(→))叫做a与b的和(或和向量),记作a+b,即a+b=eq \(AB,\s\up6(→))+eq \(BC,\s\up6(→))=eq \(AC,\s\up6(→)).上述求两个向量和的作图法则,叫做向量加法的三角形法则.21·世纪*
对于零向量与任一向量a的和有a+0=0+a=a.
向量加法的平行四边形法则:
如图所示,已知两个不共线向量a,b,作eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,则O、A、B三点不共线,以OA,OB为邻边作平行四边形,则以O为起点的对角线上的向量eq \(OC,\s\up6(→))=a+b,这个法则叫做两个向量加法的平行四边形法则.
www -2-
向量加法的三角形法则:(类比位移) 记忆口诀:首尾相接首尾连
平行四边形法则:(类比力的合成) 记忆口诀:共起点,连对角
向量加法的平行四边形法则和三角形法则的区别和联系.
区别:(1)三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;(2)三角形法则适用于任意两个非零向量求和(当两个向量共线时,三角形法则同样适用),而平行四边形法则仅适用于不共线的两个向量求和.
联系:(1)当两个向量不共线时,向量加法的三角形法则和平行四边形法则是统一的;
(2)三角形法则作出的图形是平行四边形法则作出的图形的一半.
向量加法的运算律: 交换律:; 结合律:.
和向量的模与原向量之间的关系:一般地,我们有.
当与共线且同向时,;
当与共线且异向时,;
当与不共线时,.
向量运算
定义
法则(或几何意义)
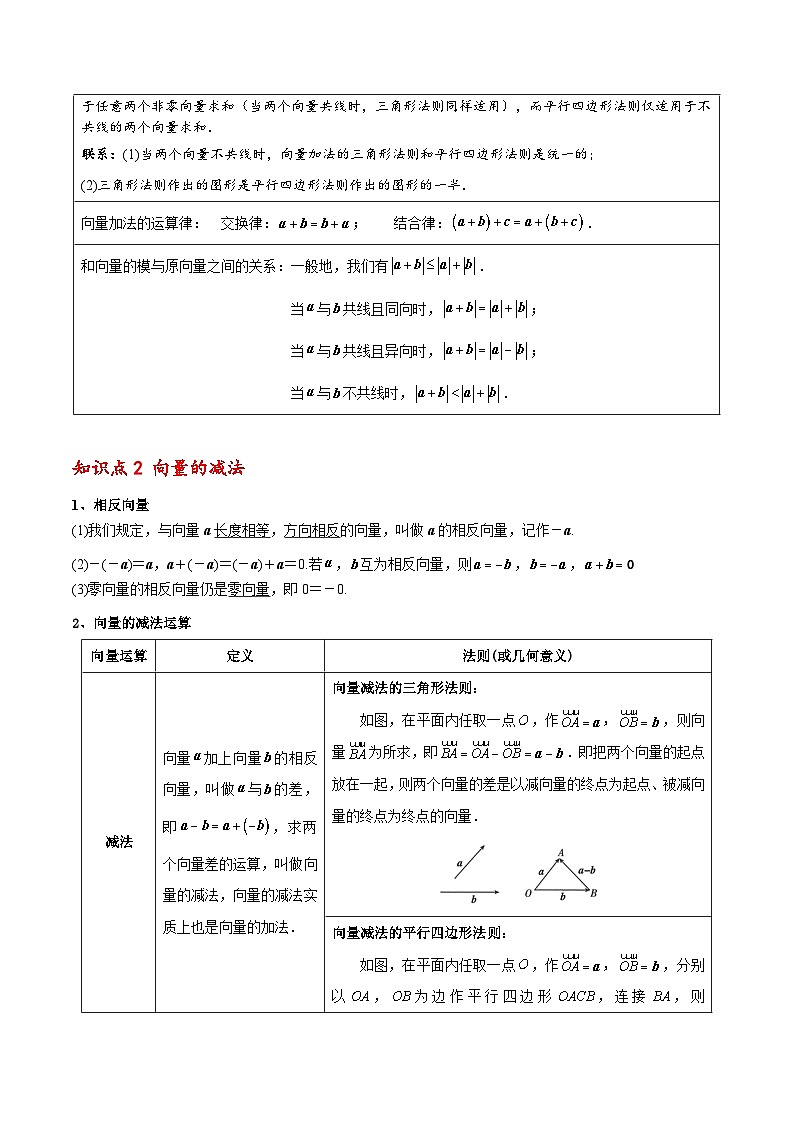
减法
向量加上向量的相反向量,叫做与的差,即,求两个向量差的运算,叫做向量的减法,向量的减法实质上也是向量的加法.
向量减法的三角形法则:
如图,在平面内任取一点,作,,则向量为所求,即.即把两个向量的起点放在一起,则两个向量的差是以减向量的终点为起点、被减向量的终点为终点的向量.
向量减法的平行四边形法则:
如图,在平面内任取一点,作,,分别以,为边作平行四边形,连接,则,这种作差向量的方法实质上是利用向量减法的定义.
向量减法的三角形法则:记忆口诀:首同尾连指被减
向量的加法和减法的运算问题
关于向量的加法和减法运算问题,一种解法就是依据三角形法则通过作图来解决,另一种解法就是通过表示向量的有向线段的字母符号运算来解决.具体地说,在一个用有向线段表示向量的运算式子中,将式子中的“−”改为“+”只需把表示向量的两个字母的顺序颠倒一下即可.如“”改为“”.解用几个基本向量表示某向量问题的基本技巧是,第一步:观察各向量位置;第二步:寻找(或作)相应的平行四边形或三角形:第三步:运用法则找关系;第四步:化简结果.
第2讲 平面向量的加、减法运算
知识点1 向量的加法
向量的加法运算
知识点2 向量的减法
1、相反向量
(1)我们规定,与向量a长度相等,方向相反的向量,叫做a的相反向量,记作-a.
(2)-(-a)=a,a+(-a)=(-a)+a=0.若,互为相反向量,则,,0
(3)零向量的相反向量仍是零向量,即0=-0.
2、向量的减法运算
考点一 向量的加法运算
解题方略
(1)平行四边形法则的应用前提:两个向量是从同一点出发的不共线向量.
三角形法则应用的前提:两个向量“首尾相接”.
当两个向量不共线时,三角形法则和平行四边形法则实质是一样的.三角形法则作出的图形是平行四边形法则作出图形的一半.但当两个向量共线时,平行四边形法则便不再适用.
向量的加法法则
已知向量a与向量b,要作出和向量a+b,关键是准确规范地依据向量的三角形法则和平行四边形法则作图.
【例1】如图,已知向量,,求作向量.
【解析】(1)平移,使其起点与起点重合,再应用平行四边形法则,作出,如下图示:
(2)平移,使其终点与起点重合,再以的起点为起点,的终点为终点作,如下图示:
变式1:如图,在下列各小题中,已知向量、,分别用两种方法求作向量.
【解析】将的起点移到的终点,再首尾相接,可得;
将两个向量的起点移到点,利用平行四边形法则,以、为邻边,作出平行四边形,则过点的对角线为向量.如图所示,.
(1);
(2);
(3) ;
(4).
向量的加法运算
在向量的加法运算中,通过向量加法的交换律,使各向量“首尾相连”,通过加法的结合律调整向量相加的顺序,可以省去画图步骤,加快解题速度.
【例2】化简:(1)eq \(BC,\s\up6(→))+eq \(AB,\s\up6(→)); (2)eq \(DB,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→)); (3)eq \(AB,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(FA,\s\up6(→)).
【解析】(1)eq \(BC,\s\up6(→))+eq \(AB,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(BC,\s\up6(→))=eq \(AC,\s\up6(→)).
(2)eq \(DB,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))=eq \(BC,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(DB,\s\up6(→))
=(eq \(BC,\s\up6(→))+eq \(CD,\s\up6(→)))+eq \(DB,\s\up6(→))=eq \(BD,\s\up6(→))+eq \(DB,\s\up6(→))=0.
(3)eq \(AB,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(FA,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(BC,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(FA,\s\up6(→))
=eq \(AC,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(FA,\s\up6(→))=eq \(AD,\s\up6(→))+eq \(DF,\s\up6(→))+eq \(FA,\s\up6(→))=eq \(AF,\s\up6(→))+eq \(FA,\s\up6(→))=0.
变式1:向量﹒化简后等于( )
A.B.0C.D.
【解析】
, 故选D.
变式2:化简下列各式:①;②;③;④.其中结果为的个数是( )
A.1B.2C.3D.4
【解析】对于①:,
对于②:,
对于③:,
对于④:,
所以结果为的个数是,
故选:B
变式3:已知、是不平行的向量,若,,,则下列关系中正确的是( )
A. B. C. D.
【解析】=++===2.故选:C
【例3】已知正六边形,则 ( )
A.B.C.D.
【解析】因为正六边形,所以,所以.
故选:C
变式1:如图,在平行四边形ABCD中,O是AC和BD的交点.
(1)eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→))=________;
(2)eq \(AC,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(DO,\s\up6(→))=________;
(3)eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→))+eq \(CD,\s\up6(→))=________;
(4)eq \(AC,\s\up6(→))+eq \(BA,\s\up6(→))+eq \(DA,\s\up6(→))=________.
【解析】(1)eq \(AC,\s\up6(→)) (2)eq \(AO,\s\up6(→)) (3)eq \(AD,\s\up6(→)) (4)
变式2:如图,在中,D为BC的中点,下列结论中正确的是( )
A.B.
C.D.
【解析】对于A,大小不相等,分向不相同,故不是相等向量,故A错误;
对于B,大小不相等,分向相反,是相反向量,故B错误;
对于C,利用三角形法则知,故C错误;
对于D,利用三角形法则知,故D正确;
故选:D
变式3:如图,四边形ABCD是平行四边形,则( )
A.B.C.D.
【解析】如图,设交于点,则.
故选:D
变式4:已知点O是的两条对角线的交点,则下面结论中正确的是( ).
A.B.
C.D.
【解析】对于A:,故A错误;
对于B:,故B正确;
对于C:,故C错误;
对于D:,故D错误;
故选:B
变式5:如图,在中,为的中点,为上一点,则( )
A.B.C.D.
【解析】因为为的中点,所以.
故选:A
变式6:已知点D,E,F分别是△ABC各边的中点,则下列等式中错误的( )
A.B.
C.D.
【解析】由题意,根据向量的加法运算法则,可得,故A正确;
由,故B正确;
根据平行四边形法则,可得,故C正确,D不正确.故选:D.
变式7:在四边形ABCD中,eq \(AC,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→)),则( )
A.ABCD一定是矩形 B.ABCD一定是菱形
C.ABCD一定是正方形 D.ABCD一定是平行四边形
【解析】由eq \(AC,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(AD,\s\up6(→))知,由A,B,C,D构成的四边形一定是平行四边形.
【例4】在矩形ABCD中,,,则向量的长度为( )
A.B.C.12D.6
【解析】因为,
所以的长度为的模的2倍.
又,
所以向量的长度为
故选:B
变式1:如图所示,在正六边形ABCDEF中,若AB=1,则|AB+FE+CD|=( )
A.1B.2C.3D.23
【解析】由题,可知FE=BC,所以|AB+FE+CD|=|AB+BC+CD|=|AD|=2.故选B.
向量加法的应用
要证四边形是平行四边形,只需证一组对边平行且相等.根据向量相等的意义,只需证其一组对边对应的向量相等即可.
【例5】用向量方法证明对角线互相平分的四边形是平行四边形.
证明:如图,根据向量加法的三角形法则有eq \(AB,\s\up6(→))=eq \(AO,\s\up6(→))+eq \(OB,\s\up6(→)),eq \(DC,\s\up6(→))=eq \(DO,\s\up6(→))+eq \(OC,\s\up6(→)).
又∵eq \(AO,\s\up6(→))=eq \(OC,\s\up6(→)),eq \(DO,\s\up6(→))=eq \(OB,\s\up6(→)),
∴eq \(AO,\s\up6(→))+eq \(OB,\s\up6(→))=eq \(DO,\s\up6(→))+eq \(OC,\s\up6(→)).
∴eq \(AB,\s\up6(→))=eq \(DC,\s\up6(→)).
∴AB∥DC且AB=DC,即AB与DC平行且相等.
∴四边形ABCD是平行四边形.
向量加法的实际应用
向量应用题要首先画出图形.解决的步骤是:
1将应用问题中的量抽象成向量;
2化归为向量问题,进行向量运算;
3将向量问题还原为实际问题.
【例6】某人在静水中游泳,速度为4eq \r(3)千米/小时,他在水流速度为4千米/小时的河中游泳.他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度大小为多少?
【解析】如图,设此人的实际速度为eq \(OD,\s\up6(→)),水流速度为eq \(OA,\s\up6(→)),游速为eq \(OB,\s\up6(→)),则eq \(OA,\s\up6(→))+eq \(OB,\s\up6(→))=eq \(OD,\s\up6(→)),在Rt△AOD中,|eq \(AD,\s\up6(→))|=4eq \r(3),|eq \(OA,\s\up6(→))|=4,则|eq \(OD,\s\up6(→))|=4eq \r(2),cs∠DAO=eq \f(\r(3),3).故此人沿向量eq \(OB,\s\up6(→))的方向游(即逆着水流且与河岸所成夹角的余弦值为eq \f(\r(3),3)),实际前进的速度大小为4eq \r(2)千米/小时.
变式1:一艘船以5 km/h的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成30°角,求水流速度和船实际速度.
【解析】如图所示,eq \(OA,\s\up6(→))表示水流速度,eq \(OB,\s\up6(→))表示船垂直于对岸的方向行驶的速度,eq \(OC,\s\up6(→))表示船实际航行的速度,∠AOC=30°,|eq \(OB,\s\up6(→))|=5..∵四边形OACB为矩形,
∴|eq \(OA,\s\up6(→))|=eq \f(|\(AC,\s\up6(→))|,tan 30°)=5eq \r(3),|eq \(OC,\s\up6(→))|=eq \f(|\(OB,\s\up6(→))|,sin 30°)=10,
∴水流速度大小为5eq \r(3) km/h,船实际速度为10 km/h.
考点二 向量的减法运算
相反向量
【例7】若非零向量和互为相反向量,则下列说法中错误的是( ).
A.B.C.D.
【解析】由平行向量的定义可知项正确;因为和的方向相反,所以,故项正确;
由相反向量的定义可知,故选项正确;由相反向量的定义知,故项错误;
故选:C.
变式1:向量,互为相反向量,已知,则下列结论正确的是( )
A.B.为实数0C.与方向相同D.
【解析】向量,互为相反向量,则,模相等、方向相反,所以,故A错误;
,故B错误;与方向相反,故C错误;,故D正确.
故选:D.
变式2:如图,在四边形中,与交于点,若,则下面互为相反向量的是( )
A.与B.与C.与D.与
【解析】因为,所以四边形是平行四边形,
所以,互相平分,所以,即与为相反向量.
故选:B
向量的减法法则
1.作两向量的差的步骤
eq \x(移)—eq \x(平移向量使之共起点)
↓
eq \x(连)—eq \x(连接两向量的终点,方向指向被减向量.)
2.求两个向量的减法的注意点
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后用加法a+(-b)即可.
(2)向量减法的三角形法则对共线向量也适用.
【例8】如图,在各小题中,已知,分别求作.
【解析】将的起点移到同一点,再首尾相接,方向指向被减向量,
如图,,
(1) (2)
(3) (4)
变式1:如图,已知向量a,b,c,求作a-b-c.
【解析】如图,以A为起点分别作向量eq \(AB,\s\up6(→))和eq \(AC,\s\up6(→)),使eq \(AB,\s\up6(→))=a,eq \(AC,\s\up6(→))=B.连接CB,得向量eq \(CB,\s\up6(→)),再以点C为起点作向量eq \(CD,\s\up6(→)),使eq \(CD,\s\up6(→))=c.连接DB,得向量eq \(DB,\s\up6(→)).则向量eq \(DB,\s\up6(→))即为所求作的向量a-b-c.
向量的减法运算
1首尾相接且为和;2起点相同且为差.,做题时要注意观察是否有这两种形式.同时要注意逆向应用,统一向量起点方法的应用.
【例9】化简eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))+eq \(CD,\s\up6(→))-eq \(AB,\s\up6(→))得( )
A.eq \(AB,\s\up6(→)) B.eq \(AD,\s\up6(→)) C.eq \(BC,\s\up6(→)) D.0
【解析】(1)解法一:eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))+eq \(CD,\s\up6(→))-eq \(AB,\s\up6(→))=eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BA,\s\up6(→))
=(eq \(AC,\s\up6(→))+eq \(CD,\s\up6(→)))+(eq \(BA,\s\up6(→))-eq \(BD,\s\up6(→)))=eq \(AD,\s\up6(→))+eq \(DA,\s\up6(→))=0.
解法二:eq \(AC,\s\up6(→))-eq \(BD,\s\up6(→))+eq \(CD,\s\up6(→))-eq \(AB,\s\up6(→))=eq \(AC,\s\up6(→))+eq \(DB,\s\up6(→))+eq \(CD,\s\up6(→))+eq \(BA,\s\up6(→))
=(eq \(AC,\s\up6(→))+eq \(CD,\s\up6(→)))+(eq \(DB,\s\up6(→))+eq \(BA,\s\up6(→)))=eq \(AD,\s\up6(→))+eq \(DA,\s\up6(→))=0.
变式1:化简:(1)(eq \(AB,\s\up6(→))+eq \(MB,\s\up6(→)))+(-eq \(OB,\s\up6(→))-eq \(MO,\s\up6(→))); (2)eq \(AB,\s\up6(→))-eq \(AD,\s\up6(→))-eq \(DC,\s\up6(→)).
【解析】(1)解法一:原式=eq \(AB,\s\up6(→))+eq \(MB,\s\up6(→))+eq \(BO,\s\up6(→))+eq \(OM,\s\up6(→))
=(eq \(AB,\s\up6(→))+eq \(BO,\s\up6(→)))+(eq \(OM,\s\up6(→))+eq \(MB,\s\up6(→)))=eq \(AO,\s\up6(→))+eq \(OB,\s\up6(→))=eq \(AB,\s\up6(→)).
解法二:原式=eq \(AB,\s\up6(→))+eq \(MB,\s\up6(→))-eq \(OB,\s\up6(→))-eq \(MO,\s\up6(→))
=eq \(AB,\s\up6(→))+(eq \(MB,\s\up6(→))-eq \(MO,\s\up6(→)))-eq \(OB,\s\up6(→))=eq \(AB,\s\up6(→))+(eq \(OB,\s\up6(→))-eq \(OB,\s\up6(→)))
=eq \(AB,\s\up6(→))+0=eq \(AB,\s\up6(→)).
(2)解法一:原式=eq \(DB,\s\up6(→))-eq \(DC,\s\up6(→))=eq \(CB,\s\up6(→)).
解法二:原式=eq \(AB,\s\up6(→))-(eq \(AD,\s\up6(→))+eq \(DC,\s\up6(→)))=eq \(AB,\s\up6(→))-eq \(AC,\s\up6(→))=eq \(CB,\s\up6(→)).
变式2:化简下列各式:
①;②;③;④.
其中结果为的个数是( )
A.1B.2C.3D.4
【解析】①;
②;
③;
④;
以上各式化简后结果均为,故选:D
变式3:下列四式不能化简为的是( )
A. B. C. D.
【解析】A项中,;
B项中,;
C项中,;
D项中,.
故选:D.
【例10】在正方形中,( )
A.B.C.D.
【解析】.故选:C.
变式1:在五边形中(如图),( )
A.B.C.D.
【解析】.故选:B
变式2:在五边形中(如图),下列运算结果为的是( )
A.B.
C.D.
【解析】A,,正确;
B,,不正确;
C,,不正确;
D,, 不正确.
故选:A.
变式3:如右图,,,分别是的边,,的中点,则( )
A.B.
C.D.
【解析】,故A正确;
,故B错误;
,故C错误;
,故D错误.
故选:A.
(三)向量减法的应用
【例11】已知正方形的边长为1,,,,则等于( )
A.0B.1C.D.2
【解析】因为,,,所以.
故选:A.
【例12】在中,若,则的形状为( )
A.等边三角形B.等腰三角形
C.直角三角形D.等腰直角三角形
【解析】因为,,
所以,所以为等边三角形.
故选:A.
变式1:已知△OAB中,eq \(OA,\s\up7(→))=a,eq \(OB,\s\up7(→))=b,满足|a|=|b|=|a-b|=2,求|a+b|与△OAB的面积.
【解析】由已知得|eq \(OA,\s\up7(→))|=|eq \(OB,\s\up7(→))|,以eq \(OA,\s\up7(→)),eq \(OB,\s\up7(→))为邻边作平行四边形OACB,则可知其为菱形,且eq \(OC,\s\up7(→))=a+b,eq \(BA,\s\up7(→))=a-b,由于|a|=|b|=|a-b|,则OA=OB=BA,
∴△OAB为正三角形,
∴|a+b|=|eq \(OC,\s\up7(→))|=2×eq \r(3)=2eq \r(3),
S△OAB=eq \f(1,2)×2×eq \r(3)=eq \r(3).
变式2:已知非零向量a,b满足|a|=eq \r(7)+1,|b|=eq \r(7)-1,且|a-b|=4,则|a+b|的值为 .
【解析】如图,令eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,则|eq \(BA,\s\up6(→))|=|a-b|.
以OA与OB为邻边作平行四边形OACB,则|eq \(OC,\s\up6(→))|=|a+b|.由于(eq \r(7)+1)2+(eq \r(7)-1)2=42.故|eq \(OA,\s\up6(→))|2+|eq \(OB,\s\up6(→))|2=|eq \(BA,\s\up6(→))|2,所以△OAB是∠AOB为90°的直角三角形,从而OA⊥OB,所以平行四边形OACB是矩形.根据矩形的对角线相等有|eq \(OC,\s\up6(→))|=|eq \(BA,\s\up6(→))|=4,即|a+b|=4.
第四关
巩固练习识梳理
练习一 向量的加法运算
1、如图,已知向量a、b,求作向量a+b.
【解析】在平面内任取一点O(如下图),作eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,以OA、OB为邻边做▱OACB,连接OC,则eq \(OC,\s\up6(→))=eq \(OA,\s\up6(→))+eq \(OB,\s\up6(→))=a+b.2
2、化简(1)eq \(BC,\s\up10(→))+eq \(AB,\s\up10(→)); (2)eq \(AO,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(OB,\s\up10(→)); (3)eq \(AB,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(FA,\s\up10(→)).
(4)eq \(DB,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→)); (5)(eq \(AB,\s\up10(→))+eq \(MB,\s\up10(→)))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→)).
【解析】 (1)eq \(BC,\s\up10(→))+eq \(AB,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(BC,\s\up10(→))=eq \(AC,\s\up10(→)).
(2)eq \(AO,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(OB,\s\up10(→))=eq \(AO,\s\up10(→))+eq \(OB,\s\up10(→))+eq \(BC,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(BC,\s\up10(→))=eq \(AC,\s\up10(→)).
(3)eq \(AB,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(FA,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(BC,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(FA,\s\up10(→))=eq \(AC,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(FA,\s\up10(→))=eq \(AD,\s\up10(→))+eq \(DF,\s\up10(→))+eq \(FA,\s\up10(→))=eq \(AF,\s\up10(→))+eq \(FA,\s\up10(→))=0.
(4)eq \(DB,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(BC,\s\up10(→))=eq \(BC,\s\up10(→))+eq \(CD,\s\up10(→))+eq \(DB,\s\up10(→))=eq \(BD,\s\up10(→))+eq \(DB,\s\up10(→))=0.
(5)方法一 (eq \(AB,\s\up10(→))+eq \(MB,\s\up10(→)))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→))=(eq \(AB,\s\up10(→))+eq \(BO,\s\up10(→)))+(eq \(OM,\s\up10(→))+eq \(MB,\s\up10(→)))=eq \(AO,\s\up10(→))+eq \(OB,\s\up10(→))=eq \(AB,\s\up10(→)).
方法二 (eq \(AB,\s\up10(→))+eq \(MB,\s\up10(→)))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→))=eq \(AB,\s\up10(→))+(eq \(MB,\s\up10(→))+eq \(BO,\s\up10(→)))+eq \(OM,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(MO,\s\up10(→))+eq \(OM,\s\up10(→))=eq \(AB,\s\up10(→))+0=eq \(AB,\s\up10(→)).
方法三 (eq \(AB,\s\up10(→))+eq \(MB,\s\up10(→)))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→))=(eq \(AB,\s\up10(→))+eq \(BO,\s\up10(→))+eq \(OM,\s\up10(→)))+eq \(MB,\s\up10(→))=eq \(AM,\s\up10(→))+eq \(MB,\s\up10(→))=eq \(AB,\s\up10(→)).
3、向量化简后等于( )
A.B.C.D.
【解析】由,故选:A
4、向量化简后等于( )
A.B.C.D.
【解析】
故选:C.
5、向量化简后等于( )
A.B.C.D.
【解析】
.
故选:C.
6、在平行四边形中,等于( )
A.B.C.D.
【解析】画出图形,如图所示:
.
故选:A.
7、如图所示,点O是正六边形的中心,则( )
A.B.0C.D.
【解析】∵,∴,故选A.
8、如图,已知O为正六边形ABCDEF的中心,求下列向量:
①eq \(OA,\s\up6(→))+eq \(OE,\s\up6(→)); ②eq \(AO,\s\up6(→))+eq \(AB,\s\up6(→)); ③eq \(AE,\s\up6(→))+eq \(AB,\s\up6(→)).
【解析】①由题图知,OAFE为平行四边形,∴eq \(OA,\s\up6(→))+eq \(OE,\s\up6(→))=eq \(OF,\s\up6(→));
②由题图知,OABC为平行四边形,∴eq \(AO,\s\up6(→))+eq \(AB,\s\up6(→))=eq \(AC,\s\up6(→));
③由题图知,AEDB为平行四边形,∴eq \(AE,\s\up6(→))+eq \(AB,\s\up6(→))=eq \(AD,\s\up6(→)).
9、已知正方形的边长为,设,,,则等于( ).
A.B.C.D.
【解析】因为正方形的边长为,,,,
所以.故选:D
10、在四川5·12大地震后,一架救援直升飞机从A地沿北偏东60°方向飞行了40 km到B地,再由B地沿正北方向飞行40 km到达C地,求此时直升飞机与A地的相对位置.
【解析】如图所示,设eq \(AB,\s\up6(→))、eq \(BC,\s\up6(→))分别是直升飞机两次位移,则eq \(AC,\s\up6(→))表示两次位移的合位移,即eq \(AC,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(BC,\s\up6(→)),
在Rt△ABD中,|eq \(DB,\s\up6(→))|=20 km,|eq \(AD,\s\up6(→))|=20eq \r(3) km,
在Rt△ACD中,
|eq \(AC,\s\up6(→))|= eq \r(|\(AD,\s\up6(→))|2+|\(DC,\s\up6(→))|2)=40eq \r(3) km,
∠CAD=60°,即此时直升飞机位于A地北偏东30°,且距离A地40eq \r(3) km处.
练习二 向量的减法运算
1、如图,已知向量,,求作向量.
【解析】(1)如图,将向量的起点平移到向量的起点,
以向量的终点为起点,向量的终点为终点的向量即为向量;
(2)如图,将向量的起点平移到向量的起点,
以向量的终点为起点,向量的终点为终点的向量即为向量;
2、化简(1)(eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→)))-(eq \(AC,\s\up10(→))-eq \(BD,\s\up10(→))) (2)eq \(OA,\s\up6(→))-eq \(OD,\s\up6(→))+eq \(AD,\s\up6(→));(3)eq \(AB,\s\up6(→))+eq \(DA,\s\up6(→))+eq \(BD,\s\up6(→))-eq \(BC,\s\up6(→))-eq \(CA,\s\up6(→)).
【解析】(1)方法一(统一成加法) (eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→)))-(eq \(AC,\s\up10(→))-eq \(BD,\s\up10(→)))=eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→))-eq \(AC,\s\up10(→))+eq \(BD,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(DC,\s\up10(→))+eq \(CA,\s\up10(→))+eq \(BD,\s\up10(→))=eq \(AB,\s\up10(→))+eq \(BD,\s\up10(→))+eq \(DC,\s\up10(→))+eq \(CA,\s\up10(→))=eq \(AD,\s\up10(→))+eq \(DA,\s\up10(→))=0.
方法二(利用eq \(OA,\s\up10(→))-eq \(OB,\s\up10(→))=eq \(BA,\s\up10(→))) (eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→)))-(eq \(AC,\s\up10(→))-eq \(BD,\s\up10(→)))=eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→))-eq \(AC,\s\up10(→))+eq \(BD,\s\up10(→))=(eq \(AB,\s\up10(→))-eq \(AC,\s\up10(→)))-eq \(CD,\s\up10(→))+eq \(BD,\s\up10(→))=eq \(CB,\s\up10(→))-eq \(CD,\s\up10(→))+eq \(BD,\s\up10(→))=eq \(DB,\s\up10(→))+eq \(BD,\s\up10(→))=0.
方法三(利用eq \(AB,\s\up10(→))=eq \(OB,\s\up10(→))-eq \(OA,\s\up10(→))) 设O是平面内任意一点,则(eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→)))-(eq \(AC,\s\up10(→))-eq \(BD,\s\up10(→)))=eq \(AB,\s\up10(→))-eq \(CD,\s\up10(→))-eq \(AC,\s\up10(→))+eq \(BD,\s\up10(→))=(eq \(OB,\s\up10(→))-eq \(OA,\s\up10(→)))-(eq \(OD,\s\up10(→))-eq \(OC,\s\up10(→)))-(eq \(OC,\s\up10(→))-eq \(OA,\s\up10(→)))+(eq \(OD,\s\up10(→))-eq \(OB,\s\up10(→)))=eq \(OB,\s\up10(→))-eq \(OA,\s\up10(→))-eq \(OD,\s\up10(→))+eq \(OC,\s\up10(→))-eq \(OC,\s\up10(→))+eq \(OA,\s\up10(→))+eq \(OD,\s\up10(→))-eq \(OB,\s\up10(→))=0.
(2)eq \(OA,\s\up6(→))-eq \(OD,\s\up6(→))+eq \(AD,\s\up6(→))=eq \(OA,\s\up6(→))+eq \(AD,\s\up6(→))-eq \(OD,\s\up6(→))=eq \(OD,\s\up6(→))-eq \(OD,\s\up6(→))=0.
(3)eq \(AB,\s\up6(→))+eq \(DA,\s\up6(→))+eq \(BD,\s\up6(→))-eq \(BC,\s\up6(→))-eq \(CA,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(DA,\s\up6(→))+eq \(BD,\s\up6(→))+eq \(CB,\s\up6(→))+eq \(AC,\s\up6(→))=(eq \(AB,\s\up6(→))+eq \(BD,\s\up6(→)))+(eq \(AC,\s\up6(→))+eq \(CB,\s\up6(→)))+Deq \(A,\s\up6(→))=eq \(AD,\s\up6(→))+eq \(AB,\s\up6(→))+eq \(DA,\s\up6(→))=eq \(AD,\s\up6(→))+eq \(DA,\s\up6(→))+eq \(AB,\s\up6(→))=0+eq \(AB,\s\up6(→))=eq \(AB,\s\up6(→)).
3、化简得( )
A. B. C.D.
【解析】.
故选:A.
4、在△ABC中,eq \(BC,\s\up7(→))=a,eq \(CA,\s\up7(→))=b,则eq \(AB,\s\up7(→))等于( )
A.a+b B.-a+(-b) C.a-bD.b-a
【解析】如图,∵eq \(BA,\s\up7(→))=eq \(BC,\s\up7(→))+eq \(CA,\s\up7(→))=a+b,∴eq \(AB,\s\up7(→))=-eq \(BA,\s\up7(→))=-a-b.
5、在平行四边形ABCD中,( )
A.B.C.D.
【解析】如图:
在,由平面向量的三角形减法法则可得:,在平行四边形ABCD中,,所以.故选:A.
6、(多选)若a,b为非零向量,则下列命题正确的是( )
A.若|a|+|b|=|a+b|,则a与b方向相同
B.若|a|+|b|=|a-b|,则a与b方向相反
C.若|a|+|b|=|a-b|,则|a|=|b|
D.若||a|-|b||=|a-b|,则a与b方向相同
【解析】当a,b方向相同时,有|a|+|b|=|a+b|,||a|-|b||=|a-b|;当a,b方向相反时,有|a|+|b|=|a-b|,||a|-|b||=|a+b|,故A,B,D均正确.
7、在△ABC中,|eq \(AB,\s\up7(→))|=|eq \(BC,\s\up7(→))|=|eq \(CA,\s\up7(→))|=1,则|eq \(AB,\s\up7(→))-eq \(BC,\s\up7(→))|=________.
【解析】如图,延长CB到点D,使CB=BD,连接AD.
在△ABD中,AB=BD=1,
∠ABD=120°,
eq \(AB,\s\up7(→))-eq \(BC,\s\up7(→))=eq \(AB,\s\up7(→))+eq \(CB,\s\up7(→))
=eq \(AB,\s\up7(→))+eq \(BD,\s\up7(→))=eq \(AD,\s\up7(→)).
易求得AD=eq \r(3),
即|eq \(AD,\s\up7(→))|=eq \r(3).
所以|eq \(AB,\s\up7(→))-eq \(BC,\s\up7(→))|=eq \r(3).
向量运算
定义
法则(或几何意义)
加法
求两个向量和的运算
向量加法的三角形法则:
如图所示,已知非零向量a,b,在平面内任取一点A,作eq \(AB,\s\up6(→))=a,eq \(BC,\s\up6(→))=b,则向量eq \(AC,\s\up6(→))叫做a与b的和(或和向量),记作a+b,即a+b=eq \(AB,\s\up6(→))+eq \(BC,\s\up6(→))=eq \(AC,\s\up6(→)).上述求两个向量和的作图法则,叫做向量加法的三角形法则.21·世纪*
对于零向量与任一向量a的和有a+0=0+a=a.
向量加法的平行四边形法则:
如图所示,已知两个不共线向量a,b,作eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,则O、A、B三点不共线,以OA,OB为邻边作平行四边形,则以O为起点的对角线上的向量eq \(OC,\s\up6(→))=a+b,这个法则叫做两个向量加法的平行四边形法则.
www -2-
向量加法的三角形法则:(类比位移) 记忆口诀:首尾相接首尾连
平行四边形法则:(类比力的合成) 记忆口诀:共起点,连对角
向量加法的平行四边形法则和三角形法则的区别和联系.
区别:(1)三角形法则中强调“首尾相接”,平行四边形法则中强调的是“共起点”;(2)三角形法则适用于任意两个非零向量求和(当两个向量共线时,三角形法则同样适用),而平行四边形法则仅适用于不共线的两个向量求和.
联系:(1)当两个向量不共线时,向量加法的三角形法则和平行四边形法则是统一的;
(2)三角形法则作出的图形是平行四边形法则作出的图形的一半.
向量加法的运算律: 交换律:; 结合律:.
和向量的模与原向量之间的关系:一般地,我们有.
当与共线且同向时,;
当与共线且异向时,;
当与不共线时,.
向量运算
定义
法则(或几何意义)
减法
向量加上向量的相反向量,叫做与的差,即,求两个向量差的运算,叫做向量的减法,向量的减法实质上也是向量的加法.
向量减法的三角形法则:
如图,在平面内任取一点,作,,则向量为所求,即.即把两个向量的起点放在一起,则两个向量的差是以减向量的终点为起点、被减向量的终点为终点的向量.
向量减法的平行四边形法则:
如图,在平面内任取一点,作,,分别以,为边作平行四边形,连接,则,这种作差向量的方法实质上是利用向量减法的定义.
向量减法的三角形法则:记忆口诀:首同尾连指被减
向量的加法和减法的运算问题
关于向量的加法和减法运算问题,一种解法就是依据三角形法则通过作图来解决,另一种解法就是通过表示向量的有向线段的字母符号运算来解决.具体地说,在一个用有向线段表示向量的运算式子中,将式子中的“−”改为“+”只需把表示向量的两个字母的顺序颠倒一下即可.如“”改为“”.解用几个基本向量表示某向量问题的基本技巧是,第一步:观察各向量位置;第二步:寻找(或作)相应的平行四边形或三角形:第三步:运用法则找关系;第四步:化简结果.
高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02讲复数的几何意义(原卷版+解析): 这是一份高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02讲复数的几何意义(原卷版+解析),共35页。
高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02讲事件的关系和运算(原卷版+解析): 这是一份高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02讲事件的关系和运算(原卷版+解析),共23页。
高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02练平面向量的加、减法运算(原卷版+解析): 这是一份高一数学下学期考点精讲+精练(人教A版2019必修第二册)第02练平面向量的加、减法运算(原卷版+解析),共20页。试卷主要包含了等于,化简以下各式,在菱形中,下列式子成立的是,已知为的中线,则,在平行四边形中,,如图,在矩形中,等内容,欢迎下载使用。












