广东省深圳市福田区2023-2024学年七年级下学期期末数学试题

这是一份广东省深圳市福田区2023-2024学年七年级下学期期末数学试题，共10页。试卷主要包含了考生必须保证答题卡的整洁，下列说法正确的是等内容，欢迎下载使用。

本试题共6页，22题，满分100分，考试用时90分钟。
注意事项：
1.答卷前，考生务必将自己的姓名、考生号填写在答题卡上。将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑。如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按上述要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后，留存试卷，交回答题卡。
第一部分 选择题
一、选择题（本题共10小题，每小题3分，共30分.每小题给出4个选项，其中只有一个是正确的）
1.下列四幅作品分别代表二十四节气中的“春分”、“夏至”、“立秋”、“冬至”，其中是轴对称图形的是
A. B.C. D.
2.中国移动从深圳至东莞的空芯光纤传输技术试验网取得重大突破，在每公里的链路上，空芯-空芯光纤熔接损耗低至0.0025分贝，将数据0.0025用科学记数法表示为
A.B.C.D.
3.下列计算正确的是
A.B.C.D.
4.如图1，A，D，E三点共线，下列条件中能判断直线AD∥BC的是
A.∠1=∠2B.∠1=∠3
C.∠E=∠3D.∠D+∠1=180°
5.下列各式能直接用平方差公式计算的是
A.B.
C.D.
6.如图2，小英在池塘一侧选取了点O，测得OA=8m，OB=5m，那么池塘两岸A，B间的距离可能是
A.10mB.3mC.14mD.13m
7.在△ABC中，∠BAC为钝角，现利用一块含30°角的透明直角三角板，画AC边上的高，下列三角板摆放正确的是
A.B.C.D.
8.下列说法正确的是
A.两直线平行，同旁内角相等
B.抛一枚质地均匀的硬币正面朝上的概率是0.5，表示每抛硬币2次必有1次出现正面朝上
C.角平分线上的点到这个角的两边的距离相等
D.两边及一角分别相等的两个三角形全等
9.深圳地铁14号线，也称“深圳地铁东部快线”，它起于福田区岗厦北交通枢纽，途至坪山区沙田，采用自动化无人驾驶技术，全长50.34km，最高运行速度可达120km/h.如图3，为地铁14号线从黄木岗站到罗湖北站行驶的速度-时间图象，根据图象，下列分析错误的是
A.自变量是行驶时间，因变量是行驶速度
B.地铁加速用时比减速用时长
C.地铁匀速前进的时长为2.5min
D.在这段时间内地铁的最高运行速度为90km/h
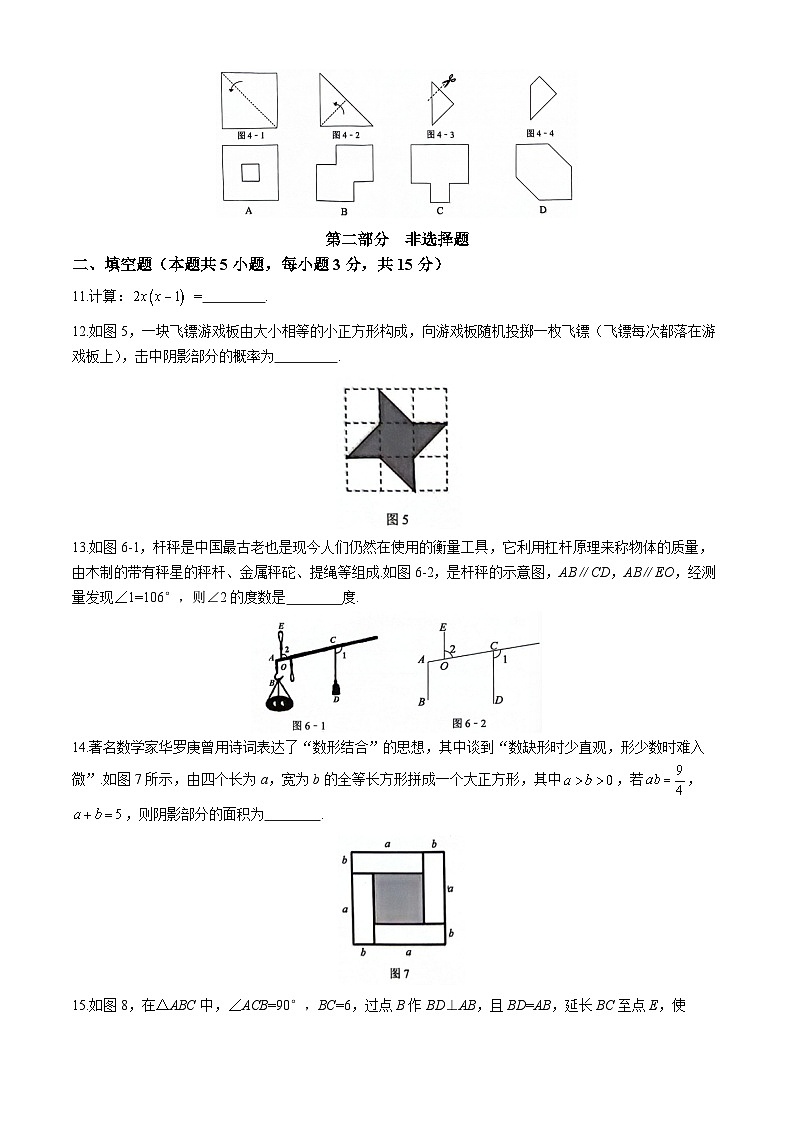
10.将一张正方形纸片按如图4-1，图4-2所示的方向对折得到图4-3，然后沿图4-3中的虚线剪裁得到图4-4，将图4-4的纸片展开铺平后得到的图案是
第二部分 非选择题
二、填空题（本题共5小题，每小题3分，共15分）
11.计算： = .
12.如图5，一块飞镖游戏板由大小相等的小正方形构成，向游戏板随机投掷一枚飞镖（飞镖每次都落在游戏板上），击中阴影部分的概率为 .
13.如图6-1，杆秤是中国最古老也是现今人们仍然在使用的衡量工具，它利用杠杆原理来称物体的质量，由木制的带有秤星的秤杆、金属秤砣、提绳等组成.如图6-2，是杆秤的示意图，AB∥CD，AB∥EO，经测量发现∠1=106°，则∠2的度数是 度.
14.著名数学家华罗庚曾用诗词表达了“数形结合”的思想，其中谈到“数缺形时少直观，形少数时难入微”.如图7所示，由四个长为a，宽为b的全等长方形拼成一个大正方形，其中，若，，则阴影部分的面积为 .
15.如图8，在△ABC中，∠ACB=90°，BC=6，过点B作BD⊥AB，且BD=AB，延长BC至点E，使，连接DE并延长交AC边于点F，若，则AC= .
三、解答题（本题共7小题，其中16题8分，17题6分，18题8分，19题8分，20题7分，21题9分，22题9分，共55分）
16.（8分）计算：（1）；
（2）.
17.（6分）先化简，再求值：，其中，.
18.（8分）阅读并完成下列推理过程，在括号中填写依据.
如图9，点B，D，C在同一直线上，，，∠A=∠CFD，CE=8，CF=3，求AF的长.
解：∵∠A=∠CFD（已知），
∴ ∥ （ ）.
∴∠B=∠CDE（ ）.
在△ABC和△CDE中，
∴△ABC≌△CDE（ ）.
∴ =CE（ ）.
∵CE=8（已知），
∴AC= .
∵CF=3（已知），
∴AF=8-3=5.
19.（8分）一个不透明的袋中只装有白、红、黄三种颜色的球共40个，它们除颜色外都完全相同，其中白球个数是黄球个数的2倍多1个.已知从袋中随机摸出一个球是红球的概率是.
（1）从袋中随机摸出一个球是黄球是 事件（从“随机”、“必然”、“不可能”选一个填入）；
（2）袋中有 个红球；
（3）求从袋中随机摸出一个球是黄球的概率.
20.（7分）如图10，在△ABC中，AB=AC.
（1）读下列语句，按要求用尺规作图（保留作图痕迹，不要求写作法）：
①分别以点A和C为圆心，以大于的长为半径作弧，两弧相交于点M和N；
②作直线MN，交线段AC于点E，交线段AB于点D.
（2）在（1）的条件下，连接CD，当∠A=42°时，求∠BCD的度数.
21.（9分）根据以下信息，探索完成任务：
22.（9分）综合与实践课上，李老师以“发现-探究-拓展”的形式，培养学生数学思想，训练学生数学思维.以下是李老师的课堂主题展示：
（1）如图，在等腰△ABC中，AC=BC，点D为线段AB上的一动点（点D不与A，B重合），以CD为边作等腰△CDE，CD=CE，∠ACB=∠DCE=，连接BE.解答下列问题：
【观察发现】
①如图11-1，当时，线段AD，BE的数量关系为 ，.∠ABE= °；
【类比探究】
②如图11-2，当时，试探究线段AC与BE的位置关系，并说明理由；
【拓展延伸】
（2）如图11-3，四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，连接AC，若AC=8，则四边形ABCD的面积为多少?（直接写出结果）.
2023—2024学年第二学期期末学业质量调研测试
七年级数学参考答案
一、选择题（本题共10小题，每小题3分，共30分）
二、填空题（本题共5小题，每小题3分，共15分）
11.；12.；13.74；14.16；15.12.
三、解答题（本题共7小题，其中16题8分，17题6分，18题8分，19题8分，20题7分，21题9分，22题9分，共55分）
16.（8分）计算：（1）（4分）
解：原式=﹣8+9﹣1……………………………………………………………………1+1+1分，累计3分
=0………………………………………………………………1分，累计4分
（2）（4分）计算：
解：原式＝9x4y2•（﹣2xy3）÷（﹣6x4y5）…………………………………………………2分
＝﹣18x5y5÷（﹣6x4y5）…………………………………………………………………1分，累计3分
＝3x…………………………………………………………………1分，累计4分
17.（6分）先化简，再求值：，其中，．
解：原式＝[4x2﹣4xy+y2﹣（4x2﹣y2）]÷（﹣2y）…………………………………………2分
＝（﹣4xy+2y2）÷（﹣2y）…………………………………………………1分，累计3分
＝2x﹣y…………………………………………………1分，累计4分
将x＝﹣，y＝2代入得，
原式＝＝．…………………………………………………2分，累计6分
18.（8分）解：∵∠A＝∠CFD（已知），
∴ AB ∥ DE （同位角相等，两直线平行）
∴∠B＝∠CDE（两直线平行，同位角相等），
在△ABC和△CDE中，
∴△ABC≌△CDE（ SAS ）．
∴ AC ＝CE（全等三角形对应边相等）．
∵CE＝8（已知），
∴AC= 8
∵CF＝3（已知），
∴AF＝ACCF＝83＝5．
（说明：每空1分）…………………………………………………………………累计8分
19.（8分）解：（1）从袋中随机摸出一个球是黄球是随机事件；…………………………………………2分
（2）袋中有 24 个红球；…………………………………………2分，累计4分
根据题意得：40×＝24（个），答：袋中红球的个数有24个．
（3）设黄球有x个，则白球有（2x+1）个，
根据题意得x+2x+1＝40﹣24………………………………………………………1分，累计5分
解得x＝5．………………………………………………………1分，累计6分
从袋中任摸一个球共有40种等可能得结果，其中摸出黄球有5种，
∴P（摸出黄球）=
答：摸出一个球是黄球的概率是……………………………………………2分，累计8分
【说明：用“P（摸出黄球）”才能得2分，缺失（），只写P只能得1分】
20.（7分）解：（1）如图所示：直线DE即为所求（直线MN即为所求）；
（说明：作图要有痕迹且正确得2分，书写结论1分）………………2+1分，累计3分
（2）∵AB＝AC，∠A＝42°，
∴∠ACB＝∠B＝（180°﹣42°）＝69°，………………………………………1分，累计4分
∵DE垂直平分AC，
∴AD＝DC，………………………………………………1分，累计5分
∴∠ACD＝∠A＝42°，………………………………………………1分，累计6分
∴∠BCD＝∠ACB﹣∠ACD＝69°﹣42°＝27°．…………………………………1分，累计7分
21.（9分）解：
任务一：某用户选择中国移动B套餐，
若该月拨打国内电话时长为200分钟，则该用户的月缴费为 88 元；
若该月拨打国内电话时长为380分钟，则该用户的月缴费为 93.7 元．
……………………………………………………………………………………………1+1分，累计2分
任务二：若选择A套餐计费方法，设某用户一个月的拨打国内电话时长为x分钟（x>150），
该月话费为元，则与x的关系式是y1=58+0.19（x-150）或y1=0.19x+29.5；
若选择B套餐计费方法，设某用户一个月的拨打国内电话时长为x分钟（x>350），
该月话费为元，则与x的关系式是y2=88+0.19（x-350）或y2=0.19x+21.5．
……………………………………………………………………………………………2+2分，累计6分
任务三：∵150＜250＜350
∴当x=250时，y1=0.19×250+29.5=77…………………………………………………1分，累计7分
y2=88……………………………………………………………1分，累计8分
∵y1＜y2
∴选择A套餐比较划算.……………………………………………………………1分，累计9分
22.（9分）解：
（1）【观察发现】
①线段AD，BE的数量关系为 AD=BE （或相等），
∠ABE＝ 90 °；…………………1+1分，累计2分
【类比探究】
图1
②AC∥BE，………………………………………………1分，累计3分
理由如下：
∵∠ACB=∠DCE=60°
∴∠ACB-∠DCB=∠DCE-∠DCB
即∠ACD=∠BCE………………………………………………1分，累计4分
∵CA=CB
∴∠A=∠CBA=（180°-60°）=60°………………………………………………1分，累计5分
在△ACD和△BCE中，
∴△ACD≌△BCE（SAS）………………………………………………1分，累计6分
∴∠A=∠CBE=60°
∴∠ACB=∠CBE
∴AC∥BE………………………………………………1分，累计7分
【拓展延伸】
（2）32………………………………………………2分，累计9分
如图2，过A作AG⊥AC交CB延长线于G，
图2
∵∠ABC+∠ACB+∠BAC=180°，∠ACD+∠CDA+∠CAD=180°
∴∠ABC+∠BCD+∠CDA+∠DAB=360°
∵∠BAD=∠BCD=90°
∴∠ABC+∠ADC=180°
又∵∠ABC+∠ABG=180°
∴∠ADC=∠ABG
∵∠DAB=∠CAG=90°
∴∠DAB-∠BAC=∠CAG-∠BAC
即∠DAC=∠BAG
在△ACD和△AGB中，
∴△ACD≌△AGB（ASA）
∴S△ACD=S△AGB，AG=AC
∴S△ACD+S△ABC=S△AGB+S△ABC
∴S四边形ABCD=S△ACG=.
如何选择合适的话费套餐
素材1
中国移动A套餐：月租费为58元/月，套餐内每月可拨打国内电话150分钟，超出套餐部分拨打国内电话0.19元/分钟.
素材2
中国移动B套餐：月租费为88元/月，套餐内每月可拨打国内电话350分钟，超出套餐部分拨打国内电话0.19元/分钟.
素材3
中国移动推出的A，B两种套餐都在全国范围内接听免费，含来电显示.
套餐收费说明：如A套餐计费方法中，若拨打国内电话时长小于等于150分钟，则只收月租费58元/月；若拨打国内电话时长为180分钟，则该月计费为58+（180-150）×0.19=63.7元.
任务一
某用户选择中国移动B套餐：
若该月拨打国内电话时长为200分钟，则该用户的月缴费为 元；
若该月拨打国内电话时长为380分钟，则该用户的月缴费为 元.
任务二
若选择A套餐计费方法，设某用户一个月的拨打国内电话时长为x分钟（x>150），该月话费为y1元，则y1与x的关系式是 ；若选择B套餐计费方法，设某用户一个月的拨打国内电话时长为x分钟（x>350），该月话费为y2元，则y2与x的关系式是 .
任务三
若某用户某月拨打国内电话总时长为250分钟，你认为他应该选择上述两种套餐中的哪一种较为合算?请说明你的理由.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
D
C
B
A
D
C
B
D