2023-2024学年陕西省西安市雁塔区高新一中八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年陕西省西安市雁塔区高新一中八年级（下）期末数学试卷（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.下列方程中一定是一元二次方程的是( )
A. x2=0B. x2−2y+1=0C. ax2+bx+c=0D. 1x−5x2+6=0
2.下列条件中，能判断四边形ABCD是平行四边形的是( )
A. AB // CD，AD=BCB. ∠A=∠B，∠C=∠D
C. AB=AD，CB=CDD. AB // CD，AB=CD
3.用配方法解一元二次方程x2−6x−2=0，配方后得到的方程是( )
A. (x−3)2=2B. (x−3)2=8C. (x−3)2=11D. (x+3)2=9
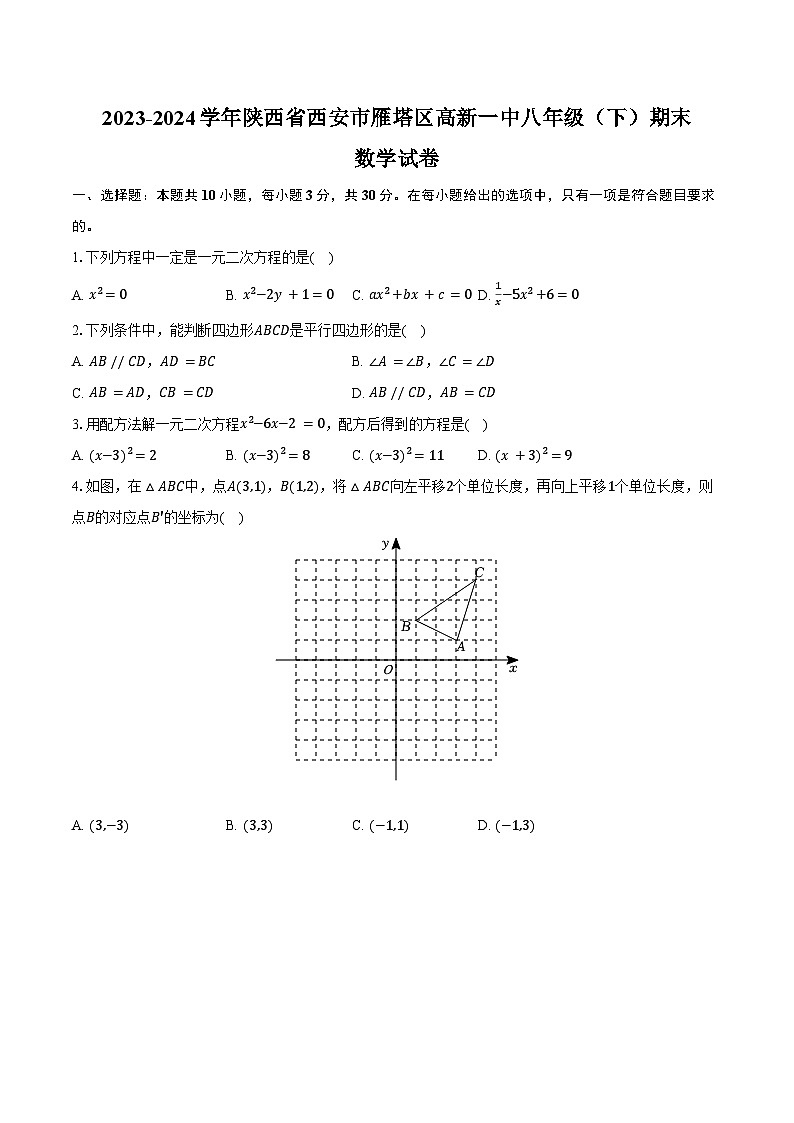
4.如图，在△ABC中，点A(3,1)，B(1,2)，将△ABC向左平移2个单位长度，再向上平移1个单位长度，则点B的对应点B′的坐标为( )
A. (3,−3)B. (3,3)C. (−1,1)D. (−1,3)
5.如图，在矩形COED中，点D的坐标是(1,3)，则CE的长是( )
A. 3B. 2 2C. 10D. 4
6.某校组织540名学生去外地参观，现有A，B两种不同型号的客车可供选择.在每辆车刚好满座的前提下，每辆B型客车比每辆A型客车多坐15人，单独选择B型客车比单独选择A型客车少租6辆.设A型客车每辆坐x人，根据题意可列方程( )
A. 540x−15−540x=6B. 540x−540x+15=6
C. 540x+15−540x=6D. 540x−540x−15=6
7.如图，在△ABC中，点F在BC上，AC=CF，CD⊥AF，垂足为D，E为AB的中点，AC=6，BC=10，则ED的长为( )
A. 2
B. 3
C. 52
D. 4
8.关于x的方程2x−1x−2=mx−2+1有增根，则m的值是( )
A. 0B. 2或3C. 2D. 3
9.如图，已知一次函数y=kx+b的图象经过点A(−1,2)和点B(−2,0)，一次函数y=mx的图象经过点A，则关于x的不等式组0A. −2B. −1C. x<−1
D. x>−1
10.如图，在△ABC中，∠B=45°，∠C=60°，BC=6，点P为AC边上一动点，PE⊥AB于点E，PF⊥BC于点F，连接EF，则EF的最小值为( )
A. 3 6
B. 32 5
C. 32 6
D. 32
二、填空题：本题共7小题，每小题3分，共21分。
11.因式分解：9x−4x3= ______．
12.一元二次方程3x2=27的解为：______．
13.八边形的内角和是______，它共有条______对角线．
14.如图，五边形ABCDE中，∠A=125°，则∠1+∠2+∠3+∠4的度数是______．
15.已知a、b、c为△ABC的三边，且满足a2c2−b2c2=a4−b4，则△ABC为______三角形．
16.如图，点P是矩形ABCD的对角线AC上一点，过点P作EF/​/BC，分别交AB、CD于E、F，连接PB、PD.若AE=2，PF=5.则图中阴影部分的面积为______．
17.如图，在平行四边形ABCD中，∠B=30°，AB=2 3，将△ABC沿AC翻折至△AB′C，连接B′D.当BC长为______时，△AB′D是直角三角形．
三、解答题：本题共9小题，共69分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题4分)
解不等式组：2x+1>−13x−1219.(本小题12分)
解方程：
(1)2x(x+3)=3(x+3)；
(2)(x−3)(2x+5)=−14；
(3)x+1x−1−4x2−1=1．
20.(本小题5分)
先化简再求值：x−3x2+6x+9÷(1−6x+3)，其中x=1．
21.(本小题6分)
如图，AB/​/CD，连接BC，请用尺规作图法，分别在AB，CD上求作E，F，连接CE，BF，使得四边形CEBF是菱形.(保留作图痕迹，不写作法)
22.(本小题6分)
如图，在△ABC中，BE平分∠ABC，DE/​/BC，∠EFC=2∠ABE．
求证：四边形DBFE是菱形．
23.(本小题8分)
正所谓“道路通达，百业兴旺”，某村决定对村里的部分道路进行整改，将工程交由甲、乙两个工程队来完成.已知甲工程队每天比乙工程队多修0.4km，如果甲工程队修6.4km所用的天数是乙工程队修9.6km所用天数的一半．
(1)求甲，乙两个工程队每天各修路多少km？
(2)现计划再修建长度为24km的道路，由甲、乙两个工程队来完成.若甲队每天所需费用为2.4万元，乙队每天所需费用为1.5万元，求在总费用不超过33.6万元的情况下，至少安排乙工程队施工多少天？
24.(本小题8分)
如图，△ABC中，AB=AC，AD是∠BAC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．
(1)求证：四边形AEBD是矩形；
(2)当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．
25.(本小题8分)
如图，在平面直角坐标系中，直线l1：y=12x+1与x轴交于点B，直线l2与直线l1、x轴分别交于点A(1,32)、点C(4,0)．
(1)求直线l2的解析式；
(2)若点D和点E分别是直线l2和y轴上的动点，是否存在点D、E，使得以点A、B、D、E为顶点、AB为一边的四边形是平行四边形？若存在，请求出点D的坐标；若不存在，请说明理由．
26.(本小题12分)
在菱形ABCD中，∠ABC=60°，P是直线BD上一动点，以AP为边向右侧作等边△APE(A,P,E按逆时针排列)，点E的位置随点P的位置变化而变化．
(1)如图1，当点P在线段BD上，且点E在菱形ABCD内部或边上时，连接CE，则BP与CE的数量关系是______，BC与CE的位置关系是______；
(2)如图2，当点P在线段BD上，且点E在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；
(3)当点P在直线BD上时，其他条件不变，连接BE.若AB=2 3，BE=2 19，请直接写出△APE的面积．
参考答案
1.A
2.D
3.C
4.D
5.C
6.B
7.A
8.D
9.A
10.C
11.x(3+2x)(3−2x)
12.x1=3，x2=−3
13.1080° 20
14.305°
15.等腰或直角或等腰直角
16.10
17.6或4或3
18.解：2x+1>−1①3x−12解不等式①得：x>−1，
解不等式②得：x<3，
∴不等式组的解集为−119.解：(1)原方程可化为2x(x+3)−3(x+3)=0，
即(x+3)(2x−3)=0，
∴x+3=0或2x−3=0，
∴x1=−3，x2=32；
(2)原方程可化为2x2+5x−6x−15=−14，
即2x2−x−1=0，
(x−1)(2x+1)=0，
x−1=0或2x+1=0，
∴x1=1，x2=−12；
(3)x+1x−1−4x2−1=1，
去分母得：(x+1)2−4=x2−1，
整理得：2x=2，
解得：x=1，
检验：当x=1时，(x+1)(x−1)=0，
∴x=1是原方程的增根，
∴原方程无解．
20.解：x−3x2+6x+9÷(1−6x+3)，
=x−3(x+3)2÷x+3−6x+3
=x−3(x+3)2⋅x+3x−3
=1x+3，
当x=1时，原式=11+3=14．
21.解：如图，点E、F为所作．

22.证明：∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠EFC=2∠ABE=∠ABC，
∴EF//AB，
∴四边形DBFE是平行四边形，
∵DE/​/BC，
∴∠DEB=∠CBE，
∴∠ABE=∠DEB，
∴DE=DB，
∴四边形DBFE是菱形．
23.解：(1)设乙工程队每天修路x km，则甲工程队每天修路(x+0.4)km，
根据题意得：6.4x+0.4=9.6x×12，
解得：x=1.2，
经检验，x=1.2是所列方程的解，且符合题意，
∴x+0.4=1.2+0.4=1.6．
答：甲工程队每天修路1.6km，乙工程队每天修路1.2km；
(2)设安排乙工程队施工m天，则安排甲工程队施工24−1.2m1.6天，
根据题意得：2.4×24−1.2m1.6+1.5m≤33.6，
解得：m≥8，
∴m的最小值为8．
答：至少安排乙工程队施工8天．
24.(1)证明：∵点O为AB的中点，连接DO并延长到点E，使OE=OD，
∴四边形AEBD是平行四边形，
∵AB=AC，AD是∠BAC的角平分线，
∴AD⊥BC，
∴∠ADB=90°，
∴平行四边形AEBD是矩形；
(2)当∠BAC=90°时，
理由：∵∠BAC=90°，AB=AC，AD是∠BAC的角平分线，
∴AD=BD=CD，
∵由(1)得四边形AEBD是矩形，
∴矩形AEBD是正方形．
25.解：(1)设直线l2的解析式为y=kx+b，
∵直线l2与直线l1、x轴分别交于点A(1,32)、点C(4,0)，
∴k+b=324k+b=0，解得k=−12b=2，
直线l2的解析式为y=−12x+2；
(2)存在，
∵直线l1：y=12x+1与x轴交于点B，
∴B(−2,0)，
设D(t,−12t+2)，E(0,m)，
①当AB为平行四边形的对角线时，

∵A(1,32)，B(−2,0)，
∴−2+1=t+032+0=−12t+2+m，
解得t=−1m=−1，
∴D(−1,52)；
②当AD为平行四边形对角线时，

∵A(1,32)，B(−2,0)，
∴−2+0=1+tm+0=−12t+2+32，
解得t=−3m=5，
∴D(−3,72)；
③当AE为平行四边形的对角线时，

∵A(1,32)，B(−2,0)，
∴0+1=−2+tm+32=−12t+2+0，
解得t=3m=−1，
∴D(3,12)；
综上所述：存在，D点坐标为(−1,52)或(−3,72)或(3,12).
26.BP=CE BP⊥CE