

数学九年级上册26.4 解直角三角形的应用课文课件ppt
展开1. 了解方位角的概念,能根据题意辨识对应的方位角.2. 结合具体问题情境,会画方位角示意图.3. 学会将实际问题转化为解直角三角形问题,提高分析和解决问题的能力,提高学习数学的兴趣和应用意识.
1.如图,以屏幕中的点O为基准,认识一下方向
“上北下南,左西右东”
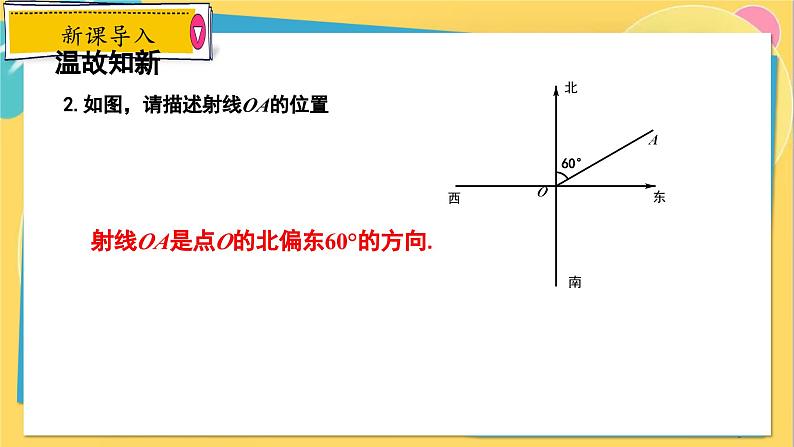
2.如图,请描述射线OA的位置
射线OA是点O的北偏东60°的方向.
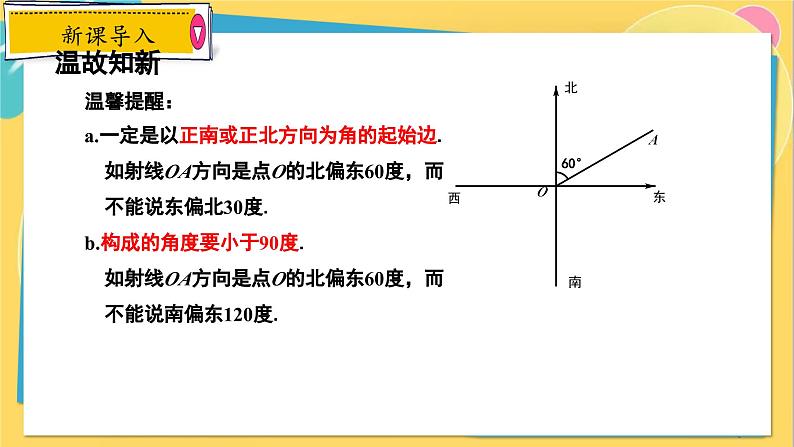
温馨提醒:a.一定是以正南或正北方向为角的起始边. 如射线OA方向是点O的北偏东60度,而 不能说东偏北30度.b.构成的角度要小于90度. 如射线OA方向是点O的北偏东60度,而 不能说南偏东120度.
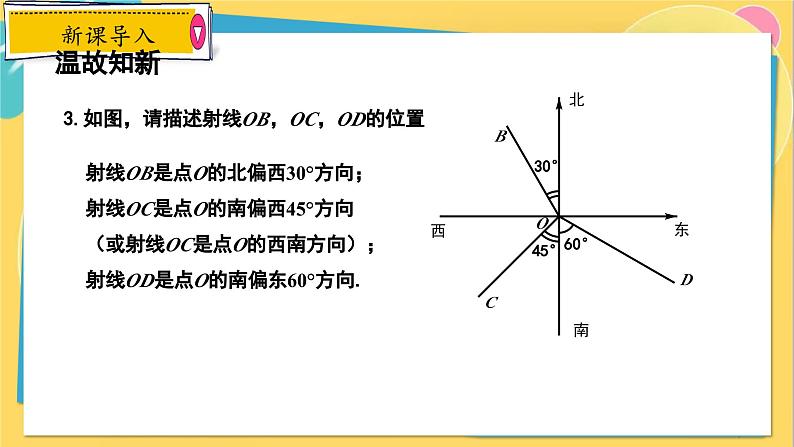
3.如图,请描述射线OB,OC,OD的位置
射线OB是点O的北偏西30°方向;射线OC是点O的南偏西45°方向(或射线OC是点O的西南方向);射线OD是点O的南偏东60°方向.
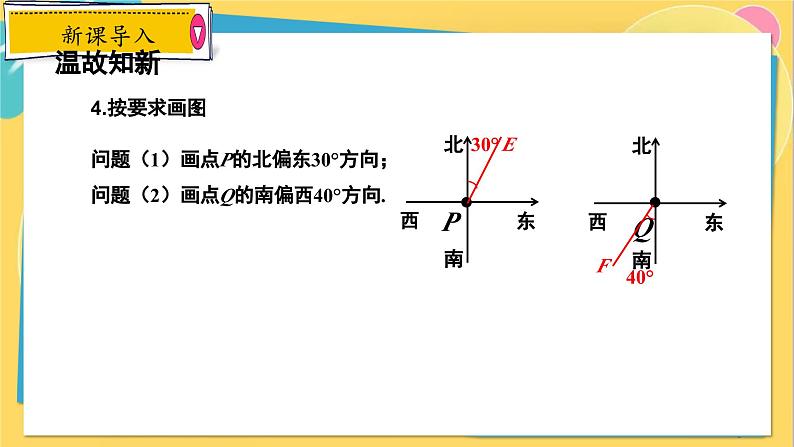
问题(1)画点P的北偏东30°方向;问题(2)画点Q的南偏西40°方向.
(1)根据题意找好基准点.(2)以基准点为标准画出正南或正北的方向线.(3)构成的角度小于90°.
两个不同点的方位角问题
如图所示,一艘渔船以30海里/时的速度由西向东航行. 在A处看见小岛C在船北偏东60°的方向上.40 min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上. 已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区. 如果这艘渔船继续向东航行,有没有进入危险区的可能?
Rt△BCD中,∠CBD=60°;Rt△ACD中,∠CAD=30°
(1)如何判断有没有进入危险区的可能?
点C到直线AB的距离与10海里比较大小
(2)要求点C到直线AB的距离,需要作什么辅助线?
过点C作CD⊥AB,交AB的延长线于点D
(3)要求CD的长,CD在哪个直角三角形中?
Rt△BCD和Rt△ACD中
(4)Rt△BCD和Rt△ACD中,有什么已知条件?
(5)设CD=x,则直角三角形中的边长能否用x表示?
(6)题目中的等量关系是什么?你能列方程求解吗?
解:如图所示,过点C作CD⊥AB,交AB的延长线于点D,则∠CBD=60°,
在Rt△BCD中,tan∠CBD=tan 60°= .
在Rt△ACD中,∠CAD=30°,所以
所以这艘渔船继续向东航行,不会进入危险区.
如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.(1)在图中画出点B,并求出B处与灯塔P的距 离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置 (参考数据:sin 53°≈0.80, cs 53°≈0.60, tan 53°≈1.33, ≈1.41).
(1)点B的位置如图所示. 根据题意,得∠A=53°,∠B=45°. 在Rt△APC中, ∵sin A= ∴PC=PA·sin 53° ≈100×0.80 =80(n mile).
(2)方法一:在Rt△BPC中,∵sin B=∴方法二:在Rt△BPC中,∵∠B=∠BPC=45°,∴PC=BC.∴PB= 即B处与灯塔P的距离大约是113 n mile.答:灯塔P位于B处的西北(或北偏西45°)方向,距离B处 大约113 n mile.
如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离250( +1)m.已知在以油库C为中心,半径为200 m的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
如图,过点C作CD⊥AB于D,则BD=CD,AD=∵BD+AD=AB=250( +1)(m), 即 CD+CD=250( +1),∴CD=250 m, 250 m>200 m,故在此路段修建铁路,油库C是不会受到影响的.
同一点的两个方位角问题
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为30 n mile/h,在此航行过程中,问该渔船从B处开始航行多长时间,离观测点A的距离最近?(计算结果用根号表示,不取近似值)
如图,过点A作AP⊥BC,垂足为P,设AP=x n mile.在Rt△APC中,∵∠APC=90°,∠PAC=30°,∴tan∠PAC=∴CP=AP·tan∠PAC= x n mile. 在Rt△APB中,∵∠APB=90°,∠PAB=45°,∴BP=AP=x n mile.
∵PC+BP=BC=30× =15(n mile),∴ x+x=15.解得x=∴PB= n mile.∴航行时间为 即该渔船从B处开始航行 离观测点A 的距离最近.
如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了 m到达B地,然后再沿北偏西30°方向走了500 m到达目的地C .(1)A、C两地间的距离;(2)确定目的地C在营地A的什么方向上?
实际问题转化为数学问题:(1)求AC的长;(2)求射线AC的方向.
数学问题转化为解直角三角形问题:
解:根据题意,∠FAB=60°,∠DBC=30°, ∵AF∥BE,∴ ∠ABE=∠FAB=60°. ∴ ∠ABC=90°.
根据勾股定理可得 AC=1000(m).
∴A、C两地间的距离为1000m,目的地C在营地A的北偏东30°的方向上.
解决与方位角有关的实际问题时,必须先在每个位置 中心建立方向标,然后根据方位角标出图中已知角的 度数,最后在某个直角三角形内利用锐角三角函数解 决问题.
为了美化环境,提高民众的生活质量,市政府在三角形花园ABC边上修建一个四边形人工湖泊ABDE,并沿湖泊修建了人行步道.如图,点C在点A的正东方向170米处,点E在点A的正北方向,点B,D都在点C的正北方向, BD长为100米,点B在点A的北偏东30°方向,点D在点E的北偏东58°方向.
(1)步道DE的长度为________米(结果精确到个位);
九年级上册26.4 解直角三角形的应用背景图ppt课件: 这是一份九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">26.4 解直角三角形的应用背景图ppt课件</a>,共30页。PPT课件主要包含了知识回顾,知识点,感悟新知等内容,欢迎下载使用。
冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt: 这是一份冀教版九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt</a>,共34页。PPT课件主要包含了与测量有关的术语,巩固概念,知识点,坡度的应用,实际问题,数学模型,感悟新知,坡角的应用等内容,欢迎下载使用。
冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用课堂教学ppt课件: 这是一份冀教版九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">第26章 解直角三角形26.4 解直角三角形的应用课堂教学ppt课件</a>,共26页。PPT课件主要包含了知识点,感悟新知,课堂小结等内容,欢迎下载使用。













