

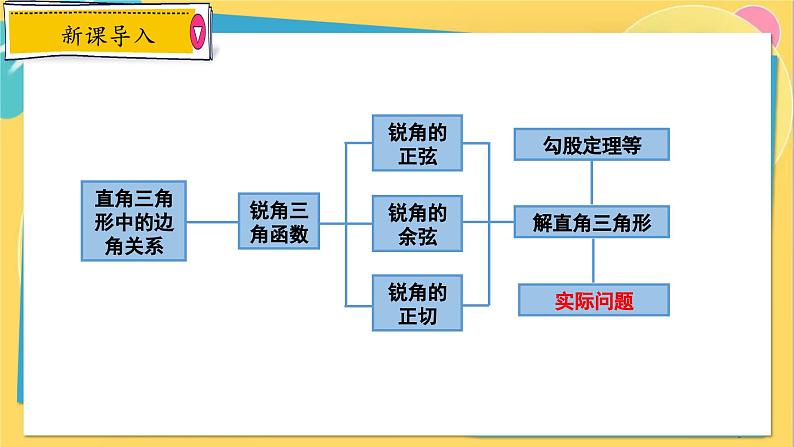


冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用课堂教学ppt课件
展开1. 了解仰角、俯角等与测量有关的的术语,弄清它们的意义.2. 学会用解直角三角形的有关知识去解决某些简单的与仰角、俯角有关的实际问题.3.学会将实际问题抽象成数学问题,从而进一步把形和数结合起来,提高分析和解决问题的能力.
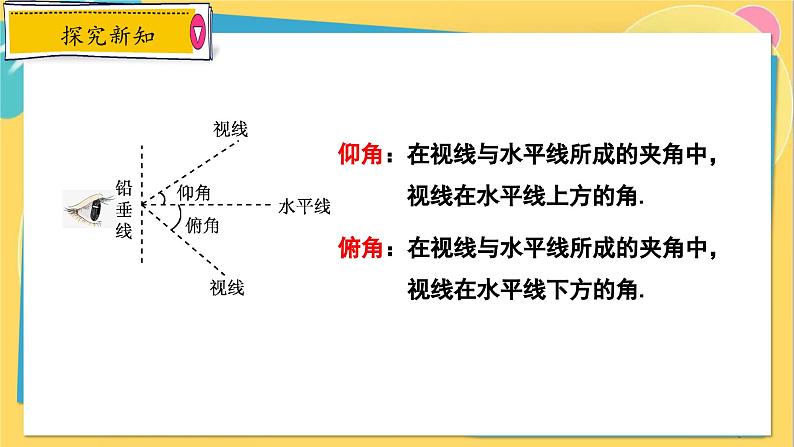
平时我们观察物体时,我们的视线相对于水平线来说可能有几种情况?三种:重叠、向上、向下
仰角:在视线与水平线所成的夹角中, 视线在水平线上方的角.
俯角:在视线与水平线所成的夹角中, 视线在水平线下方的角.
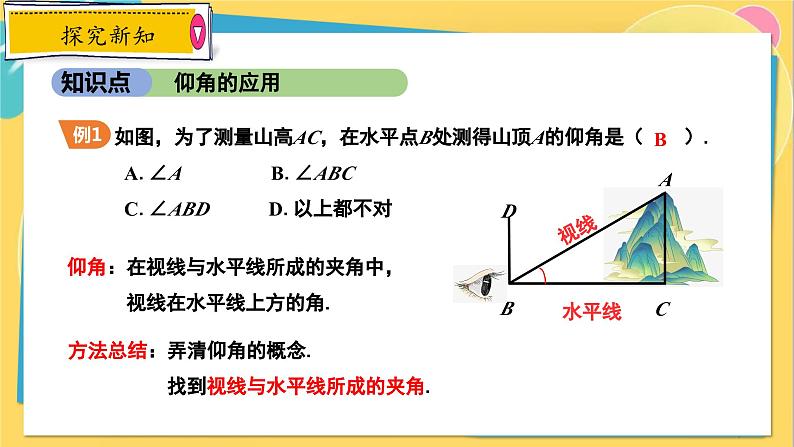
如图,为了测量山高AC,在水平点B处测得山顶A的仰角是( ). A.∠A B.∠ABC C.∠ABD D.以上都不对
方法总结:弄清仰角的概念. 找到视线与水平线所成的夹角.
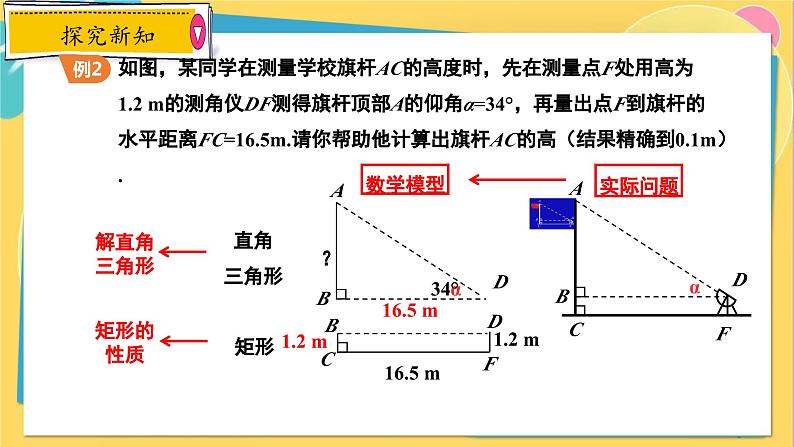
如图,某同学在测量学校旗杆AC的高度时,先在测量点F处用高为1.2 m的测角仪DF测得旗杆顶部A的仰角α=34°,再量出点F到旗杆的水平距离FC=16.5m.请你帮助他计算出旗杆AC的高(结果精确到0.1m).
设水平线DB与旗杆AC交于点B,由题意得四边形BCFD为矩形,
∴BD=CF=16.5,BC=DF=1.2.
在Rt△ABD中,∠ABD=90°,∠ADB=34°
∴AC=AB+BC≈11.13+1.2=12.33≈12.3 (m).
答:旗杆的高约为12.3 m.
1.将实际问题转化为数学问题 (画出平面图形).
3.得到数学问题的答案.
(已知一边一角求另一边)
如图,某班学生利用周末到白塔山去参观“晏阳 初博物馆”.下面是两位同学的一段对话: 甲:我站在N处看塔顶,仰角为60°. 乙:我站在M处看塔顶,仰角为30°. 甲:我们的身高都是1.5 m. 乙:我们和塔在一条直线上,且我们相距20 m. 请你根据两位同学的对话,计算白塔的高度.(结 果精确到1 m).
由题意知∠CAB=30°,∠CBD=60°,AB=20 m, AM=BN=DP=1.5 m. 在△ABC中,∠CBD=∠ACB+∠CAB,∴∠ACB=60°-30°=30°.∴∠ACB=∠CAB.∴BC=AB=20 m. 在Rt△CBD中,BC=20 m,∠CBD=60°, sin ∠CBD=
∴CD=BC·sin ∠CBD=20sin 60°=20× (m).∴CP=CD+DP=10 +1.5≈19(m).答:白塔的高度约为19 m.
从不同位置看同一点测高度时,往往用高度来表示这两个不同位置到被测物底部的距离.然后利用两次测量的不同位置之间的距离来解决问题.
小明在热气球A上看到正前方横跨河流两岸的大桥 BC,并测得B,C两点的俯角分别为45°,35°,如图 所示.已知大桥BC与地面在同一水平面上,其长度为100 m.请求出热气球离地面 的高度.(结果保留整数. 参考数据:sin 35°≈0.574, cs 35°≈0.819, tan 35°≈0.700)
过点A作AD⊥BC于点D,热气球离地面的高度即为AD的长.利用BC长度转化为CD-BD=BC,由辅助线构造出Rt△ABD,Rt△ACD,利用解直角三角形求解.如图,作AD⊥BC于点D.由题意得∠ABD=45°,∠ACD=35°,BC=100 m.设AD=x m,则BD=AD=x m,CD= m.∵BC=CD-BD,∴ -x=100.∴x≈233.答:热气球离地面的高度约为233 m.
从同一点看不同的位置,有两个视角,不同位置之间有距离,作垂线将两个视角都放在直角三角形中,利用不同位置之间的距离列方程来解决问题.
如图所示,小明在距旗杆4.5 m的点D处,仰视旗杆顶端A,仰角(∠AOC)为50°;俯视旗杆底部B,俯角(∠BOC)为18°. 求旗杆的高. (结果精确到0.1 m)
如图,作OC⊥AB于点C. 由题意得∠AOC=50°,∠BOC=18°,OC=BD=4.5 m. ∴AB=AC+CB=5.4+1.5=6.9 (m).答:旗杆高度约为6.9 m.
解答含有仰角、俯角问题的方法:(1)仰角和俯角是视线相对于水平线而言的,不同位置的仰 角和俯角是不同的,可巧记为“上仰下俯”.在测量物 体的高度时,要善于将实际问题抽象为数学问题.(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯 角)和另一边,利用解直角三角形的知识就可以求出物 体的高度.(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实 际问题中的数量关系归结到直角三角形中来求解.
1.[2023·泰安]在一次综合实践活动中,某学校数学兴趣小组对一电视发射塔的高度进行了测量.如图,在塔前C处,测得该塔顶端B的仰角为50°,后退60 m(CD= 60 m)到D处有一平台,在高2 m(DE=2 m)的平台上的E处,测得B的仰角为26.6°,则该电视发射塔的高度AB为________m.(精确到1 m,参考数据:tan 50°≈1.2,tan 26.6°≈0.5)
【点拨】如图,过点E作EF⊥AB,垂足为点F,由题意得AF=DE=2 m,EF=AD,BA⊥DA,设AC=x m,∵CD=60 m,∴EF=AD=AC+CD=(x+60)m.
2.[2023·孝感]综合实践课上,航模小组用航拍无人机进行测高实践.如图,无人机从地面CD的中点A处竖直上升30米到达B处,测得博雅楼顶部E的俯角为45°,尚美楼顶部F的俯角为30°,已知博雅楼高度CE为15米,则尚美楼高度DF为________米(结果保留根号).
【点拨】如图,过点E作EM⊥过点B的水平线于点M,过点F作FN⊥过点B的水平线于点N,易知BN=AD,BM=AC,CM=DN=AB=30米.∵CE=15米,∴EM=15米.在Rt△EBM中,∠EBM=45°,∴BM=EM=15米.
九年级上册26.4 解直角三角形的应用背景图ppt课件: 这是一份九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">26.4 解直角三角形的应用背景图ppt课件</a>,共30页。PPT课件主要包含了知识回顾,知识点,感悟新知等内容,欢迎下载使用。
冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt: 这是一份冀教版九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">第26章 解直角三角形26.4 解直角三角形的应用图片课件ppt</a>,共34页。PPT课件主要包含了与测量有关的术语,巩固概念,知识点,坡度的应用,实际问题,数学模型,感悟新知,坡角的应用等内容,欢迎下载使用。
数学九年级上册26.4 解直角三角形的应用课文课件ppt: 这是一份数学九年级上册<a href="/sx/tb_c107219_t3/?tag_id=26" target="_blank">26.4 解直角三角形的应用课文课件ppt</a>,共30页。PPT课件主要包含了温故知新,知识点,课堂小结等内容,欢迎下载使用。













