初中数学冀教版九年级上册25.6 相似三角形的应用课前预习ppt课件

这是一份初中数学冀教版九年级上册25.6 相似三角形的应用课前预习ppt课件，共17页。PPT课件主要包含了小明是怎么做的呢，知识点等内容，欢迎下载使用。

1.进一步巩固相似三角形的知识，能够运用三角形相似的知识解决不能直接测量的物体的高度和距离等一些实际问题；2.通过把实际问题转化成有关相似三角形的数学模型，进一步了解数学建模的思想，培养抽象、运算、推理、作图的能力；3.体会数学在生活中的作用，提高运用数学方法解决问题的能力，增强学习数学的兴趣．
小明和妈妈散步来到小河的南岸
妈妈：这条小河有多宽呢？可惜咱们不能到河的对岸量一量.
小明：我可以用刚学的相似三角形的知识测出来.
1.如图，在一条小河的北岸A处有一古塔，南岸C处有一观景台.为求古塔和观景台之间的距离，请你设计测量方案，并给出计算结果.
利用相似三角形测量物体的宽度
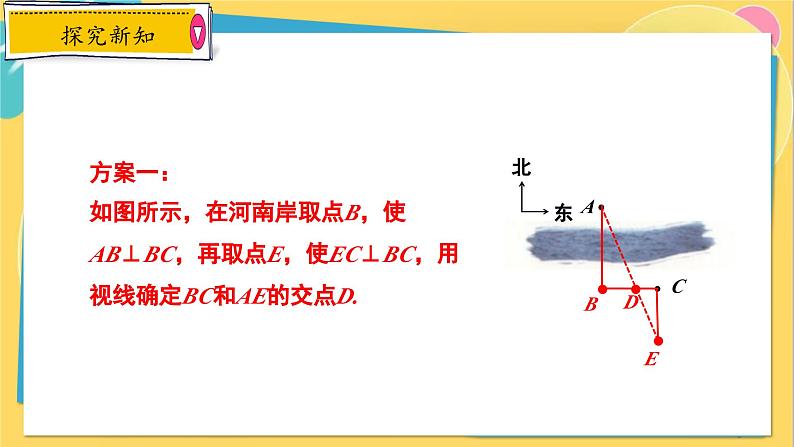
方案一：如图所示，在河南岸取点B，使AB⊥BC，再取点E，使EC⊥BC，用视线确定BC和AE的交点D.
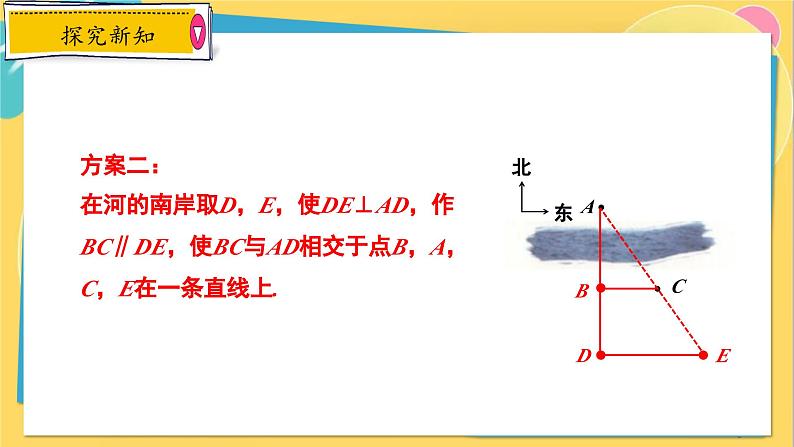
方案二：在河的南岸取D，E，使DE⊥AD，作BC∥DE，使BC与AD相交于点B，A，C，E在一条直线上.
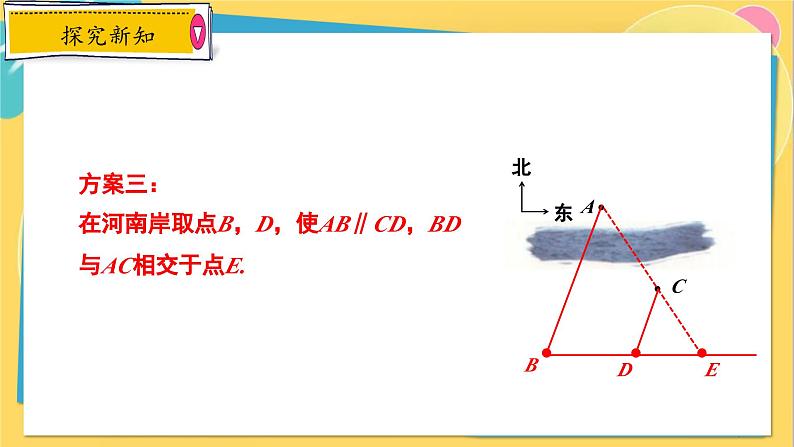
方案三：在河南岸取点B，D，使AB∥CD，BD与AC相交于点E.
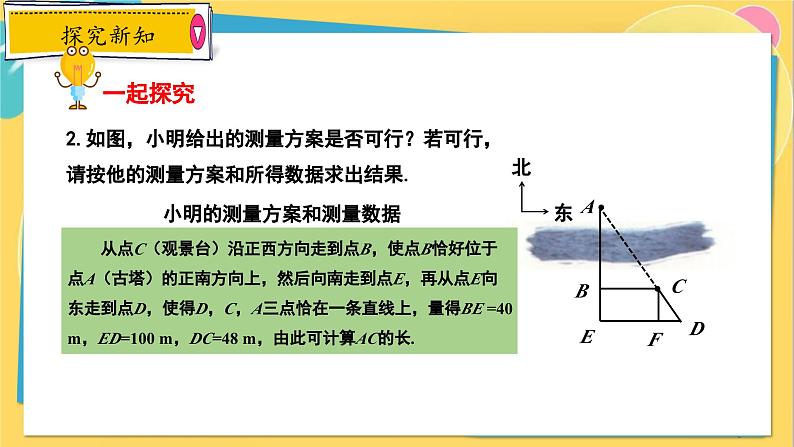
2.如图，小明给出的测量方案是否可行？若可行，请按他的测量方案和所得数据求出结果.
解：小明给出的方案可行.由题意可知，BC⊥AE，AE⊥DE，CF⊥DE，则四边形BCFE为矩形.∴CF∥AE，CF=BE=40 m，在Rt△DCF中，∵DC=48 m，CF=40 m，∴DF=∵ CF∥AE，∴△DCF∽△DAE，∴AD= ，∴AC=AD－DC= －48.
测量如河宽等不易直接测量的物体的宽度，常构造相似三角形求解.
如图所示，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上. 若测得BE=20 m，EC=10 m，CD=20 m，则河的宽度AB等于(　　)A.60 m B.40 m C.30 m D.20 m
如图所示，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12 m，由此他就知道了A，B间的距离. 有关他这次探究活动的描述错误的是(　　)A.AB=24 m B.MN∥ABC.△CMN∽△CAB D.CM∶MA=1∶2
如图所示，△ABC为一块铁板余料，已知BC=120 mm，高AD=80 mm，要用这块余料裁出一个正方形材料，且使正方形的一边在BC上，其余两个顶点分别在AB，AC上，这个正方形的边长应为多少毫米?
思考(1)图中△AHG与△ABC是否相似?为什么?
(2)相似三角形的对应高之间有什么性质?
(4)你能通过设未知数，利用方程思想求解图中正方形的边长吗?
(3)图中△AHG与△ABC的高之间与正方形的边长有什么关系?
答：裁出的正方形的边长为48 mm.
如图所示，为测量被障碍物隔开的A，B两点间的距离，分别在点A，B处竖立标杆，并寻找点O，通过观测，确定点C，使点O，C，A在一条直线上. 如果测得OA的长是OC长的100倍，那么，接下来该怎样做，才能算出A，B两点间的距离?
参考方案：在OB上确定点D，使OB=100OD，连接CD，则有△OCD∽△OAB，再测量出CD的长，于是AB=100CD.这样就可以算出A，B两点间的距离.