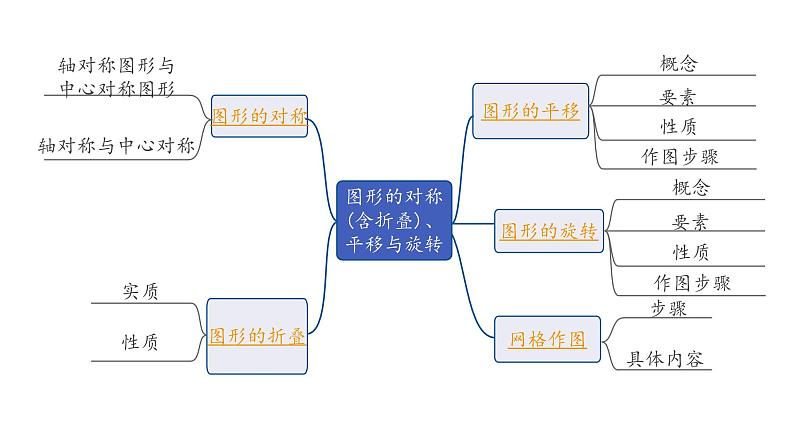
2024内蒙古中考数学一轮复习 第33课时 图形的对称(含折叠)、平移与旋转（课件）

这是一份2024内蒙古中考数学一轮复习 第33课时 图形的对称(含折叠)、平移与旋转（课件），共50页。PPT课件主要包含了考点精讲，图形的对称，图形的折叠，图形的平移，平移距离，平行或共线且相等，图形的旋转，旋转方向，网格作图，AC＝DF等内容，欢迎下载使用。

图形的对称(含折叠)、平移与旋转
【对接教材】北师：七下第五章P114～P134， 八上第三章P68～P70， 八下第三章P64～P90； 人教：七下第五章P28～P33， 七下第七章P75～P82， 八上第十三章P58～P74、P85～P88， 九上第二十三章P59～P77.
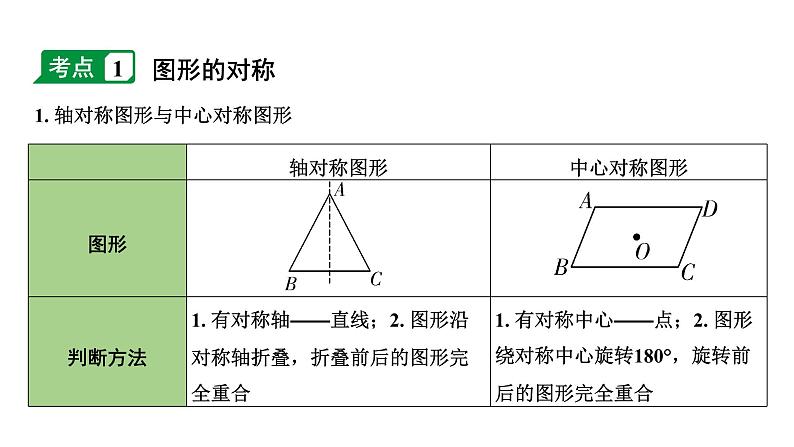
1. 轴对称图形与中心对称图形
常见的轴对称图形：等腰三角形、等边三角形、菱形、矩形、正方形、正六边形、圆等；常见的中心对称图形：平行四边形、菱形、矩形、正方形、正六边形、圆等；常见的既是轴对称图形又是中心对称图形：菱形、矩形、正方形、正六边形、圆等
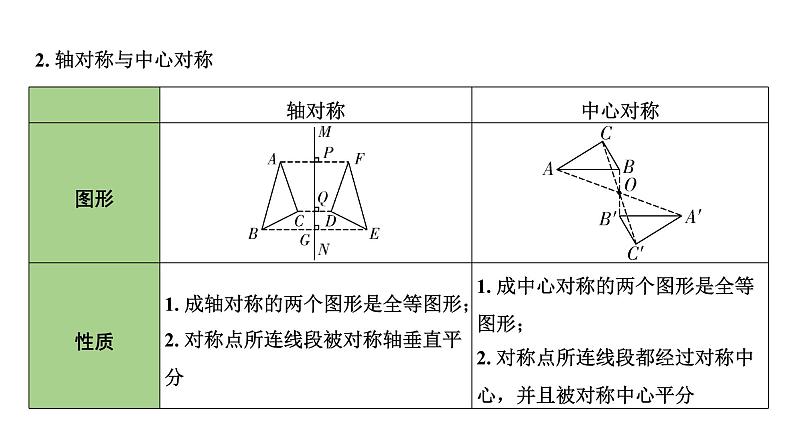
2. 轴对称与中心对称
一、与平移有关的证明与计算
(1)AC与DF的数量关系为____________，位置关系为________，与∠BAC相等的角有_____________________________；(2)AD的长为________，△ABC≌________；(3)四边形ACFD的周长为________；(4)线段AD、EF、BF之间的数量关系为_____________________．
∠EDF、∠EGC和∠AGD
(1)如图②，将△ABC沿AC方向平移得到△A′B′C′，当A′为AC的中点时．①△A′B′C′的面积为________，平移距离AA′的长度为________；
②连接A′D、B′C，判断四边形A′B′CD的形状是________________；
(2)如图③，将△ABC沿BC方向平移得到△A′B′C′，A′B′交AC于点E.①∠A′EC的度数为________；
【解法提示】∵四边形ABCD为正方形，AC为对角线，∴∠CAD＝45°，∵△ABC沿BC方向平移，∴A′B′∥CD，∴∠A′EA＝45°，∴∠A′EC＝135°.
②若两个三角形重叠部分(图中阴影)的面积为12，求平移距离AA′的长度；
②∵四边形ABCD为正方形，∴AB∥DC.由平移的性质可知AC∥A′C′，A′B′∥DC，∴阴影部分为平行四边形，∴S阴影＝A′E·A′D＝12.设AA′＝x，则A′E＝A′A＝x，A′D＝8－x，∴x(8－x)＝12，解得x1＝2，x2＝6，∴平移距离AA′的长度为2或6；
二、与旋转有关的证明与计算
例3　如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转后得到△EDC.(1)旋转角为________________________；(2)在旋转过程中与∠ACE恒相等的角为________；
(3)连接BD、AE，试判断△BDC和△ACE的形状____________________________________；(4)判断△BDC和△AEC是否相似？并说明理由．
△BDC和△ACE均为
(1)解：如解图，过点A1作A1G⊥AB交AB于点G，过点A1作A1H⊥BC交BC于点H，
(2)如图②，当点A1落在矩形的对角线AC上时，连接CD1，求证△BA1C≌△D1CA1；
(2)证明：由旋转的性质可得，A1B＝AB，∠BA1D1＝∠BAD＝∠CBA＝90°，A1D1＝AD＝BC，∴∠BA1A＝∠A1AB.又∵∠BAA1＋∠A1CB＝90°＝∠BA1A＋∠CA1D1，∴∠A1CB＝∠CA1D1.又∵CA1＝A1C，∴△BA1C≌△D1CA1；
(3)如图③，当边A1D1经过点C时，连接AA1，求AA1的长；
(3)解：如解图，过点A1作A1E⊥AB交AB于点E，A1F⊥BC交BC于点F.
(4)如图④，当点A1落在BC边上时，设点O是对角线AC的中点，点O的对应点为O1，连接CO1，求CO1的值．
(4)解：如解图，过点O1作O1M⊥BC交BC于点M，
∵将矩形ABCD绕点B顺时针旋转90°得到矩形A1BC1D1，AB＝9，BC＝15，∴BC1＝BC＝15，∠CBC1＝90°，BA1＝AB＝9，∴O1M∥BC1.
对称图形的判断(呼和浩特2考，赤峰3考)
1. (2021赤峰3题3分)下列垃圾分类标识图案，既是轴对称图形，又是中心对称图形的是(　　)
2. (2022呼和浩特1题3分)下面四幅图是我国传统文化与艺术中的几个经典图案，其中不是轴对称图形的是(　　)
3. (2023呼和浩特2题3分)甲骨文是我国的一种古代文字，下面是“北”“比”“鼎”“射”四个字的甲骨文，其中不是轴对称的是(　　)
对称图形性质的应用(包头2考，呼和浩特2021.15)
7．(2021鄂尔多斯)如图，已知正方形ABCD的边长为6，点F是正方形内一点，连接CF，DF，且∠ADF＝∠DCF，点E是AD边上一动点，连接EB，EF，则EB＋EF长度的最小值为________．
8. (2022呼和浩特10题3分)如图，把某矩形纸片ABCD沿EF，GH折叠(点E、H在AD边上，点F，G在BC边上)，使点B和点C落在AD边上同一点P处，A点的对称点为A′、D点的对称点为D′，若∠FPG＝90°，S△A′EP＝8，S△D′PH＝2，则矩形ABCD的长为(　　)
10. (2021鄂尔多斯)如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，将边BC沿CN折叠，使点B落在AB上的点B′处，再将边AC沿CM折叠，使点A落在CB′的延长线上的点A′处，两条折痕与斜边AB分别交于点N、M，则线段A′M的长为(　　)A. B. C. D.
11. (2021海南)如图，在矩形ABCD中，AB＝6, AD＝8，将此矩形折叠，使点C与点A重合，点D落在点D′处，折痕为EF，则AD′的长为______ ，DD′的长为________．
12. (2022赤峰7题3分)如图，Rt△ABC中，∠ACB＝90°，AB＝5，AC＝3，把Rt△ABC沿直线BC向右平移3个单位长度得到△A′B′C′，则四边形ABC′A′的面积是(　　)A. 15 B. 18 C. 20 D. 22
14. (2020赤峰3题3分)下列图形绕某一点旋转一定角度都能与原图形重合，其中旋转角度最小的是(　　)
15. (2023包头17题3分)如图，在△ABC中，∠CAB＝55°，∠ABC＝25°，在同一平面内，将△ABC绕点A逆时针旋转70°得到△ADE，连接EC，则tan∠DEC的值是________．
16. (2021桂林)如图，正方形OABC的边长为2，将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′，连接BC′，当点A′恰好落在线段BC′上时，线段BC′的长度是________．
(1)证明：∵△AOB和△MON都是等腰直角三角形，∠AOB＝∠MON＝90°，∴OA＝OB，OM＝ON.又∵∠AOM＝∠MON＋∠AON，∠BON＝∠AOB＋∠AON，∴∠AOM＝∠BON，∴△AOM≌△BON(SAS)，∴AM＝BN；
(2)将△MON绕点O顺时针旋转．①如图②，当点M恰好在AB边上时，求证：AM2＋BM2＝2OM2；
②当点A，M，N在同一条直线上时，若OA＝4，OM＝3，请直接写出线段AM的长．