


2024辽宁中考数学二轮专题复习 微专题 二次函数与平行四边形问题(课件)
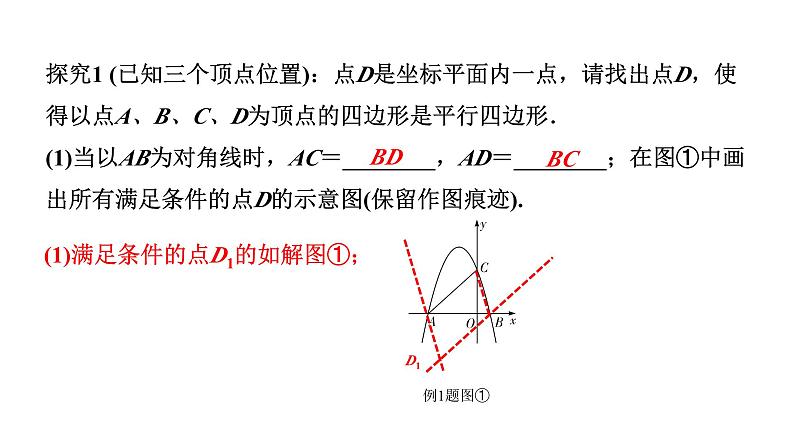
展开探究1 (已知三个顶点位置):点D是坐标平面内一点,请找出点D,使得以点A、B、C、D为顶点的四边形是平行四边形.(1)当以AB为对角线时,AC=________,AD=________;在图①中画出所有满足条件的点D的示意图(保留作图痕迹).
(1)满足条件的点D1的如解图①;
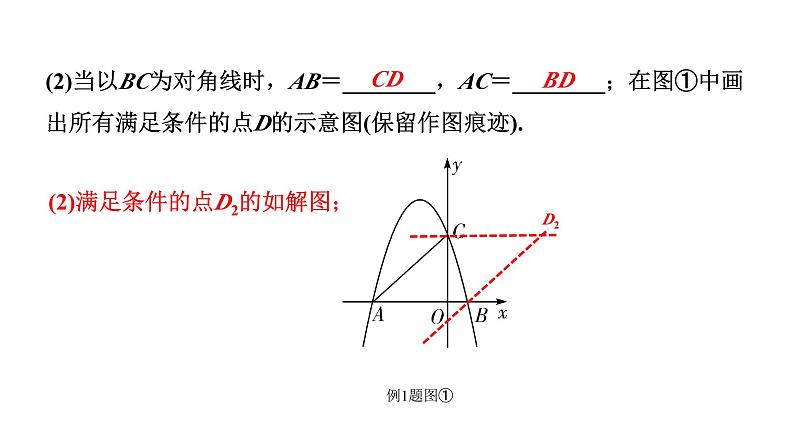
(2)当以BC为对角线时,AB=________,AC=________;在图①中画出所有满足条件的点D的示意图(保留作图痕迹).
(2)满足条件的点D2的如解图;
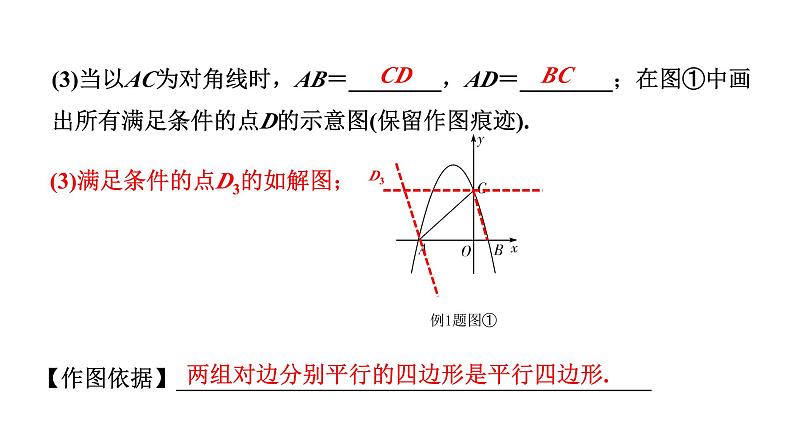
(3)当以AC为对角线时,AB=________,AD=________;在图①中画出所有满足条件的点D的示意图(保留作图痕迹).
(3)满足条件的点D3的如解图;
两组对边分别平行的四边形是平行四边形.
【作图依据】_________________________________________
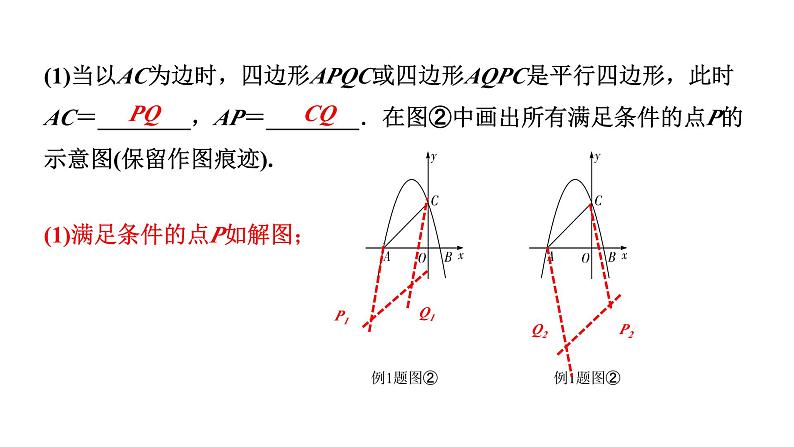
探究2(已知两个顶点位置,其余两点在函数图象上):点P是抛物线上一点,点Q是抛物线对称轴上一点,请找出点P、Q,使得以点A、C、P、Q为顶点的四边形是平行四边形.
(1)当以AC为边时,四边形APQC或四边形AQPC是平行四边形,此时AC=________,AP=________.在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
(1)满足条件的点P如解图;
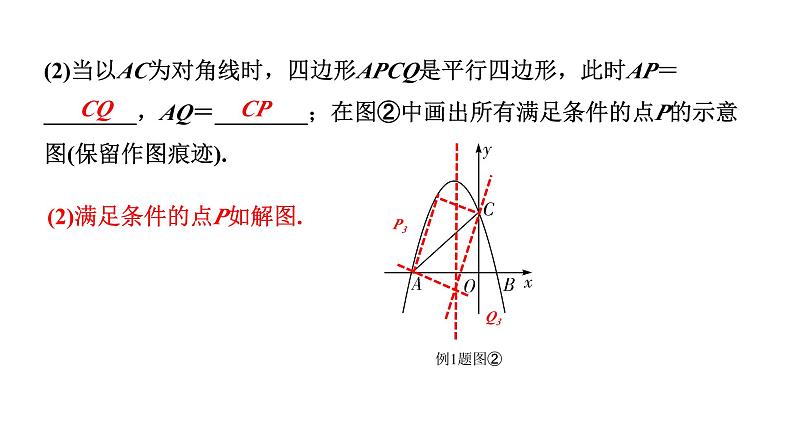
(2)当以AC为对角线时,四边形APCQ是平行四边形,此时AP=________,AQ=________;在图②中画出所有满足条件的点P的示意图(保留作图痕迹).
(2)满足条件的点P如解图.
【方法总结】二次函数中平行四边形的存在性一般要分情况讨论:常以已知线段为_______或______讨论;以探究1为例,已知AB为对角线时,作图方法为:_______________________________,所找点即为__________________的交点;若已知AB为边时,作图方法为:__________________________________________________________________,所找点即为______________________的交点.
分别过点A、C作BC,AC的平行线
分别过点A、C作BC,AB的平行线,或分别过点B、C作AC、AB的平行线
(1)求抛物线的表达式;
【思维教练】点A、B、C为定点,要使以A、B、C、P为顶点的四边形是平行四边形,则需分当AC为边或对角线时进行讨论.
(2)坐标平面内是否存在点P,使得以A、B、C、P为顶点的四边形是平行四边形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
(2)存在,点P在坐标为(4,5)或(-6,-5)或(-4,5);
【解法提示】如解图①,当AC为边时,四边形ABPC为平行四边形,则CP=AB=4,此时点P的坐标为(4,5);四边形APBC为平行四边形,则AP=BC,|xP|=AO +OB =6,yp=-yc=-5,此时点P的坐标为(-6,-5);当AC为对角线时,四边形ABCP为平行四边形,CP=AB=4,此时点P的坐标为(-4,5).综上可知,点P的坐标为(4,5)或(-6,-5)或(-4,5).
【思维教练】由GH∥x轴,AB在x轴上.可知AB∥GH,从而只需GH=AB即可得到以A、B、G、H为顶点的四边形是平行四边形.
(3)设点 G是抛物线上一点,过点 G作 GH∥x轴交对称轴 l于点 H,是否存在点 G,使得以 A、B、G、H为顶点的四边形是平行四边形,若存在,求出点 G的坐标;若不存在,请说明理由;
当g=1时,g2+6g+5=12,此时点G的坐标为G1(1,12);当g=-7时,g2+6g+5=12,此时点G的坐标为G2(-7,12).综上所述,满足条件的点G的坐标为(1,12)或(-7,12);
(4)设点 K是抛物线上一点,过 K作 KJ∥y轴,交直线 AC于点 J,是否存在点 K,使得以 M、E、K、J为顶点的四边形是平行四边形,若存在,求出点 K的坐标;若不存在,请说明理由;
【思维教练】根据点K、J分别为抛物线和直线AC上的点,设出点K、J坐标,由KJ∥ME,从而只需KJ=ME即可得到平行四边形,再根据K、J点坐标及其相对位置,求出点K坐标.
(4)存在;如解图③,设点K的坐标为(e,e2+6e+5),
∵KJ∥y轴,交直线AC于点J,易得直线AC的解析式为y=x+5,∴设点J的坐标为(e,e+5),∵M(-3,-4),E(-3,2),∴ME=6,∵ME∥y轴,KJ∥y轴,∴KJ∥ME,∴要使得以M、E、K、J为顶点的四边形为平行四边形,则KJ=ME=6,
①当点K在点J的下方时,KJ=(e+5)-(e2+6e+5)=-e2-5e,则-e2-5e=6,解得e1=-2,e2=-3(舍去),则K1(-2,-3);②当点K在点J的上方时,KJ=(e2+6e+5)-(e+5)=e2+5e,则e2+5e=6,解得e3=-6,e4=1,则K2(-6,5),K3(1,12),综上所述,满足条件的点K的坐标为(-2,-3)或(-6,5)或(1,12);
(5)设点 N是抛物线上一点,点Q是x轴上一点,是否存在点N,使得以A、E、N、Q为顶点的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
【思维教练】由AE为定边,可分AE为平行四边形一边及AE为平行四边形对角线两种情况分别确定点N.
①如解图④,当AE为平行四边形的一条边时,QN∥AE,且NQ=AE,则∠NQT=∠EAD,∵NT⊥x轴,ED⊥x轴,∴∠NTQ=∠EDA=90°,∴△QNT≌△AED,又∵AC,DM相交于点E,∴E(-3,2),∴NT=ED=2,
(5)存在;过点N作NT⊥x轴,交x轴于点T,
1. 如图,在平面直角坐标系中,抛物线y= x2+bx+c经过点A(-4,0),点M为抛物线的顶点,点B在y轴上,且OA=OB,直线AB与抛物线在第一象限交于点C(2,6).
(1)求抛物线的解析式及顶点M的坐标;
(2)求直线AB的函数解析式及sin∠ABO的值;
(2)∵A(-4,0),∴OA=4,∵OA=OB,∴OB=4,B(0,4),
(3)连接OC,若过点O的直线交线段AC于点P,将三角形AOC的面积分成1∶2的两部分,请求出点P的坐标;
(3)过点O的直线交线段AC于点P,将三角形AOC的面积分成1∶2的两部分,过P作PQ⊥x轴于点Q,过点C作CH⊥x轴于点H,分两种情况:
①当S△AOP∶S△COP=1∶2时,如解图①∵S△AOP∶S△COP=1∶2,∴S△AOP∶S△AOC=1∶3,∴PQ∶CH=1∶3,而C(2,6),即CH=6,∴PQ=2,即yP=2,在y=x+4中,令y=2得2=x+4,∴x=-2,∴P(-2,2);
∵S△COP∶S△AOP=1∶2,∴S△AOP∶S△AOC=2∶3,∴PQ∶CH=2∶3,
②当S△COP∶S△AOP=1∶2时,如解图,过点C作CH⊥x轴于点H.
∵CH=6,∴PQ=4,即yP=4,在y=x+4中,令y=4得4=x+4,∴x=0,∴P(0,4);综上所述,过点O的直线交线段AC于点P,将三角形AOC的面积分成1∶2的两部分,则点P坐标为(-2,2)或(0,4);
(4)在坐标平面内是否存在点N,使以点A、O、C、N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【解法提示】设N(m,n),分三种情况:
①以AN、CO为对角线,此时AN中点与CO中点重合,∵A(-4,0),O(0,0),C(2,6),∴AN的中点为( , ),OC中点为( , ),∴ 解得∴N(6,6),
解得∴N(-2,6),
②以AC、NO为对角线,此时AC中点与NO中点重合,同理可得:
③以AO、CN为对角线,此时AO中点与CN中点重合,同理可得: 解得∴N(-6,-6),综上所述,存在点H,使得以点A、O、C、N为顶点的四边形是平行四边形,点N的坐标为(6,6)或(-2,6)或(-6,-6).
(4)存在;以点A、O、C、N为顶点的四边形是平行四边形时,点N的坐标为(6,6)或(-2,6)或(-6,-6).
2. 如图,抛物线y=ax2+bx+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C连接AC.其中OC=OB,tan∠CAO=3.(1)求抛物线的解析式;
解:(1)∵抛物线解析式为y=ax2+bx+3,令x=0得y=3,∴点C坐标为(0,3),∵OC=OB=3,∴点B坐标为(3,0),
(2)点P是第一象限内抛物线上的一动点,点Q为线段PB的中点,求△CPQ面积的最大时P点坐标;
(3)将抛物线沿射线CB方向平移 个单位得新抛物线y′,点M为新抛物线y′的顶点,点D为新抛物线y′上任意一点,点N为x轴上一点.当以M、N、C、D为顶点的四边形是平行四边形时,请直接写出所有符合条件的点N的坐标.
∵ , ,∴xN=7,或 ,∴xN=5,∴点N坐标为(7,0)或(5,0),或 , ,得yD=-1,
3. 如图,二次函数y=ax2+bx+4的图象与x轴交于点A(-1,0),B(4,0),与y轴交于点C,P为线段AB上一动点,将射线PB绕P点逆时针方向旋转45°后与二次函数图象交于点Q.(1)求二次函数y=ax2+bx+4的表达式;
(2)当点P在二次函数对称轴上时,求此时PQ的长;
(2)如解图①,过点Q作QE⊥x轴于点E,作直线y=x+1交y轴于点F,
则F(0,1),且该直线过点A(-1,0),∵OA=OF,∠AOF=90°,∴∠OAF=∠BPQ=45°,∴PQ∥AF,设直线PQ的解析式为直线y=x+c,
(3)求线段PQ的最大值;
(4)二次函数对称轴上是否存在点D,使P、Q、B、D四点能构成平行四边形,若存在,请求出点D的坐标,若不存在,请说明理由.
如解图④,PQ为以P,Q,B,D四点为顶点的四边形的对角线时,DQ∥PB,DQ=PB.设P(r,0)(-1≤r≤4),设直线PQ的解析式为y=x+d,则r+d=0,即d=-r,∴直线PQ的解析式为y=x-r,由 ,解得 或 (不符合题意,舍去),∴Q( ),
∵PD=BQ,GD=EQ,∠PGD=∠BEQ=90°,∴Rt△PDG≌Rt△BQE,∴PG=BE,∴ ,解得r1= ,r2= (不符合题意,舍去),∴y= = ,
2024辽宁中考数学二轮专题复习 微专题 二次函数与矩形、菱形、正方形问题(课件): 这是一份2024辽宁中考数学二轮专题复习 微专题 二次函数与矩形、菱形、正方形问题(课件),共43页。PPT课件主要包含了例1题图①,例1题图②,例1题解图①,例1题解图②,例1题解图③,例1题解图④,例1题图③,例1题解图⑤,例1题解图⑥,例1题解图⑦等内容,欢迎下载使用。
2024辽宁中考数学二轮专题复习 微专题 二次函数与角度问题(课件): 这是一份2024辽宁中考数学二轮专题复习 微专题 二次函数与角度问题(课件),共57页。PPT课件主要包含了例1题图①,全等三角形对应角相等,例1题图②,例1题图③,例2题图①,例2题图②,例2题解图①,例2题图③,例2题图④,例2题解图③等内容,欢迎下载使用。
2024辽宁中考数学二轮专题复习 微专题 二次函数与等腰三角形问题(课件): 这是一份2024辽宁中考数学二轮专题复习 微专题 二次函数与等腰三角形问题(课件),共58页。PPT课件主要包含了垂直平分线中垂线,垂直平分线和对称轴,例2题图①,例2题图②,例2题图③,例2题图④,例2题图⑤,第1题图,备用图,第1题解图②等内容,欢迎下载使用。












