

人教版八年级数学下册重难点专题提升精讲精练专题05勾股定理的应用(含折叠、动点)重难点题型专训(原卷版+解析)
展开题型一 勾股定理应用之航海问题
题型二 勾股定理应用之梯子滑落高度问题
题型三 勾股定理应用之蚂蚁行程问题
题型四 勾股定理之旗杆高度问题
题型五 勾股定理之台阶上地毯长度问题
题型六 勾股定理之是否受台风影响问题
题型七 勾股定理之折叠问题
题型八 勾股定理之动点问题
【经典例题一 勾股定理之航海问题】
【例1】(2022秋·山东济南·九年级统考期末)如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里B.40海里C.80海里D.40海里
【变式训练】
【变式1】(2022秋·八年级课时练习)如图,一般客轮从小岛A沿东北方向航行,同时一艘补给船从小岛A正东方向相距(100+100),沿北偏西60°方向航行,与客轮同时到达C处给客轮进行补给,则客轮与补给船的速度之比为( )
A.:2B.:1C.:2D.:1
【变式2】(2022春·四川南充·八年级四川省南充市第九中学校考阶段练习)如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向上,轮船从B处继续向正东方向航行100海里到达C处时,测得小岛A在船的北偏东30°的方向上,于点D,则AD的长为______海里.
【变式3】(2022秋·河北邯郸·九年级邯郸市第二十三中学校考期末)在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
【经典例题二 勾股定理之梯子滑落高度问题】
【例2】(2022春·四川凉山·八年级校考阶段练习)如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE上的位置上,如图,测得DB的长0.5米,则梯子顶端A下落了( )米.
A.0.5B.0.4C.0.6D.1
【变式训练】
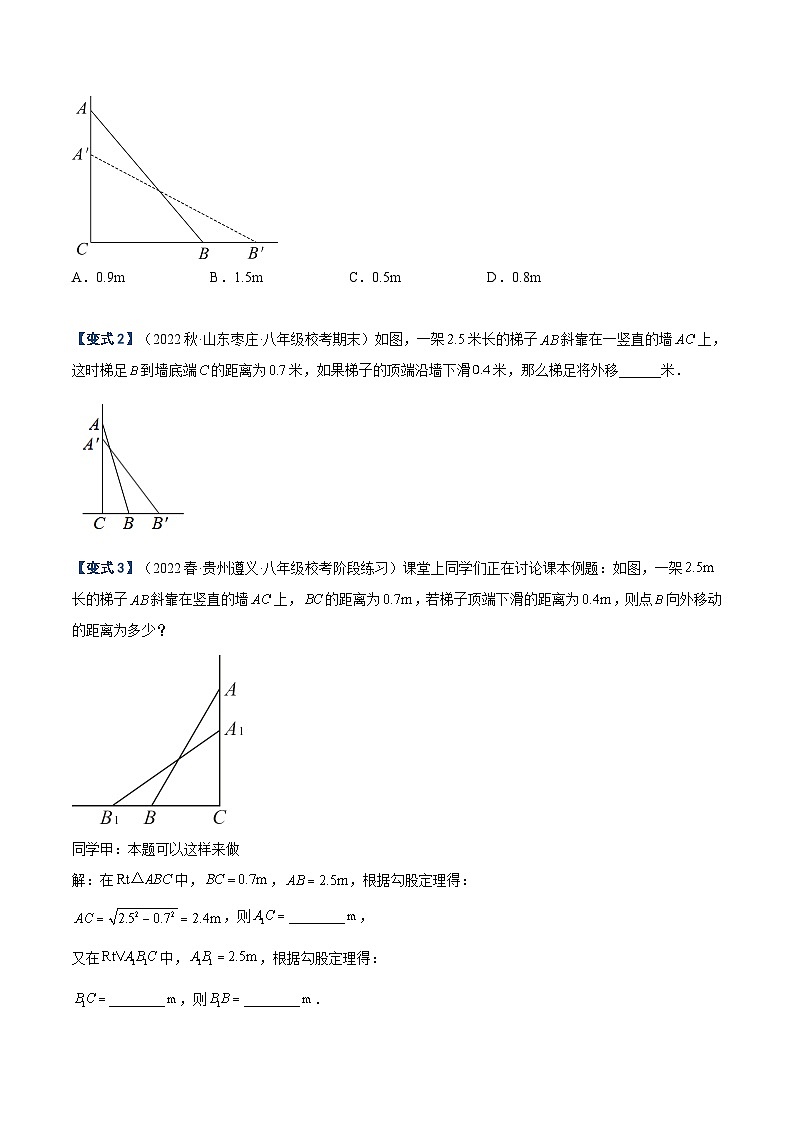
【变式1】(2022秋·全国·八年级期中)如图,一架2.5m长的梯子,斜立在一竖直的墙上,这时梯子的底部距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯子的底部将平滑( )
A.0.9mB.1.5mC.0.5mD.0.8m
【变式2】(2022秋·山东枣庄·八年级校考期末)如图,一架米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端沿墙下滑米,那么梯足将外移______米.
【变式3】(2022春·贵州遵义·八年级校考阶段练习)课堂上同学们正在讨论课本例题:如图,一架长的梯子斜靠在竖直的墙上,的距离为,若梯子顶端下滑的距离为,则点向外移动的距离为多少?
同学甲:本题可以这样来做
解:在中,,,根据勾股定理得:
,则________,
又在中,,根据勾股定理得:
________,则________.
同学乙.我发现在本题答案中,梯子顶端下滑的距离比末端向外移动的距离小,说明在梯子下滑时,梯子顶端下滑的距离一定比末端向外移动的距离小.
同学丙:不一定,我能举个反例,比如,当梯子顶端下滑的距离为时,
在中,,,根据勾股定理得:________,则
,
又在中,,根据勾股定理得:
________,则________.即:,
老师.通过上面的讨论,同学们发现有时大,有时大,那么有没有可能正好的情况存在呢?
同学丁:有.当梯子顶端从处下滑时,末端向外也移动.你认为他的说法正确吗?说明理由.
【经典例题三 勾股定理之蚂蚁行程问题】
【例3】(2023秋·河北保定·八年级校考期末)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A.B.3C.D.
【变式训练】
【变式1】(2021秋·山西太原·八年级校联考阶段练习)如图是一个长为12cm,宽为5cm,高为8cm的长方体,一只蜘蛛从一条侧棱的中点A沿着长方体表面爬行到顶点B去捕捉蚂蚁,此时蜘蛛爬行的最短距离是( )
A.13 cmB.15 cmC.21 cmD.25cm
【变式2】(2022秋·浙江·八年级专题练习)如图,一个长方体盒子紧贴地面,一只蚂蚁由出发,在盒子表面上爬到点,已知,,,这只蚂蚁爬行的最短路程是________.
【变式3】(2022春·广西百色·八年级统考期中)如图所示是一个三级台阶,它的每一级的长、宽、高分别等于7cm、6cm、2cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线有多长?
【经典例题四 勾股定理之旗杆高度问题】
【例4】(2022秋·广东深圳·八年级统考期末)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A.B.C.6D.
【变式训练】
【变式1】(2023秋·河南洛阳·八年级统考期末)为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米B.1.2 米C.1.25 米D.1.5 米
【变式2】(2020秋·八年级单元测试)如图所示,地面上竖立了一根木杆,顶端与地面上有绳索相连.在木杆的8米高处有两只猴子,一只猴子爬下木杆走到离木杆16米的处.另一只爬到杆顶后沿绳索滑至处,两只猴子所经过的路程相等,则这根木杆高__________米.
【变式3】(2022秋·江苏·八年级专题练习)太原的五一广场视野开阔,是一处设计别致,造型美丽的广场园林,成为不少市民放风筝的最佳场所,某校八年级(1)班的小明和小亮同学学习了“勾股定理”之后,为了测得图中风筝的高度,他们进行了如下操作:
①测得的长为15米(注:);
②根据手中剩余线的长度计算出风筝线的长为25米;
③牵线放风筝的小明身高1.7米.
(1)求风筝的高度.
(2)过点D作,垂足为H,求的长度.
【经典例题五 勾股定理之台阶上地毯长度问题】
【例5】(2022春·山东菏泽·八年级统考期中)某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要( )
A.2560元B.2620元C.2720元D.2840元
【变式训练】
【变式1】(2022秋·广东茂名·八年级校考期中)如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.5mB.6mC.7mD.8m
【变式2】(2021秋·山东青岛·八年级校考阶段练习)如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要____________元钱.
【变式3】(2021春·湖北武汉·八年级阶段练习)如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?
【经典例题六 勾股定理之是否受台风影响问题】
【例6】(2022秋·八年级课时练习)M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4B.5C.6D.7
【变式训练】
【变式1】(2022秋·重庆·八年级校联考期末)如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10B.7C.6D.12
【变式2】(2021秋·河南濮阳·九年级校考阶段练习)如图,铁路和公路在点处交汇,.公路上处距点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路上沿方向以36千米/时的速度行驶时,处受噪音影响的时间为______秒.
【变式3】(2022秋·四川达州·八年级校考期中)如图,,是两条公路相交成,沿公路方向离点米的点A处有一所学校,当重型运输卡车沿道路方向行驶时,在以重型运输卡车所在的点P为圆心、长为半径的圆形区域内都会受到卡车噪声的影响,且点P与点A的距离越近噪声影响越大.假设重型运输卡车沿着道路方向行驶的速度为18千米/小时.
(1)求对学校的噪声影响最大时,卡车与学校之间的距离(保留根号);(直角三角形中锐角所对的直角边等于斜边的一半).
(2)求卡车沿道路方向行驶一次给学校带来噪声影响的时间.
【经典例题七 勾股定理之折叠问题】
【例7】(2022秋·广东茂名·八年级信宜市第二中学校考期中)如图,等腰直角三角形纸片中,,把纸片沿对折后,点A恰好落在上的点D处,点,,则下列结论:;;与的周长相等.正确的个数是( )
A.0个B.1个C.2个D.3个
【变式训练】
【变式1】(2022秋·江苏·八年级统考期中)如图,三角形纸片中,点是边上一点,连接,把沿着直线翻折,得到,交于点,连接交于点,若,的面积为,则的长是( )
A.B.C.D.
【变式2】(2021秋·河南郑州·八年级校考期中)如图,在直角三角形纸片ABC中,∠C=90°,AC=12,BC=10,D是BC的中点,E是AC上的一个动点,将三角形纸片ABC沿DE折叠,连接AC′.当△AEC′是直角三角形时,CE的长为____________.
【变式3】(2022秋·江苏苏州·八年级苏州高新区第二中学校考阶段练习)操作与实践:已知长方形纸片中,,.
操作一:如图①,任意画一条线段,将纸片沿折叠,使点B落到点的位置,与交于点G.试说明重叠部分为等腰三角形;
操作二:如图②,将纸片沿对角线折叠,使点B落到点的位置,与交于点H.求的面积.
【经典例题八 勾股定理之动点问题】
【例8】(2023秋·重庆沙坪坝·八年级重庆南开中学校考期末)如图,在Rt△ABC中,∠ACB=90°, AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当∠DEB是直角时,DF的长为( ).
A.5B.3C.D.
【变式训练】
【变式1】(2022秋·浙江·八年级期中)如图,在中,是延长线上一点,是边上一动点, 连接,作与关于对称 (点与点对应),连接,则长的最小值是( )
A.B.C.D.
【变式2】(2022·贵州遵义·统考一模)如图,在中,,,,P为线段AB上一动点,以线段CP为边作等边三角形PCD,则点P从点A向点B运动的过程中,点D所经过的路径长为______.
【变式3】(2020秋·八年级校考阶段练习)如图,在四边形中,,,,若连接,沿翻折,则点A落在点M上.动点P从点C出发沿的路线运动,运动到点B停止.
(1)求的长度;
(2)当线段的中垂线经过点D时,求点P运动路线的长度;
(3)在点P的运动过程中,当为等腰三角形时,点P运动路线的长度为___________(直接写出答案)
【培优检测】
1.(2022秋·浙江宁波·八年级校考期中)如图,,点在内部,且,若、分别为边、上的动点,则周长的最小值为( )
A.4B.C.D.8
2.(2023春·八年级单元测试)1.如图,在中,,,,是的平分线,交于点,则的面积等于( )
A.B.C.D.
3.(2022秋·山东烟台·九年级统考期末)已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )
A.海里B.海里C.16海里D.24海里
4.(2023秋·河南南阳·八年级校考期末)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A.B.C.6D.
5.(2022春·四川泸州·八年级统考期末)我国古代数学专著《九章算术》里记载了这样一个问题“今有垣高一丈.倚木于垣,上与垣齐,引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,问木杆长多少尺?”(说明:1丈尺),此木杆的长度为( )
A.49尺B.49.5尺C.50尺D.50.5尺
6.(2022秋·山东淄博·七年级统考期中)如图,在四边形中,,,与关于直线轴对称,,,点与点对应,交于点,则线段的长为( )
A.5B.C.4D.
7.(2021秋·山东济南·八年级统考期中)如图,三级台阶的每一级的长、宽、高分别为.点A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )dm.
A.12B.10C.17D.25
8.(2022秋·八年级课时练习)如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2B.C.6D.8
9.(2022春·甘肃庆阳·八年级校考期中)如图,一个梯子长2.5米,顶端靠在墙上,这时梯子下端与墙角距离为0.7米,梯子滑动后停在的位置上,测得长为0.8米,求梯子顶端下落了_________米.
10.(2020秋·广东茂名·八年级校考阶段练习)如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,这棵树有的高是______________ .
11.(2022秋·山东济南·八年级济南市章丘区第四中学校考阶段练习)如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
12.(2022秋·八年级课时练习)将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值__,h的最大值__.
13.(2022秋·全国·八年级专题练习)如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点160米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心,100米为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为36千米/时,则对学校A的噪声影响最大时卡车P与学校A的距离是___米;重型运输卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间是____秒.
14.(2021春·四川成都·八年级校考期中)在等腰直角三角形中,,,是边上一点,且,是边上一点,将沿翻折,使点落在线段的点上,则_________.
15.(2021秋·广东佛山·八年级统考阶段练习)如图,一个梯子AB,顶端A靠在墙AC上,这是梯子的顶端距地面的垂直高度为24米,若梯子的顶端下滑4米,底端将水平滑动了8米,求滑动前梯子底端与墙的距离CB是多少?
16.(2022春·四川泸州·八年级统考阶段练习)如图,四边形为某街心公园的平面图,经测量米,米,且.
(1)求的度数;
(2)若为公园的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点处安装一个监控装置来监控道路的车辆通行情况,已知摄像头能监控的最大范围为周围的100米(包含100米),求被监控到的道路长度为多少?
17.(2022秋·江苏宿迁·八年级统考期中)如图1,直线,垂足为O,直线l分别与射线、相交于点A、B,且,,连接.
(1)求线段的长;
(2)若点C为直线l上的一个动点,求点O到点C的距离的最小值;
(3)如图2,将沿直线l折叠,点O落在点D处,,垂足为点E,求的长;
(4)若点F为直线或上的一个动点,使得以A、B、F为顶点的三角形是等腰三角形,则满足条件的所有点F的个数为______个.
18.(2022秋·陕西西安·八年级校考阶段练习)如图1,在中,,,,点为边上一动点,将沿直线折叠,得到,请解决下列问题.
(1)______;当点恰好落在斜边上时,______;
(2)连接,当是以为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点到直线的距离;
(3)如图3,为边上一点,且,连接,当为直角三角形时,______.(请写出所有满足条件的长)
19.(2023春·全国·八年级专题练习)如图,点是等腰直角的直角边上的一点,AE的中垂线分别交,,于点,,,且.
(1)求的度数.
(2)若,求的长.
(3)若平分,则:
①判断线段与的位置关系并证明.
②求出的长.
20.(2021秋·江苏无锡·八年级校联考期中)如图1,在长方形中,BC=3,动点从出发,以每秒1个单位的速度,沿射线方向移动,作关于直线的对称,设点的运动时间为
(1)当P点在线段BC上且不与C点重合时,若直线PB’与直线CD相交于点M,且∠PAM=45°,试求:AB的长
(2)若AB=4
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
专题05 勾股定理的应用(含折叠、动点)重难点题型专训
【题型目录】
题型一 勾股定理应用之航海问题
题型二 勾股定理应用之梯子滑落高度问题
题型三 勾股定理应用之蚂蚁行程问题
题型四 勾股定理之旗杆高度问题
题型五 勾股定理之台阶上地毯长度问题
题型六 勾股定理之是否受台风影响问题
题型七 勾股定理之折叠问题
题型八 勾股定理之动点问题
【经典例题一 勾股定理之航海问题】
【例1】(2022秋·山东济南·九年级统考期末)如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A.40海里B.40海里C.80海里D.40海里
【答案】B
【分析】过点P作PC⊥AB,则在中,通过30°的直角三角形,计算出PC的长,再根据等腰直角三角形,通过勾股定理即可求出PB.
【详解】解:作PC⊥AB于C点,
∵A在P的北偏东30°方向,
∴,
∴,
又∵B在P的南偏东45°方向上,
∴,
∴,
∴∠APC=60°,∠BPC=45°,AP=80(海里)
∴在中,,
∴(海里)
∵在中,∠BPC=45°,
∴三角形为等腰直角三角形,
∴,
∴(海里).
故选:B.
【点睛】本题考查方位角有关的计算以及用勾股定理求航海问题,解决本题的关键是构建直角三角形进行计算.
【变式训练】
【变式1】(2022秋·八年级课时练习)如图,一般客轮从小岛A沿东北方向航行,同时一艘补给船从小岛A正东方向相距(100+100),沿北偏西60°方向航行,与客轮同时到达C处给客轮进行补给,则客轮与补给船的速度之比为( )
A.:2B.:1C.:2D.:1
【答案】A
【分析】过C作CD⊥AB于D,设AD=x,根据特殊三角形的性质,分别用含x的代数式表示出CD,BD,根据AB的长求出x,再根据勾股定理求出AC,BD,即可得到答案.
【详解】解:过C作CD⊥AB于D,
设AD=x,
由题意得∠CAD=45°,∠NBC=60°,
在Rt△ACD中,∠ACD=90°-45°=45°,
∴∠ACD=∠CAD,
∴CD=AD=x,
∴ ,
在Rt△BCD中,∠CBD=90°-60°=30°,
∴BC=2CD=2x,
∴ ,
∵AB=100+100 ,
∴AD+BD=x+x=100+100,
∴(1+)x=100(1+),
∴x=100,
即AD=100海里,
∴AC=100海里,BC=200海里,
∵时间一定时速度与路程成正比,
∴客轮与补给船的速度之比为100:200=:2,
故选:A.
【点睛】本题主要考查了解直角三角形的应用,正确作出辅助线,构造出直角三角形是解决问题的关键.
【变式2】(2022春·四川南充·八年级四川省南充市第九中学校考阶段练习)如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向上,轮船从B处继续向正东方向航行100海里到达C处时,测得小岛A在船的北偏东30°的方向上,于点D,则AD的长为______海里.
【答案】
【分析】如图,和有公共边,在两个直角三角形中,利用三角函数即可用表示出与,根据即可列方程,从而求得的长.
【详解】如图所示:
则,
∴,
∴海里.
在中,设海里,则海里,
,
在中, , ,
又∵,
∴,
解得:,
∴海里
故答案为:
【点睛】本题主要考查了勾股定理的应用、直角三角形的计算,一般的三角形可以通过作高线转化为解直角三角形的计算,计算时首先计算直角三角形的公共边是常用的思路.
【变式3】(2022秋·河北邯郸·九年级邯郸市第二十三中学校考期末)在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
【答案】(1)海里
(2)救助船先到达,计算过程见解析
【分析】(1)如图,作于,在中先求出的长,继而在中求出的长即可;
(2)根据“时间=路程÷速度”分别求出救助船A和救助船B所需的时间,进行比较即可.
【详解】(1)解:如图,过点P作于,
∴,
由题意得:海里,,,
∴海里,是等腰直角三角形,
∴海里,海里,
答:收到求救讯息时事故渔船与救助船之间的距离为海里;
(2)解:∵海里,海里,救助船分别以20海里/小时、15海里/小时的速度同时出发,
∴救助船所用的时间为(小时),
救助船所用的时间为(小时),
∵,
∴救助船先到达.
【点睛】本题考查了解直角三角形的应用,涉及了含30度角的直角三角形的性质,等腰直角三角形的判定,勾股定理的应用等,熟练正确添加辅助线构建直角三角形是解题的关键.
【经典例题二 勾股定理之梯子滑落高度问题】
【例2】(2022春·四川凉山·八年级校考阶段练习)如图所示,一个梯子AB长2.5米,顶端A靠墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE上的位置上,如图,测得DB的长0.5米,则梯子顶端A下落了( )米.
A.0.5B.0.4C.0.6D.1
【答案】A
【分析】在直角三角形ABC中,根据勾股定理,得:AC=2米,由于梯子的长度不变,在直角三角形CDE中,根据勾股定理,得CE=1.5米,所以AE=0.5米,即梯子的顶端下滑了0.5米.
【详解】解:∵在Rt△ABC中,AC⊥BC,
∴,
∵AB=2.5米,BC=1.5米,
∴AC===2米.
∵Rt△ECD中,CE⊥CD,
∴,
∵AB=DE=2.5米,CD=(1.5+0.5)米,
∴EC===1.5米,
∴AE=AC﹣CE=2﹣1.5=0.5米.
故选:A.
【点睛】本题主要考查了勾股定理,解题时注意梯子的长度不变,分别运用勾股定理求得AC和CE的长是解题的关键.
【变式训练】
【变式1】(2022秋·全国·八年级期中)如图,一架2.5m长的梯子,斜立在一竖直的墙上,这时梯子的底部距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯子的底部将平滑( )
A.0.9mB.1.5mC.0.5mD.0.8m
【答案】D
【分析】先根据梯子的顶端下滑了0.4m求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.
【详解】∵在Rt△ABC中,AB=2.5m,BC=0.7m,
∴AC===2.4m,
∵梯子的顶端下滑了0.4m,
∴A′C=2m,
∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,
∴B′C===1.5m,
∴BB′=B′C﹣BC=1.5﹣0.7=0.8m.
故选:D.
【点睛】此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
【变式2】(2022秋·山东枣庄·八年级校考期末)如图,一架米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端沿墙下滑米,那么梯足将外移______米.
【答案】
【分析】在直角三角形中,已知,根据勾股定理即可求的长度,根据即可求得的长度,在直角三角形中,已知,即可求得的长度,根据即可求得的长度.
【详解】解;在直角中,已知, ,
则,
,
在直角中,,且为斜边,
,
梯足向外移动了.
故填.
【点睛】本题考查了勾股定理在实际生活中的应用,考查了勾股定理在直角三角形中的正确运用,本题中求的长度是解题的关键.
【变式3】(2022春·贵州遵义·八年级校考阶段练习)课堂上同学们正在讨论课本例题:如图,一架长的梯子斜靠在竖直的墙上,的距离为,若梯子顶端下滑的距离为,则点向外移动的距离为多少?
同学甲:本题可以这样来做
解:在中,,,根据勾股定理得:
,则________,
又在中,,根据勾股定理得:
________,则________.
同学乙.我发现在本题答案中,梯子顶端下滑的距离比末端向外移动的距离小,说明在梯子下滑时,梯子顶端下滑的距离一定比末端向外移动的距离小.
同学丙:不一定,我能举个反例,比如,当梯子顶端下滑的距离为时,
在中,,,根据勾股定理得:________,则
,
又在中,,根据勾股定理得:
________,则________.即:,
老师.通过上面的讨论,同学们发现有时大,有时大,那么有没有可能正好的情况存在呢?
同学丁:有.当梯子顶端从处下滑时,末端向外也移动.你认为他的说法正确吗?说明理由.
【答案】,,;,,;丁的说法正确,理由见解析
【分析】在中,根据勾股定理求出的值,从而得到的值,在中,根据勾股定理求出的值,即可得出的值;再根据同学甲、乙、丁的情况给出的数值分别代入求解即可.
【详解】解:同学甲:在中,,,
根据勾股定理,得,
则,
又在中,,
根据勾股定理,得,则.
故答案为:;;.
同学丙:在中,,,
根据勾股定理,得,
则,
又在中,,
根据勾股定理,得,
则.即.
故答案为:;;.
同学丁:说法正确,理由如下:
在中,,,
根据勾股定理,得,
则,
又在中,,
根据勾股定理,得,
则,即.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理是解题的关键.
【经典例题三 勾股定理之蚂蚁行程问题】
【例3】(2023秋·河北保定·八年级校考期末)如图是楼梯的一部分,若,,,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )
A.B.3C.D.
【答案】D
【分析】此类题目只需要将其展开便可直观的得出解题思路.将台阶展开得到的是一个矩形,蚂蚁要从A点到C点的最短距离,便是矩形的对角线,利用勾股定理即可解出答案.
【详解】解:将台阶展开,如图,
因为DC=AE+BE=3+1=4,AD=2,
所以AC2=DC2+AD2=20,
所以AC=,
故选:D.
【点睛】本题考查了平面展开-最短路径问题,用到台阶的平面展开图,根据题意判断出长方形的长和宽是解题的关键.
【变式训练】
【变式1】(2021秋·山西太原·八年级校联考阶段练习)如图是一个长为12cm,宽为5cm,高为8cm的长方体,一只蜘蛛从一条侧棱的中点A沿着长方体表面爬行到顶点B去捕捉蚂蚁,此时蜘蛛爬行的最短距离是( )
A.13 cmB.15 cmC.21 cmD.25cm
【答案】B
【分析】先将长方体沿CF、FG、GD剪开,向上翻折,使面FCDG和面BDCE在同一个平面内,连接AB;或将长方体沿CD、CF、FG剪开,向右翻折,使面CFGD和面GHBD在同一个平面内,连接AB;或将长方体沿CD、DB、BE剪开,向上翻折,使面DBEC和面CEMF在同一个平面内,连接AB,然后分别在Rt△ABE、Rt△ABC和Rt△ABD中利用勾股定理求得AB的长,比较大小即可求得需要爬行的最短路程.
【详解】
将长方体沿CF、FG、GD剪开,向上翻折,使面FCDG和面BDCE在同一个平面内,如图1:,.
∴在Rt△ABE中,
将长方体沿CD、CF、FG剪开,向右翻折,使面CFGD和面GHBD在同一个平面内,如图2:,
∴在Rt△ABC中,
将长方体沿CD、DB、BE剪开,向上翻折,使面DBEC和面CEMF在同一个平面内,如图3:,
∴在Rt△ABD中,
∵
∴蜘蛛爬行的最短距离是15cm.
故选:B.
【点睛】此题考查了勾股定理在最短路径问题中的应用,利用了转化思想,解题的关键是将立体图形展为平面图形并利用勾股定理的知识求解.
【变式2】(2022秋·浙江·八年级专题练习)如图,一个长方体盒子紧贴地面,一只蚂蚁由出发,在盒子表面上爬到点,已知,,,这只蚂蚁爬行的最短路程是________.
【答案】
【分析】将长方体盒子按不同方式展开,得到不同的长方形,求出不同长方形的对角线,最短者即为正确答案.
【详解】解:由题意,
如图所示,
得;
如图所示,
得,
如图3所示,
,
∴蚂蚁爬行的最短路程是10.
故答案为:10.
【解答】本题考查了勾股定理的应用,根据题意将长方体盒子展开为平面图形,根据勾股定理求出最短路程进行比较是解题关键.
【变式3】(2022春·广西百色·八年级统考期中)如图所示是一个三级台阶,它的每一级的长、宽、高分别等于7cm、6cm、2cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线有多长?
【答案】25cm
【分析】展开后得到直角三角形ACB,根据题意求出AC、BC,根据勾股定理求出AB即可.
【详解】解:如图,将台阶展开,
由题意得;AC=6×3+2×3=24,BC=7,.
所以由勾股定理得:AB2=AC2+BC2=625,
即AB=25(cm),
答:蚂蚁爬行的最短线路为25cm.
【点睛】本题主要考查对勾股定理,平面展开——最短路径问题等知识点的理解和掌握,能理解题意知道是求出直角三角形ABC的斜边AB的长是解此题的关键.
【经典例题四 勾股定理之旗杆高度问题】
【例4】(2022秋·广东深圳·八年级统考期末)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A.B.C.6D.
【答案】B
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,即可得到结论.
【详解】解:设秋千绳索的长度为,
由题意可得,
四边形为矩形,,,,,
∴,,
在中,,
即,
解得,
即的长度为.
故选:B.
【点睛】本题主要考查了勾股定理的应用,正确理解题意,掌握直角三角形中两直角边的平方和等于斜边的平方是解题的关键.
【变式训练】
【变式1】(2023秋·河南洛阳·八年级统考期末)为预防新冠疫情,民生大院入口的正上方 A 处装有红外线激光测温仪(如图所示),测温仪离地面的距离 AB=2.4 米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为 1.8 米的市民 CD 正对门缓慢走到离门 0.8 米的地方时(即 BC=0.8 米),测温仪自动显示体温,则人头顶离测温仪的距离 AD 等于( )
A.1.0 米B.1.2 米C.1.25 米D.1.5 米
【答案】A
【分析】过点D作于点E,构造,利用勾股定理解得AD的长即可.
【详解】解:过点D作于点E,
中
(米)
故选:A.
【点睛】本题考查勾股定理的应用,作出正确的辅助线是解题关键.
【变式2】(2020秋·八年级单元测试)如图所示,地面上竖立了一根木杆,顶端与地面上有绳索相连.在木杆的8米高处有两只猴子,一只猴子爬下木杆走到离木杆16米的处.另一只爬到杆顶后沿绳索滑至处,两只猴子所经过的路程相等,则这根木杆高__________米.
【答案】12
【分析】阅读题目信息可得两只猴子所经过的距离相等是指BD+AD=BC+AC=24,设BD=x,根据勾股定理列方程求解.
【详解】设BD=x米,根据题意可得BD+AD=BC+AC,x+AD=8+16,
∴AD=24-x,
在RtΔACD中,由勾股定理得,,
∴
解得,x=4
∴DC=x+8=4+8=12米,
即这根木杆高12米.
【点睛】本题考查勾股定理的实际应用,通过图形找到等量关系列方程是解答此题的关键.
【变式3】(2022秋·江苏·八年级专题练习)太原的五一广场视野开阔,是一处设计别致,造型美丽的广场园林,成为不少市民放风筝的最佳场所,某校八年级(1)班的小明和小亮同学学习了“勾股定理”之后,为了测得图中风筝的高度,他们进行了如下操作:
①测得的长为15米(注:);
②根据手中剩余线的长度计算出风筝线的长为25米;
③牵线放风筝的小明身高1.7米.
(1)求风筝的高度.
(2)过点D作,垂足为H,求的长度.
【答案】(1)风筝的高度为21.7米
(2)的长度为9米
【分析】(1)在中由勾股定理求得CD的长,再加上DE即可;
(2)利用等积法求出DH的长,再在在中由勾股定理即可求得BH的长.
【详解】(1)在中,由勾股定理,得:
(米),
所以(米),
答:风筝的高度为21.7米.
(2)由等积法知:,
解得:(米).
在中,(米),
答:的长度为9米.
【点睛】本题考查了勾股定理的实际应用,正确运用勾股定理是关键,注意计算准确.
【经典例题五 勾股定理之台阶上地毯长度问题】
【例5】(2022春·山东菏泽·八年级统考期中)某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要( )
A.2560元B.2620元C.2720元D.2840元
【答案】C
【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
【详解】
利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为米、5米,
∴地毯的长度为12+5=17米,地毯的面积为17×2=34平方米,
∴购买这种地毯至少需要80×34=2720元.
故选C.
【点睛】本题考查的知识点是勾股定理的应用,生活中的平移现象,解题关键是要注意利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
【变式训练】
【变式1】(2022秋·广东茂名·八年级校考期中)如图所示:是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.5mB.6mC.7mD.8m
【答案】C
【详解】楼梯竖面高度之和等于BC的长,横面宽度之和等于AB的长.
由于,
所以至少需要地毯长4+3=7(m).
故选C
【变式2】(2021秋·山东青岛·八年级校考阶段练习)如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要____________元钱.
【答案】612
【分析】先由勾股定理求出BC的长为12m,再用(AC+BC)乘以2乘以18即可得到答案.
【详解】如图,∵∠C=90,AB=13m,AC=5m,
∴BC==12m,
∴(元).
故填:612.
【点睛】此题考查勾股定理、平移的性质,题中求出地毯的总长度是解题的关键,地毯的长度由平移可等于楼梯的垂直高度和水平距离的和,进而求得地毯的面积.
【变式3】(2021春·湖北武汉·八年级阶段练习)如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?
【答案】612元.
【详解】本题考查的是勾股定理的应用
地毯的长是楼梯的竖直部分与水平部分的和,即AC与BC的和,在直角△ABC中,根据勾股定理即可求得BC的长,地毯的长与宽的积就是面积.
如图,
由题意得,,
则地毯总长为,
则地毯的总面积为,
所以铺完这个楼道至少需要元.
【经典例题六 勾股定理之是否受台风影响问题】
【例6】(2022秋·八年级课时练习)M 城气象中心测得台风中心在 M 城正北方向 240km 的 P 处,以每小时 45km 的速度向南偏东 30°的 PB 方向移动,距台风中心 150km 的范围内是受台风影响的区域,则 M 城 受台风影响的时间为( )小时.
A.4B.5C.6D.7
【答案】A
【分析】如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km,求出FH,然后利用时间=路程÷速度,计算即可解决问题.
【详解】解:如图,过点M作ME⊥PB,在BP上取点F,H,设MF=MH=150km
在Rt△PME中,∵∠MEP=90°,PM=240km,∠MPB=30°,
∴ME=PM=120km,
∴EF=EH==90(km),
∴FH=180km,
∴受台风影响的时间有180÷45=4(小时).
故选:A
【点睛】本题考查解直角三角形的应用-方向角问题,解题的关键是理解题意,学会添加常用辅助线根据直角三角形解决问题,属于中考常考题型.
【变式训练】
【变式1】(2022秋·重庆·八年级校联考期末)如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10B.7C.6D.12
【变式2】(2021秋·河南濮阳·九年级校考阶段练习)如图,铁路和公路在点处交汇,.公路上处距点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路上沿方向以36千米/时的速度行驶时,处受噪音影响的时间为______秒.
【答案】32
【分析】如图,首先过点作,求出最短距离的长度,然后在上取点,使得,根据勾股定理得出的长度,即可求出的长度,然后计算出时间即可.
【详解】解:如图,过点作,
米,
米米,
在上取点,使得,当火车在上时,处受噪音影响,
米,
由勾股定理得米,米,
即米,
36千米/时10米/秒,
处受噪音影响的时间为:秒,
故答案为:32.
【点睛】本题主要考查了勾股定理,解题的关键在于准确找出受影响的路段,从而利用勾股定理求出其长度.
【变式3】(2022秋·四川达州·八年级校考期中)如图,,是两条公路相交成,沿公路方向离点米的点A处有一所学校,当重型运输卡车沿道路方向行驶时,在以重型运输卡车所在的点P为圆心、长为半径的圆形区域内都会受到卡车噪声的影响,且点P与点A的距离越近噪声影响越大.假设重型运输卡车沿着道路方向行驶的速度为18千米/小时.
(1)求对学校的噪声影响最大时,卡车与学校之间的距离(保留根号);(直角三角形中锐角所对的直角边等于斜边的一半).
(2)求卡车沿道路方向行驶一次给学校带来噪声影响的时间.
【答案】(1)40米
(2)卡车沿道路方向行驶一次给学校带来噪声影响的时间为12秒
【分析】(1)过点A作于H,利用含30°角的直角三角形的性质可得答案;
(2)当米时,则卡车在段对学校A有影响,利用勾股定理求出的长,再根据等腰三角形的性质可得的长,从而求出时间.
【详解】(1)解:过点A作于H,
∵,米,
∴米,
∴对学校的噪声影响最大时,卡车与学校之间的距离为40米;
(2)解:如图,当米时,则卡车在CD段对学校A有影响,
由(1)知米,
∴(米),
∵,
∴(米),
∵重型运输卡车行驶的速度为18千米/小时,即米/秒,
∴(秒),
∴卡车沿道路方向行驶一次给学校带来噪声影响的时间为12秒.
【点睛】本题主要考查了勾股定理的实际应用,含角的直角三角形的性质,等腰三角形的性质,垂线段最短等知识,根据题意构造出直角三角形是解题的关键.
【经典例题七 勾股定理之折叠问题】
【例7】(2022秋·广东茂名·八年级信宜市第二中学校考期中)如图,等腰直角三角形纸片中,,把纸片沿对折后,点A恰好落在上的点D处,点,,则下列结论:;;与的周长相等.正确的个数是( )
A.0个B.1个C.2个D.3个
【答案】D
【分析】在等腰中,可得,即,由折叠可得,,即,则有,可判断正确;根据,,可得,,即正确;根据的周长为:,由折叠可得,,则有的周长为:,可得正确,即问题得解.
【详解】在等腰中,∠C=90°,,
∴,,
∴,
∵,
∴,
即由折叠可得,,
∴在中,,
∴,
∴,故正确;
∵,,
∴,,
∴,故正确;
∵,,
∴,
∵的周长为:,
由折叠可得,,
∴的周长为:,
∴与的周长相等,故正确;
即正确的有三个,
故选:D.
【点睛】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.还考查了等腰直角三角形的性质,勾股定理的知识,掌握折叠的性质以及勾股定理是解答本题的关键.
【变式训练】
【变式1】(2022秋·江苏·八年级统考期中)如图,三角形纸片中,点是边上一点,连接,把沿着直线翻折,得到,交于点,连接交于点,若,的面积为,则的长是( )
A.B.C.D.
【答案】B
【分析】利用折叠和中线的性质,得到的面积,利用勾股定理求出,利用三角形的面积公式求出,进而求出,再利用勾股定理求出即可.
【详解】解:∵
∴为的中线,
∴,
∵翻折,
∴,,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
故选B.
【点睛】本题考查勾股定理与折叠问题.熟练掌握折叠的性质以及三角形的中线平分面积,以及勾股定理是解题的关键.
【变式2】(2021秋·河南郑州·八年级校考期中)如图,在直角三角形纸片ABC中,∠C=90°,AC=12,BC=10,D是BC的中点,E是AC上的一个动点,将三角形纸片ABC沿DE折叠,连接AC′.当△AEC′是直角三角形时,CE的长为____________.
【答案】或5
【分析】分两种情形,当∠AC'E=90°或∠AEC'=90°时,分别画出图形来解答.
【详解】解:当∠AC'E=90°时,
∵将△CDE沿DE折叠到△C′DE,
∴∠EC'D=∠C=90°,
∴∠AC'E+∠EC'D=180°,
∴点A、C'、D三点共线,
∵AC=12,BC=10,CD=BC=5
由勾股定理得AD= ,
设CE=C'E=x,则AE=12-x,AC'=13-5=8,
在Rt△AC'E中,由勾股定理得:
(12-x)2=82+x2,
解得x=,
∴CE=,
当∠AEC'=90°时,
∴∠CEC'=90°,
∴∠CED=45°,
∴CE=CD=5,
∠EAC'不可能为90°,
综上,CE=5或.
故答案为:5或.
【点睛】本题主要考查了翻折的性质,勾股定理等知识,解题的关键是学会运用分类讨论的思想思考问题,属于中考常考题型.
【变式3】(2022秋·江苏苏州·八年级苏州高新区第二中学校考阶段练习)操作与实践:已知长方形纸片中,,.
操作一:如图①,任意画一条线段,将纸片沿折叠,使点B落到点的位置,与交于点G.试说明重叠部分为等腰三角形;
操作二:如图②,将纸片沿对角线折叠,使点B落到点的位置,与交于点H.求的面积.
【答案】操作一:见解析;操作二:
【分析】操作一:由翻折的性质可知,由长方形的性质和平行线的性质可知,从而得到,由等角对等边可得;
操作二:首先表示出,然后在中利用勾股定理构建方程求出即可解决问题.
【详解】操作一:由折叠的性质可知,
∵在长方形中,
∴,
∴,
∴,
∴为等腰三角形;
操作二:在长方形中,,
同操作一可得,则,
在中,,
∴,
解得:,
∴.
【点睛】本题考查了折叠的性质,平行线的性质,等腰三角形的判定以及勾股定理的应用等知识,利用勾股定理构建出方程是解题的关键.
【经典例题八 勾股定理之动点问题】
【例8】(2023秋·重庆沙坪坝·八年级重庆南开中学校考期末)如图,在Rt△ABC中,∠ACB=90°, AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当∠DEB是直角时,DF的长为( ).
A.5B.3C.D.
【答案】C
【分析】如图,由题意知,,,,可知三点共线,与重合,在中,由勾股定理得,求的值,设,,在中,由勾股定理得,计算求解即可.
【详解】解:如图,
∵是直角
∴
由题意知,,
∴
∴三点共线
∴与重合
在中,由勾股定理得
设,
在中,由勾股定理得即
解得
∴的长为
故选C.
【点睛】本题考查了折叠的性质,勾股定理等知识.解题的关键在于明确三点共线,与重合.
【变式训练】
【变式1】(2022秋·浙江·八年级期中)如图,在中,是延长线上一点,是边上一动点, 连接,作与关于对称 (点与点对应),连接,则长的最小值是( )
A.B.C.D.
【答案】C
【分析】如图,过点A作AE⊥BC于点E,当点A在DM的上时AD的值最小,根据勾股定理依次求出AE,CE,AM,DM的长,即可解决问题.
【详解】解:如图,过点A作AE⊥BC于点E,连接MA,
∵AD≥MD-AM
当点A在DM上时AD的值最小,如图,
∵CM=2,BC=3,
∴BM=BC+CM=5,
由折叠得:DM=BM=5,
∵∠B=60°,
∴∠,
又∵,
∴,
在中中,
∵,
∴,
∴,
在中,
∵,
∴,
∴最小=.
故选C.
【点睛】本题主要考查了翻折变换的性质,勾股定理,最值问题等知识,两边之差小于第三边,解题的关键是作出辅助线,从整体上把握题意,准确找到图形中数量关系.
【变式2】(2022·贵州遵义·统考一模)如图,在中,,,,P为线段AB上一动点,以线段CP为边作等边三角形PCD,则点P从点A向点B运动的过程中,点D所经过的路径长为______.
【答案】4
【分析】由点P从点A向点B运动可知,画出P点在A点时D点的位置,在B点时D的位置,发现D点的经过的路径长即是D1D2的长;
【详解】在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,
∴AB=2AC=2×2=4,
∠BAC=90°-30°=60°,
故当点P位于A点时,点D位于点D1,
∴△CAD1为等边三角形,
∴AD1=AC=2,
∴BD1=AB-AD1=4-2=2,
当点P位于点B时,点D位于点D2,
∴△CBD2是等边三角形,
∴BD2=CB,∠CBD2=60°,
∴∠ABD2=∠ABC+∠CBD2=90°,
∴△D1D2B是直角三角形,
在Rt△ABC中,BC==2,
∴BD2=2,
∴D1D2==4.
【点睛】本题考查动点问题,等边三角形的性质和勾股定理;熟练掌握等边三角形的性质是解决本题的关键.
【变式3】(2020秋·八年级校考阶段练习)如图,在四边形中,,,,若连接,沿翻折,则点A落在点M上.动点P从点C出发沿的路线运动,运动到点B停止.
(1)求的长度;
(2)当线段的中垂线经过点D时,求点P运动路线的长度;
(3)在点P的运动过程中,当为等腰三角形时,点P运动路线的长度为___________(直接写出答案)
【答案】(1)
(2)点P运动路线的长度为或时,的中垂线过点D;
(3)5或8或或
【分析】(1)证明出四边形为正方形,利用勾股定理即可求解;
(2)根据等腰三角形三线合一的性质来判断,需要分两种情况讨论,当时,即,为等腰三角形,当点与点重合时,,为等腰三角形,根据三线合一知的中垂线,过点D;
(3)连接,根据已知分析可得满足等腰三角形的多种情况:或,然后根据勾股定理进行分析计算.
【详解】(1)解:沿翻折,则点A落在点M上,
,
,,
四边形为正方形,
,
;
(2)解:需要分两种情况讨论,
当时,即,
为等腰三角形,
根据三线合一知的中垂线,过点D,
此时点P运动路线的长度为,
当点与点重合时,,
为等腰三角形,
根据三线合一知的中垂线,过点D,
此时点P运动路线的长度为,
综上所述:点P运动路线的长度为或时,的中垂线过点D;
(3)解:根据已知得,,则四边形是平行四边形.
又,根据勾股定理,得.
①作的中垂线交于,则是等腰三角形,此时,,即点P运动路线的长度5;
②当时,是等腰三角形,即点P运动路线的长度8;
③当点在上,时,,即点P运动路线的长度;
④当点在上,时,,即点P运动路线的长度;
故答案为:5或8或或.
【点睛】此题主要考查梯形的性质及等腰梯形的判定的理解及应用、勾股定理,解题的关键是注意分类讨论数学方法的运用.
【培优检测】
1.(2022秋·浙江宁波·八年级校考期中)如图,,点在内部,且,若、分别为边、上的动点,则周长的最小值为( )
A.4B.C.D.8
【答案】B
【分析】作关于对称点,作关于对称点,连接交于,交于,根据对称性可知, ,,从而的周长,根据两点之间线段最短,得到周长的最小值为, 在中,根据勾股定理求,从而确定答案.
【详解】解:作关于对称点,作关于对称点,连接交于,交于,如图所示:
根据对称性可知, ,,
的周长,
根据两点之间线段最短,周长的最小值为,
在中,,,根据勾股定理得,
故选:B.
【点睛】本题考查动点最值问题,涉及轴对称-最短周长问题、等腰直角三角形的判定与性质、勾股定理求线段长,熟练掌握利用对称性解决最短周长问题是解决问题的关键.
2.(2023春·八年级单元测试)1.如图,在中,,,,是的平分线,交于点,则的面积等于( )
A.B.C.D.
【答案】A
【分析】过点D作,先由等腰直角三角形性质求出,再证明,设,则,所以,解得: ,即,然后根据三角形面积公式求解即可.
【详解】解:过点D作,
∵在中,,,
∴,,
∴是等腰直角三角形,
∵是的平分线,
∴,
设,则,
∴,解得: ,
∴的面积,
故选:A.
【点睛】本题考查角平分线的性质,等腰直角三角形性质和判定,勾股定理,三角形面积公式,熟练掌握角平分线的性质是解题的关键.
3.(2022秋·山东烟台·九年级统考期末)已知,一轮船以16海里时的速度从港口A出发向北偏东方向航行,另一轮船以8海里时的速度同时从港口A出发向南偏东方向航行,则离开港口1小时后,两船相距( )
A.海里B.海里C.16海里D.24海里
【答案】B
【分析】根据方位角可知两船所走的方向夹角,再根据路程速度时间,得到,,最后利用勾股定理,即可求得两条船之间的距离.
【详解】解:由题意可知,,
离开港口1小时后,两艘船分别行驶了16海里和8海里,
即,,
由勾股定理得:,
故两船相距海里,
故选B.
【点睛】本题考查了勾股定理,方位角问题,熟练运用勾股定理进行计算是解题关键,基础知识,比较简单.
4.(2023秋·河南南阳·八年级校考期末)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A.B.C.6D.
【答案】B
【分析】设秋千的绳索长为,根据题意可得,利用勾股定理可得,即可得到结论.
【详解】解:设秋千绳索的长度为,
由题意可得,
四边形为矩形,,,,,
∴,,
在中,,
即,
解得,
即的长度为.
故选:B.
【点睛】本题主要考查了勾股定理的应用,正确理解题意,掌握直角三角形中两直角边的平方和等于斜边的平方是解题的关键.
5.(2022春·四川泸州·八年级统考期末)我国古代数学专著《九章算术》里记载了这样一个问题“今有垣高一丈.倚木于垣,上与垣齐,引木却行一尺,其木至地.问木长几何?”其内容可以表述为:“有一面墙,高1丈,将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,问木杆长多少尺?”(说明:1丈尺),此木杆的长度为( )
A.49尺B.49.5尺C.50尺D.50.5尺
【答案】D
【分析】当木杆的上端与墙头平齐时,木杆与墙、地面构成直角三角形,设木杆长为尺,则木杆底端离墙有尺,根据勾股定理可列出方程,解方程即可
【详解】如图,设木杆长为尺,则木杆底端B离墙的距离即的长有尺,
在中,
∵,
∴,
解得:
故选:D.
【点睛】本题考查了勾股定理的应用,解题的关键是由实际问题抽象出直角三角形,从而运用勾股定理解题.
6.(2022秋·山东淄博·七年级统考期中)如图,在四边形中,,,与关于直线轴对称,,,点与点对应,交于点,则线段的长为( )
A.5B.C.4D.
【答案】B
【分析】设,根据平行线性质和轴对称性质得到,再根据勾股定理得到关于线段、、的方程,解方程即可解决问题.
【详解】解:设,则,
∵,
∴;
∵与关于直线轴对称,
∴,
∴,
∴;
由勾股定理得:,
即,
解得:,
∴,
故选:B.
【点睛】本题主要考查了轴对称的性质,平行线的性质,勾股定理等知识点,根据勾股定理列出方程是解题的关键是.
7.(2021秋·山东济南·八年级统考期中)如图,三级台阶的每一级的长、宽、高分别为.点A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )dm.
A.12B.10C.17D.25
【答案】C
【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
【详解】解:三级台阶平面展开图为长方形,长为,宽为,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到B点最短路程为,
由勾股定理得:,
解得.
故选 C.
【点睛】本题主要考查了平面展开最短路径问题,掌握两点间线段最短是解答本题的关键.
8.(2022秋·八年级课时练习)如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2B.C.6D.8
【答案】D
【分析】设AD=DB=a,AF=CF=b,BE=CE=c,由勾股定理可求a2+b2=c2,由 ,可求b=4,即可求解.
【详解】解:设AD=DB=a,AF=CF=b,BE=CE=c,
∴ABa,ACb,BCc,
∵∠BAC=90°,
∴AB2+AC2=BC2,
∴2a2+2b2=2c2,
∴a2+b2=c2,
∵将等腰Rt△ADB和等腰Rt△AFC按如图方式叠放到等腰Rt△BEC,
∴BG=GH=a,
∵,
∴(a+c)(c﹣a)=16,
∴c2﹣a2=32,
∴b2=32,
∴b=4,
∴ACb=8,
故选:D.
【点睛】本题考查了勾股定理,折叠的性质,利用整体思想解决问题是本题的关键.
9.(2022春·甘肃庆阳·八年级校考期中)如图,一个梯子长2.5米,顶端靠在墙上,这时梯子下端与墙角距离为0.7米,梯子滑动后停在的位置上,测得长为0.8米,求梯子顶端下落了_________米.
【答案】0.4
【分析】在直角三角形ABC中,根据勾股定理得:AC=2.4米,由于梯子的长度不变,在直角三角形CDE中,根据勾股定理得CE=2米,进而得出答案.
【详解】解:在Rt△ABC中,AB=2.5米,BC=0.7米,
故AC=(米),
在Rt△ECD中,AB=DE=2.5米,CD=0.8+0.7=1.5(米),
故EC=(米),
故AE=ACCE=2.42=0.4(米).
答:梯子下滑了0.4米.
故答案为:0.4;
【点睛】此题考查了勾股定理的应用,此题中主要注意梯子的长度不变,分别运用勾股定理求得AC和CE的长,即可计算下滑的长度.
10.(2020秋·广东茂名·八年级校考阶段练习)如图,在一棵树的10米高B处有两只猴子,其中一只爬下树走向离树20米的池塘C,而另一只爬到树顶D后直扑池塘C,结果两只猴子经过的距离相等,这棵树有的高是______________ .
【答案】15米
【分析】根据题意确定已知线段的长,再根据勾股定理列方程进行计算.
【详解】设BD=米,则AD=()米,CD=()米,
∵,
∴,
解得.
即树的高度是10+5=15米.
故答案为:15米.
【点睛】本题主要考查了勾股定理的应用,把实际问题转化为数学模型,构造直角三角形,然后利用勾股定理解决.
11.(2022秋·山东济南·八年级济南市章丘区第四中学校考阶段练习)如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
【答案】6或7或12或14
【分析】当OP=OD时,可得P1点;当DP=OD时,可得P2、P3、P4三种情况,再运用勾股定理可分别求解.
【详解】解:当OP=OD时,可得P1点,此时由勾股定理可得,OC2+CP12=OP12,即42+CP12=52,解得CP1=3,则t=秒;
当DP=OD时,可得P2、P3、P4三种情况,当P点运动到P2位置时,作P2M2⊥OA,由勾股定理可得,P2M22+ DM22=DP22,即42+ DM22=52,解得DM2=3,同理可解得DM3=AP4=3,
故,当P点运动到P2位置时,t=秒;当P点运动到P3位置时,t=秒;当P点运动到P4位置时,t=秒;
故答案为6或7或12或14.
【点睛】本题有些难度,难点在于一共有4种情况,也可采取画圆法确定P点可能的位置,即以O点为圆心、5为半径画圆,或者以D点为圆心、5为半径画圆,从而确定P点可能位置.
12.(2022秋·八年级课时练习)将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值__,h的最大值__.
【答案】 11cm 12cm
【分析】根据筷子的摆放方式得到:当筷子与杯底垂直时h最大,当筷子与杯底及杯高构成直角三角形时h最小,利用勾股定理计算即可.
【详解】解:当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
此时,在杯子内的长度==13(cm),
故h=24﹣13=11(cm).
故h的取值范围是11≤h≤12cm.
故答案为:11cm;12cm.
【点睛】此题考查勾股定理的实际应用,正确理解题意、掌握勾股定理的计算公式是解题的关键.
13.(2022秋·全国·八年级专题练习)如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点160米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心,100米为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为36千米/时,则对学校A的噪声影响最大时卡车P与学校A的距离是___米;重型运输卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间是____秒.
【答案】 80 12
【分析】作于,求出的长即可解决问题,如图以为圆心m为半径画圆,交于、两点,求出的长,利用时间计算即可.
【详解】解:作于,
,m,
m,
即对学校的噪声影响最大时卡车与学校的距离m.
如图以为圆心m为半径画圆,交于、两点,
,
,
在中,m,
m,
重型运输卡车的速度为36千米时米秒,
重型运输卡车经过的时间(秒,
故卡车沿道路方向行驶一次给学校带来噪声影响的时间为12秒.
故答案为:80,12.
【点睛】本题考查勾股定理的应用、解直角三角形的应用,解题的关键是理解题意,学会添加常用辅助线构造直角三角形解决问题,属于中考常考题型.
14.(2021春·四川成都·八年级校考期中)在等腰直角三角形中,,,是边上一点,且,是边上一点,将沿翻折,使点落在线段的点上,则_________.
【答案】##
【分析】过F点作于M点,易得,根据折叠的性质有:,,,即有,,再证明,即在中,可得,,即有,,在中,,可得,在中,,可得,问题随之得解.
【详解】过F点作于M点,如图,
∵在等腰直角三角形中,,,
∴,
∵,
∴,
根据折叠的性质有:,,,
∴,,
∵,,
∴,
∵在中,,,
∴,,
∴,,
∴,
∵,,
∴,即,
∴,
∵在中,,
∴,
∵,
∴在中,,
∴,
∴,
故答案为:.
【点睛】本题主要考查了折叠的性质,勾股定理,等腰三角形的判定与性质性质,含角的直角三角形的性质等知识,掌握折叠的性质,并求出,是解答本题的关键.
15.(2021秋·广东佛山·八年级统考阶段练习)如图,一个梯子AB,顶端A靠在墙AC上,这是梯子的顶端距地面的垂直高度为24米,若梯子的顶端下滑4米,底端将水平滑动了8米,求滑动前梯子底端与墙的距离CB是多少?
【答案】7米
【分析】设BC=xm,则CD=(x+8)m,利用勾股定理分别表示出、,∵AB=ED,∴,求出x的值即可完成.
【详解】解:根据题意,AC=24m,AE=4m,BD=8m,则EC=20m
设BC=xm,则CD=(x+8)m
在中,由勾股定理得,
在中,由勾股定理得,
∵AB=ED
∴
解得:
滑动前梯子底端与墙的距离CB是7米.
【点睛】本题考查勾股定理的应用,难度较低,灵活运用勾股定理是解题关键.
16.(2022春·四川泸州·八年级统考阶段练习)如图,四边形为某街心公园的平面图,经测量米,米,且.
(1)求的度数;
(2)若为公园的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点处安装一个监控装置来监控道路的车辆通行情况,已知摄像头能监控的最大范围为周围的100米(包含100米),求被监控到的道路长度为多少?
【答案】(1)135°;(2)被监控到的道路长度为米.
【分析】(1)易得∠CAB=45°,由勾股定理求出AC的长度,然后由勾股定理的逆定理,得到△ACD是直角三角形,则∠CAD=90°,即可得到答案;
(2)过点D作DE⊥AB,然后作点A关于DE的对称点F,连接DF,由轴对称的性质,得到DF=DA=100,则只要求出AF的长度,即可得到答案.
【详解】解:(1)∵,,
∴△ABC是等腰直角三角形,
∴,∠CAB=45°,
∵,
在△ACD中,有
,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴;
(2)过点D作DE⊥AB,然后作点A关于DE的对称点F,连接DF,如图:
由轴对称的性质,得DF=DA=100,AE=EF,
由(1)知,∠BAD=135°,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,即AE=DE,
在Rt△ADE中,有,
解得:,
∴;
∴被监控到的道路长度为米.
【点睛】本题考查了轴对称的性质,等腰直角三角形的判定和性质,勾股定理,以及勾股定理的逆定理,解题的关键是熟练掌握所学的知识,正确利用轴对称的性质和勾股定理求出所需边的长度,从而进行计算.
17.(2022秋·江苏宿迁·八年级统考期中)如图1,直线,垂足为O,直线l分别与射线、相交于点A、B,且,,连接.
(1)求线段的长;
(2)若点C为直线l上的一个动点,求点O到点C的距离的最小值;
(3)如图2,将沿直线l折叠,点O落在点D处,,垂足为点E,求的长;
(4)若点F为直线或上的一个动点,使得以A、B、F为顶点的三角形是等腰三角形,则满足条件的所有点F的个数为______个.
【答案】(1)
(2)点O到点C的距离的最小值为
(3)
(4)8
【分析】(1)根据勾股定理直接求解即可;
(2)过点O作于点C,此时最小,根据等积法求出即可;
(3)连接,交于点C,根据对称性求出:,,设,则,根据勾股定理列出关于x的方程,解方程即可得到x的值,最后根据勾股定理求出结果即可;
(4)分类进行讨论得出结果即可.
【详解】(1)解:∵,
∴,
∵,,
∴.
(2)解:过点O作于点C,此时最小,如图所示:
∵,
∴,
即点O到点C的距离的最小值为.
(3)解:连接,交于点C,如图所示:
∵点O与点D关于对称,
∴垂直平分,
即,,
∴,
∴,
根据折叠可知,,
设,则,
在中,,
在中,
∴,
解得:,
∴.
(4)解:当,点F在上时,如图所示:
当,点F在上时,如图所示:
当,点F在上时,如图所示:
当,点F在上时,如图所示:
当,点F在上时,如图所示:
当,点F在上时,如图所示:
综上分析可知,满足条件的所有点F的个数为8个.
故答案为:8.
【点睛】本题主要考查了勾股定理,等腰三角形的定义,轴对称的性质,解题的关键是注意进行分类讨论.
18.(2022秋·陕西西安·八年级校考阶段练习)如图1,在中,,,,点为边上一动点,将沿直线折叠,得到,请解决下列问题.
(1)______;当点恰好落在斜边上时,______;
(2)连接,当是以为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点到直线的距离;
(3)如图3,为边上一点,且,连接,当为直角三角形时,______.(请写出所有满足条件的长)
【答案】(1),
(2)图见解析,到直线的距离为
(3)或或
【分析】(1)直接根据勾股定理可得的长度,画出点恰好落在斜边上时的图形,然后根据三角形面积的不同表达方式可得的长,则结果可得;
(2)当点与点重合时,是以为底边的等腰三角形,过点作于点,设与交于点,然后根据三角形的面积,折叠的性质以及勾股定理进行解答即可;
(3)分三种情况:当;当;当;画出相应图形分别进行求解即可.
(1)
解:根据勾股定理得:,
当点恰好落在斜边上时,如图:
根据折叠的性质可知,
则,
解得:,
故答案为:,;
(2)
如图,当点与点重合时,是以为底边的等腰三角形,
过点作于点,设与交于点,
将沿直线折叠,得到,
,
,
,
在中,,
,
解得:,
点到直线的距离为;
(3)
当时,如图:
,
为等腰直角三角形,
;
当时,如图:
,,
在中,,
,
,
解得:;
当时,如图:
过点作于点,
,
在中,,
,
设,则,
在中,,
即,
解得,
,
综上所述,的长为或或,
故答案为:或或.
【点睛】本题考查了勾股定理,折叠的性质,等腰三角形的性质等知识点,能够根据题意画出相应的图形是解本题的关键.
19.(2023春·全国·八年级专题练习)如图,点是等腰直角的直角边上的一点,AE的中垂线分别交,,于点,,,且.
(1)求的度数.
(2)若,求的长.
(3)若平分,则:
①判断线段与的位置关系并证明.
②求出的长.
【答案】(1);(2);(3)①,证明见解析;②
【分析】(1)利用线段垂直平分线的性质得到AD=DE,AF=EF,继而得到∠DAE=∠DEA,∠FAE=∠FEA,再根据即可得到;
(2)在Rt△BDE中,根据勾股定理可得BD2+BE2=DE2,继而根据AD+BD=AB=2,AD=DE,继而得到关于AD的方程,解方程即可得;
(3)①利用平分,得到,根据为等腰三角形得到,求出,,由推出,得到结论;
②在Rt△BDE中,由勾股定理可得BD2+BE2=DE2,再根据BD=BE,AD=DE即可得出关于BE的方程,求解即可.
【详解】(1)∵为的中垂线,
∴AD=DE,AF=EF,
∴∠DAE=∠DEA,∠FAE=∠FEA,
∴∠DEF=∠DEA+∠FEA=∠DAE+∠FAE=∠BAC,
∴和为等腰三角形.
又∵为等腰直角三角形,∠B=90°,
∴,
∴;
(2)∵在Rt△BDE中,∠B=90°,
∴BD2+BE2=DE2,
∵AD+BD=AB=2,,AD=DE,
∴(2-AD)2+=AD2,
∴;
(3)①∵平分,∠BAC=45°,
∴,
∵AD=DE,
∴∠AED=∠DAE=22.5°,
∴∠BDE=∠DAE+∠DEA=45°,
∵∠B=90°,
∴∠BED=90°-45°=45°,
又,
∴∠BEF=∠BED+∠DEF=90°,
∴.
②∵在Rt△BDE中,∠B=90°,∠BDE=∠BED=45°,
∴BD=BE,BD2+BE2=DE2,
∴DE=,
∵AD=DE,AD+BD=AB=2,
∴,
∴.
【点睛】此题考查等腰直角三角形的性质,线段垂直平分线的性质,折叠的性质,勾股定理等,综合了三角形的多处知识点,熟练掌握和灵活运用相关知识是解题的关键.
20.(2021秋·江苏无锡·八年级校联考期中)如图1,在长方形中,BC=3,动点从出发,以每秒1个单位的速度,沿射线方向移动,作关于直线的对称,设点的运动时间为
(1)当P点在线段BC上且不与C点重合时,若直线PB’与直线CD相交于点M,且∠PAM=45°,试求:AB的长
(2)若AB=4
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
【答案】(1)AB的长为3;(2)①;②t的值为或或4.
【分析】(1)如图所示,延长与CD交于M,连接AM,用角角边证明,可推出AB=BC=3.
(2)①在Rt△中,找出边长利用勾股定理建立方程求解;
②分三种情况讨论:,,,分别作出相应的图形,在中,分别找出边长,利用勾股定理建立方程求解.
【详解】(1)如图所示,延长与CD交于M,连接AM,
由折叠的性质可知,,
∵,,
∴
在和中,
∴≌(AAS)
∴
又∵ABCD为矩形,∴AD=BC=3,
∴AB=3
(2)①在Rt△ABC中,
∵点P点的运动时间为t,速度为1,∴BP=t,
,,,
在Rt△中,由勾股定理有,即,解得.
②当,如下图所示,
∵四边形ABCD为矩形,∴AD=BC=3,CD=AB=4,
有折叠性质有,在Rt△中,
,
∴
在Rt△中,,
,即,解得
当∠=90°时,如下图所示,
由折叠可得,
在Rt△中,
在Rt△中,,,
,即,解得
当=90°时,如下图所示,根据折叠易得四边形为正方形,∴PB=AB=4
综上,满足题意的t的值为或或4.
【点睛】本题考查折叠问题里勾股定理的应用,关键是根据折叠的性质找出边长,利用勾股定理建立方程.
人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(四)之压轴满分题型专训(原卷版+解析): 这是一份人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(四)之压轴满分题型专训(原卷版+解析),共131页。
人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(二)之基础常考题型专训(原卷版+解析): 这是一份人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(二)之基础常考题型专训(原卷版+解析),共111页。
人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(三)之易错必刷题型专训(原卷版+解析): 这是一份人教版八年级数学下册重难点专题提升精讲精练期末重难点特训(三)之易错必刷题型专训(原卷版+解析),共106页。












