人教A版高一数学上学期期中期末必考题型归纳及过关测试专题17三角函数的性质(原卷版+解析)

这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题17三角函数的性质(原卷版+解析)，共32页。
1、正弦函数、余弦函数的图象
（1）正弦函数的图象．
= 1 \* GB3 ①画点
在直角坐标系中画出以原点为圆心的单位圆，与轴正半轴的交点为．在单位圆上，将点绕着点旋转弧度至点，根据正弦函数的定义，点的纵坐标．由此，以为横坐标，为纵坐标画点，即得到函数图象上的点．
= 2 \* GB3 ②画（）的图象
把轴上从到这一段分成等份，使的值分别为，，，，…，，它们所对应的角的终边与单位圆的交点将圆周等份，再按上述画点的方法，就可画出自变量取这些值时对应的函数图象上的点．然后将这些点用光滑的曲线连接起来，即得（）的图象．
= 3 \* GB3 ③（）的图象
由诱导公式一可知，函数，，且的图象，与函数，的图象形状完全一样．因此将函数，的图象不断向左、向右平行移动（每次个单位长度），就可以得到正弦函数，的图象（如下图）．
正弦函数的图象叫做正弦曲线．
= 4 \* GB3 ④五点作图法
在函数，的图象上，有以下五个关键点：
，，，，．
画出这五个关键点，然后用光滑的曲线将它们连接起来，可得到正弦函数的简图．这种作图的方法称为”五点作图法”．
（2）余弦函数的图象
因为，所以可将正弦函数，的图象向左平移个单位长度即得余弦函数，的图象．
余弦函数，的图象叫做余弦曲线．
余弦函数，的图象上五个关键点是：，，，，．
2、正弦函数、余弦函数的性质
（1）周期性
一般地，对于函数，如果存在一个非零常数，使得当取定义域内的每一个值时，都有
，
那么函数就叫做周期函数．非零常数叫做这个函数的周期．
如果在周期函数的所有周期中存在一个最小的正数，那么这个最小正数就叫做的最小正周期．
正弦函数是周期函数，（且）都是它的周期，最小正周期是．
余弦函数也是周期函数，（且）都是它的周期，最小正周期是．
（2）奇偶性
正弦函数是奇函数，余弦函数是偶函数．
（3）单调性
正弦函数，在每一个闭区间（）上都单调递增，其值从增大到；在每一个闭区间（）上都单调递减，其值从减小到．
余弦函数，在每一个闭区间（）上都单调递增，其值从增大到；在每一个闭区间（）上都单调递减，其值从减小到．
（4）最大值与最小值
正弦函数当且仅当（）时取得最大值，当且仅当（）时取得最小值．
余弦函数当且仅当（）时取得最大值，当且仅当（）时取得最小值．
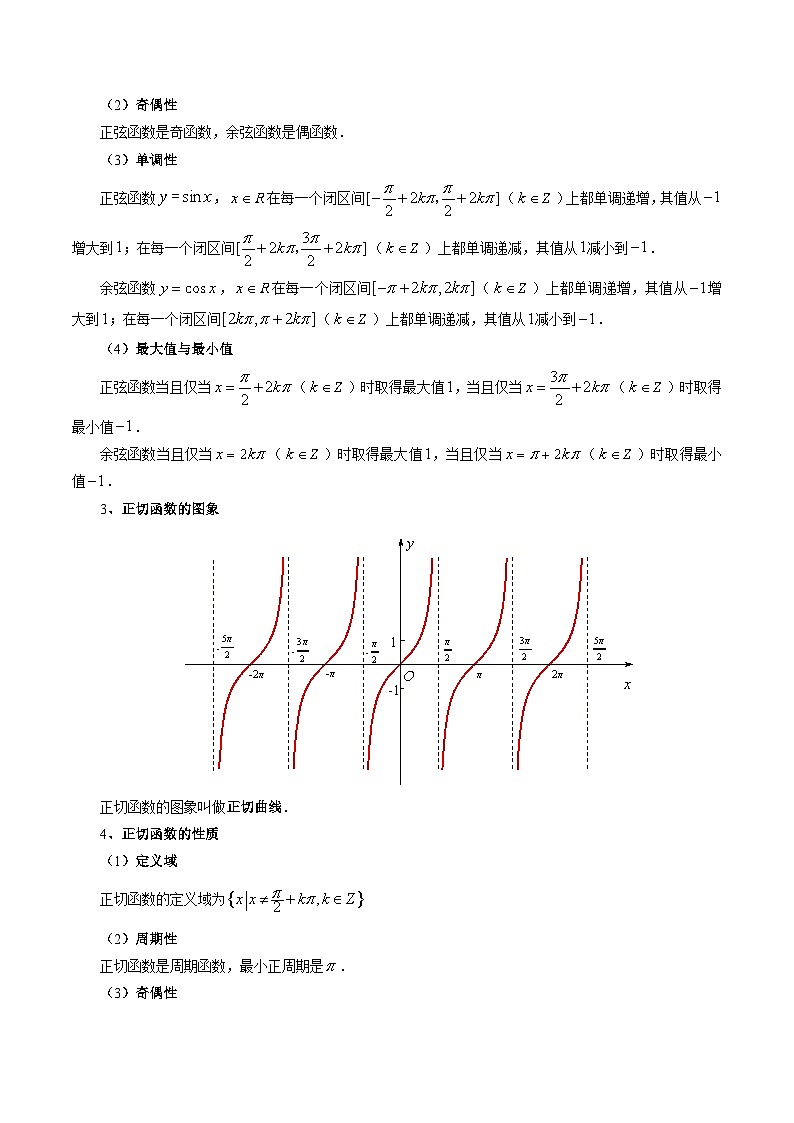
3、正切函数的图象
正切函数的图象叫做正切曲线．
4、正切函数的性质
（1）定义域
正切函数的定义域为
（2）周期性
正切函数是周期函数，最小正周期是．
（3）奇偶性
正切函数是奇函数．
（4）单调性
正切函数在每一个开区间（）上都单调递增．
（5）值域
正切函数的值域是实数集．
【典型例题】
例1．(2023·江西省万载中学高一期中）已知函数，，
(1)求函数的单调递减区间；
(2)求函数的最大值、最小值及对应的x值的集合；
(3)若对任意，存在，使得，求实数m的取值范围.
例2．(2023·新疆·柯坪湖州国庆中学高一期末）已知函数，.
(1)求的最小正周期；
(2) 有零点，求的范围.
例3．(2023·北京·高一期末）已知函数.
(1)请用五点法做出一个周期内的图像；
(2)若函数在区间上有两个零点，请写出的取值范围，无需说明理由.
例4．(2023·浙江省杭州第九中学高一期末）某同学用“五点法”作函数（，，）在某一个周期内的图象时，列表并填入了部分数据，见下表：
(1)根据上表数据，直接写出函数的解析式，并求函数的最小正周期和在上的单调递减区间.
(2)求在区间上的最大值和最小值.
例5．(2023·西藏拉萨·高一期末）已知函数（，），再从条件①、条件②、条件③这三个条件中选择两个作为一组已知条件，使的解析式唯一确定．
条件①：的最小正周期为；
条件②：为奇函数；
条件③：图象的一条对称轴为．
(1)求的解析式；
(2)设函数，求在区间上的最大值．
注：如果选择多组条件分别解答，按第一个解答计分．
例6．(2023·安徽·砀山中学高一期中）已知函数（，），其图象一条对称轴与相邻对称中心的横坐标相差，______；从以下两个条件中任选一个补充在空白横线中．
①函数向左平移个单位得到的图象关于轴对称且．
②函数的一条对称轴为且；
(1)求函数的解析式；
(2)若，方程存在4个不相等的实数根，求实数的取值范围．
【过关测试】
一、单选题
1．(2023·上海市控江中学高一期末）已知常数，函数在区间上是严格增函数，则实数的取值范围是（ ）
A．B．
C．D．
2．(2023·上海·格致中学高一期中）函数的一个对称中心是（ ）
A．B．C．D．
3．(2023·浙江·高一期末）函数为增函数的区间是（ ）
A．B．C．D．
4．(2023·湖南·武冈市教育科学研究所高一期末）关于函数图象的对称性，下列说法正确的是（ ）
A．关于直线对称B．关于直线对称
C．关于点对称D．关于点对称
5．(2023·全国·高一课时练习）若函数在区间内存在最小值，则的值可以是（ ）
A．B．C．D．
6．(2023·全国·高一课时练习）已知函数，则（ ）
A．的最大值为3，最小值为1
B．的最大值为3，最小值为-1
C．的最大值为，最小值为
D．的最大值为，最小值为
7．(2023·全国·高一课时练习）已知函数的图象在区间上恰有3个最高点，则的取值范围为（ ）
A．B．
C．D．
8．(2023·北京·高一期末）记函数的最小正周期为，若，为的零点，则的最大值为（ ）
A．B．C．D．
二、多选题
9．(2023·全国·高一课时练习）已知直线是函数图象的一条对称轴，则（ ）
A．是偶函数B．是图象的一条对称轴
C．在上单调递减D．当时，函数取得最小值
10．(2023·安徽·砀山中学高一期中）已知函数（）在上单调，则的可能值为（ ）
A．2B．3C．4D．5
11．(2023·安徽省宿州市苐三中学高一期中）已知函数，则下列结论正确的有（ ）
A．
B．函数图像关于直线对称
C．函数的值域为
D．若函数有四个零点，则实数的取值范围是
12．(2023·全国·高一课时练习）关于函数，的图象与直线（为常数）的交点情况，下列说法正确的是（ ）
A．当或时，有0个交点B．当或时，有1个交点
C．当时，有2个交点D．当时，有2个交点
三、填空题
13．(2023·上海市曹杨中学高一期末）已知函数，若存在，有，则的最小值为______．
14．(2023·全国·高一课时练习）写出一个同时具有下列性质①②的函数______．（注：不是常函数）
①；②．
15．(2023·全国·高一课时练习）函数的值域为_____________．
16．(2023·全国·高一课时练习）设函数若在区间上单调，且，则的最小正周期为____．
四、解答题
17．(2023·上海市金汇高级中学高一期末）函数的部分图象如图所示．
(1)写出的最小正周期及图中、的值；
(2)求在区间上的最大值和最小值．
18．(2023·江苏盐城·高一期末）设.
(1)若函数的最大值是最小值的3倍，求b的值；
(2)当时，函数正零点由小到大依次为x1，x2，x3，…，若，求ω的值.
19．(2023·全国·高一课时练习）已知下列三个条件：①函数为奇函数；②当时，；③是函数的一个零点．从这三个条件中任选一个填在下面的横线处，并解答下列问题．
已知函数，______．
(1)求函数的解析式；
(2)求函数在上的单调递增区间．
20．(2023·山东东营·高一期中）函数的最小值为，
(1)当时，求；
(2)若，求实数
21．(2023·甘肃兰州·高一期中）已知点、是函数图象上的任意两点，角的终边经过点，当时，的最小值为．
(1)求函数的解析式；
(2)求函数的单调区间．
22．(2023·湖北·华中师大一附中高一期末）已知函数．
(1)求函数的单调递增区间；
(2)若函数在区间上有且仅有两个零点，求实数k的取值范围．
0
0
0
专题17 三角函数的性质
【考点预测】
1、正弦函数、余弦函数的图象
（1）正弦函数的图象．
= 1 \* GB3 ①画点
在直角坐标系中画出以原点为圆心的单位圆，与轴正半轴的交点为．在单位圆上，将点绕着点旋转弧度至点，根据正弦函数的定义，点的纵坐标．由此，以为横坐标，为纵坐标画点，即得到函数图象上的点．
= 2 \* GB3 ②画（）的图象
把轴上从到这一段分成等份，使的值分别为，，，，…，，它们所对应的角的终边与单位圆的交点将圆周等份，再按上述画点的方法，就可画出自变量取这些值时对应的函数图象上的点．然后将这些点用光滑的曲线连接起来，即得（）的图象．
= 3 \* GB3 ③（）的图象
由诱导公式一可知，函数，，且的图象，与函数，的图象形状完全一样．因此将函数，的图象不断向左、向右平行移动（每次个单位长度），就可以得到正弦函数，的图象（如下图）．
正弦函数的图象叫做正弦曲线．
= 4 \* GB3 ④五点作图法
在函数，的图象上，有以下五个关键点：
，，，，．
画出这五个关键点，然后用光滑的曲线将它们连接起来，可得到正弦函数的简图．这种作图的方法称为”五点作图法”．
（2）余弦函数的图象
因为，所以可将正弦函数，的图象向左平移个单位长度即得余弦函数，的图象．
余弦函数，的图象叫做余弦曲线．
余弦函数，的图象上五个关键点是：，，，，．
2、正弦函数、余弦函数的性质
（1）周期性
一般地，对于函数，如果存在一个非零常数，使得当取定义域内的每一个值时，都有
，
那么函数就叫做周期函数．非零常数叫做这个函数的周期．
如果在周期函数的所有周期中存在一个最小的正数，那么这个最小正数就叫做的最小正周期．
正弦函数是周期函数，（且）都是它的周期，最小正周期是．
余弦函数也是周期函数，（且）都是它的周期，最小正周期是．
（2）奇偶性
正弦函数是奇函数，余弦函数是偶函数．
（3）单调性
正弦函数，在每一个闭区间（）上都单调递增，其值从增大到；在每一个闭区间（）上都单调递减，其值从减小到．
余弦函数，在每一个闭区间（）上都单调递增，其值从增大到；在每一个闭区间（）上都单调递减，其值从减小到．
（4）最大值与最小值
正弦函数当且仅当（）时取得最大值，当且仅当（）时取得最小值．
余弦函数当且仅当（）时取得最大值，当且仅当（）时取得最小值．
3、正切函数的图象
正切函数的图象叫做正切曲线．
4、正切函数的性质
（1）定义域
正切函数的定义域为
（2）周期性
正切函数是周期函数，最小正周期是．
（3）奇偶性
正切函数是奇函数．
（4）单调性
正切函数在每一个开区间（）上都单调递增．
（5）值域
正切函数的值域是实数集．
【典型例题】
例1．(2023·江西省万载中学高一期中）已知函数，，
(1)求函数的单调递减区间；
(2)求函数的最大值、最小值及对应的x值的集合；
(3)若对任意，存在，使得，求实数m的取值范围.
【解析】（1），解不等式得： ，
所以函数的单调递减区间为.
（2），即时， ，
，即 时，；
（3）时，，，
时， ， ，
要使得，只需， .
例2．(2023·新疆·柯坪湖州国庆中学高一期末）已知函数，.
(1)求的最小正周期；
(2) 有零点，求的范围.
【解析】（1）由于，故其最小正周期为；
（2）因为 有零点，
故有解，
即有解，
因为，所以，
故.
例3．(2023·北京·高一期末）已知函数.
(1)请用五点法做出一个周期内的图像；
(2)若函数在区间上有两个零点，请写出的取值范围，无需说明理由.
【解析】（1）列表
（2）的取值范围是.
例4．(2023·浙江省杭州第九中学高一期末）某同学用“五点法”作函数（，，）在某一个周期内的图象时，列表并填入了部分数据，见下表：
(1)根据上表数据，直接写出函数的解析式，并求函数的最小正周期和在上的单调递减区间.
(2)求在区间上的最大值和最小值.
【解析】（1）根据五点法的表格，所以
所以的最小正周期
令，
解之得
又，所以或
即在上的单调递减区间为，
（2）由于
所以
所以
所以
当即时，函数的最小值为;
当即时，函数的最大值为.
例5．(2023·西藏拉萨·高一期末）已知函数（，），再从条件①、条件②、条件③这三个条件中选择两个作为一组已知条件，使的解析式唯一确定．
条件①：的最小正周期为；
条件②：为奇函数；
条件③：图象的一条对称轴为．
(1)求的解析式；
(2)设函数，求在区间上的最大值．
注：如果选择多组条件分别解答，按第一个解答计分．
【解析】（1）选择①②：
由条件①即已知，可得，所以，
由条件②得，所以，即，解得，
因为，所以，所以，
经验证，符合题意；
选择条件①③：
由条件①即已知，可得，所以，
由条件③得，解得，
因为，所以，所以，
选择条件：②③：
由条件②得，所以，即，解得，
因为，所以，所以，
由条件③得，解得，此时不唯一，不符合题意.
（2）由函数
，
因为，所以，
所以当，即时，函数取得最大值，最大值为.
例6．(2023·安徽·砀山中学高一期中）已知函数（，），其图象一条对称轴与相邻对称中心的横坐标相差，______；从以下两个条件中任选一个补充在空白横线中．
①函数向左平移个单位得到的图象关于轴对称且．
②函数的一条对称轴为且；
(1)求函数的解析式；
(2)若，方程存在4个不相等的实数根，求实数的取值范围．
【解析】(1)由题意可知，函数的最小正周期为，∴．
选①，将函数向左平移个单位，所得函数为.
由于函数的图象关于轴对称，可得（），解得（）.
∵，所以，的可能取值为、．
若，则，，符合题意；
若，则，，不符合题意．
所以，；
选②：因为函数的一条对称轴，则（），
解得（）.
∵，所以，的可能取值为、．
若，则，则，符合题意；
若，则，则，不符合题意．
所以，；
(2)令，由得，，
所以．其中满足，时为增函数，满足时为减函数
解方程得：，
要使方程存在4个不相等的实数根，
当，即在上存在两解，
故取值范围应在或在或．
即或或
解得：或或
故所求的的取值范围是
【过关测试】
一、单选题
1．(2023·上海市控江中学高一期末）已知常数，函数在区间上是严格增函数，则实数的取值范围是（ ）
A．B．
C．D．
答案：B
【解析】，
由于且在区间上是严格增函数，
所以，
即的取值范围是.
故选：B
2．(2023·上海·格致中学高一期中）函数的一个对称中心是（ ）
A．B．C．D．
答案：C
【解析】令，
解得，
所以函数图象的对称中心是，
令,得函数图像的一个对称中心是，
故选：C.
3．(2023·浙江·高一期末）函数为增函数的区间是（ ）
A．B．C．D．
答案：C
【解析】，
，，，
令可的的递增区间为.
故选：C
4．(2023·湖南·武冈市教育科学研究所高一期末）关于函数图象的对称性，下列说法正确的是（ ）
A．关于直线对称B．关于直线对称
C．关于点对称D．关于点对称
答案：D
【解析】对A，，，故A错误；
对B，，，故B错误；
对C，，，故C错误；
对D，，此时，故D正确，
故选：D
5．(2023·全国·高一课时练习）若函数在区间内存在最小值，则的值可以是（ ）
A．B．C．D．
答案：B
【解析】由，得.
若在开区间内存在最小值，则，
解得，
故选:B.
6．(2023·全国·高一课时练习）已知函数，则（ ）
A．的最大值为3，最小值为1
B．的最大值为3，最小值为-1
C．的最大值为，最小值为
D．的最大值为，最小值为
答案：C
【解析】因为函数，
设，，
则，
所以，，
当时，；当时，.
故选：C
7．(2023·全国·高一课时练习）已知函数的图象在区间上恰有3个最高点，则的取值范围为（ ）
A．B．
C．D．
答案：C
【解析】由题意，函数，
因为，可得，
又函数的图象在区间上恰有3个最高点，
所以，解得，
即实数的取值范围是．
故选：C．
8．(2023·北京·高一期末）记函数的最小正周期为，若，为的零点，则的最大值为（ ）
A．B．C．D．
答案：B
【解析】因为
所以最小正周期，
因为，
又，
所以，
即，
又为的零点，
所以，解得，
因为，
所以当时，
所以的最大值为，
故选：B
二、多选题
9．(2023·全国·高一课时练习）已知直线是函数图象的一条对称轴，则（ ）
A．是偶函数B．是图象的一条对称轴
C．在上单调递减D．当时，函数取得最小值
答案：AC
【解析】因为直线是函数图象的一条对称轴，
所以，，
又，所以，所以．
，是偶函数，故A正确；
令，解得:，
所以图象的对称轴方程为，而不能满足上式，故B错误；
当时，，此时函数单调递减，故C正确；
显然函数的最小值为，当时，，故D错误．
故选：AC．
10．(2023·安徽·砀山中学高一期中）已知函数（）在上单调，则的可能值为（ ）
A．2B．3C．4D．5
答案：AB
【解析】因为，故可得，
又的单调增区间为，
故，
解得且
又，故，.
故选：AB.
11．(2023·安徽省宿州市苐三中学高一期中）已知函数，则下列结论正确的有（ ）
A．
B．函数图像关于直线对称
C．函数的值域为
D．若函数有四个零点，则实数的取值范围是
答案：AC
【解析】因为，
所以，故A正确；
由题可知函数的定义域为，不关于对称，故B错误；
当时，，
当时，，，
所以函数的值域为，故C正确；
由可得，则函数与有四个交点，
作出函数与的大致图象，
由图象可知函数有四个零点，则实数的取值范围是，故D错误.
故选：AC.
12．(2023·全国·高一课时练习）关于函数，的图象与直线（为常数）的交点情况，下列说法正确的是（ ）
A．当或时，有0个交点B．当或时，有1个交点
C．当时，有2个交点D．当时，有2个交点
答案：AB
【解析】根据函数的解析式作出函数的图象如图所示,
对于选项A，当或时，有0个交点，故A正确；
对于选项B，当或时，有1个交点，故B正确；
对于选项C，当时，只有1个交点，故C错误；
对于选项D，当时，只有1个交点，故D错误．
故选:AB．
三、填空题
13．(2023·上海市曹杨中学高一期末）已知函数，若存在，有，则的最小值为______．
答案：
【解析】∵的周期，由得.
故答案为：.
14．(2023·全国·高一课时练习）写出一个同时具有下列性质①②的函数______．（注：不是常函数）
①；②．
答案：（答案不唯一）
【解析】由知函数的一个周期是，则满足条件②．
∵，∴满足条件①．
故答案为：（答案不唯一）
15．(2023·全国·高一课时练习）函数的值域为_____________．
答案：
【解析】令，，
则，即，
所以，
又因为，所以，
即函数的值域为．
故答案为：.
16．(2023·全国·高一课时练习）设函数若在区间上单调，且，则的最小正周期为____．
答案：
【解析】函数，，，若在区间上单调，
则，．
，为的一条对称轴，
且即为的一个对称中心，
只有当时，解得，，
故答案为:
四、解答题
17．(2023·上海市金汇高级中学高一期末）函数的部分图象如图所示．
(1)写出的最小正周期及图中、的值；
(2)求在区间上的最大值和最小值．
【解析】（1）,
令，，
解得：，由图可知，当时，，此时函数取得最大值；
（2）当时，，
此时
所以函数的最大值是3，最小值是
18．(2023·江苏盐城·高一期末）设.
(1)若函数的最大值是最小值的3倍，求b的值；
(2)当时，函数正零点由小到大依次为x1，x2，x3，…，若，求ω的值.
【解析】(1)由题设，可得.
(2)令，则，
所以或且，
则或且，
由且正零点由小到大依次为x1，x2，x3，…，
所以、、，则，
所以.
19．(2023·全国·高一课时练习）已知下列三个条件：①函数为奇函数；②当时，；③是函数的一个零点．从这三个条件中任选一个填在下面的横线处，并解答下列问题．
已知函数，______．
(1)求函数的解析式；
(2)求函数在上的单调递增区间．
【解析】（1）选择条件①．
∵为奇函数，
∴，解得，．
∵，∴，∴；
选条件②．
，∴，
∴，或，，
∵，∴，∴
选条件③．
（1）∵是函数的一个零点，
∴，∴，．
∵，∴，∴.
（2）由，，得，，
令，得，令，得，
∴函数在上的单调递增区间为，．
20．(2023·山东东营·高一期中）函数的最小值为，
(1)当时，求；
(2)若，求实数
【解析】（1）当时，
.
所以，当时，取得最小值，即.
（2）
，
若，即时，则当时，有最小值，.
若，即时，则当时，有最小值，.
所以，
若，得或
由解得或（舍去），
由解得（舍去）.
所以
21．(2023·甘肃兰州·高一期中）已知点、是函数图象上的任意两点，角的终边经过点，当时，的最小值为．
(1)求函数的解析式；
(2)求函数的单调区间．
【解析】(1)角的终边经过点，所以，，，，
因为，，由当时，的最小值为，
所以，函数的最小正周期为，，则.
(2)由可得，
所以，函数的减区间为，
由可得，
所以，函数的增区间为.
22．(2023·湖北·华中师大一附中高一期末）已知函数．
(1)求函数的单调递增区间；
(2)若函数在区间上有且仅有两个零点，求实数k的取值范围．
【解析】（1）
，
令，所以，
所以函数的单调递增区间为：
（2）函数在区间上有且仅有两个零点，即曲线与直线在区间上有且仅有两个交点，由，当时，，设，则，且，
若要使曲线与直线区间上有且仅有两个交点，
则.
0
0
1
0
0
0
0
0