

所属成套资源:人教A版高一数学上学期期中期末必考题型归纳及过关测试(原卷版+解析)
人教A版高一数学上学期期中期末必考题型归纳及过关测试专题13指数函数及其性质(原卷版+解析)
展开
这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题13指数函数及其性质(原卷版+解析),共28页。
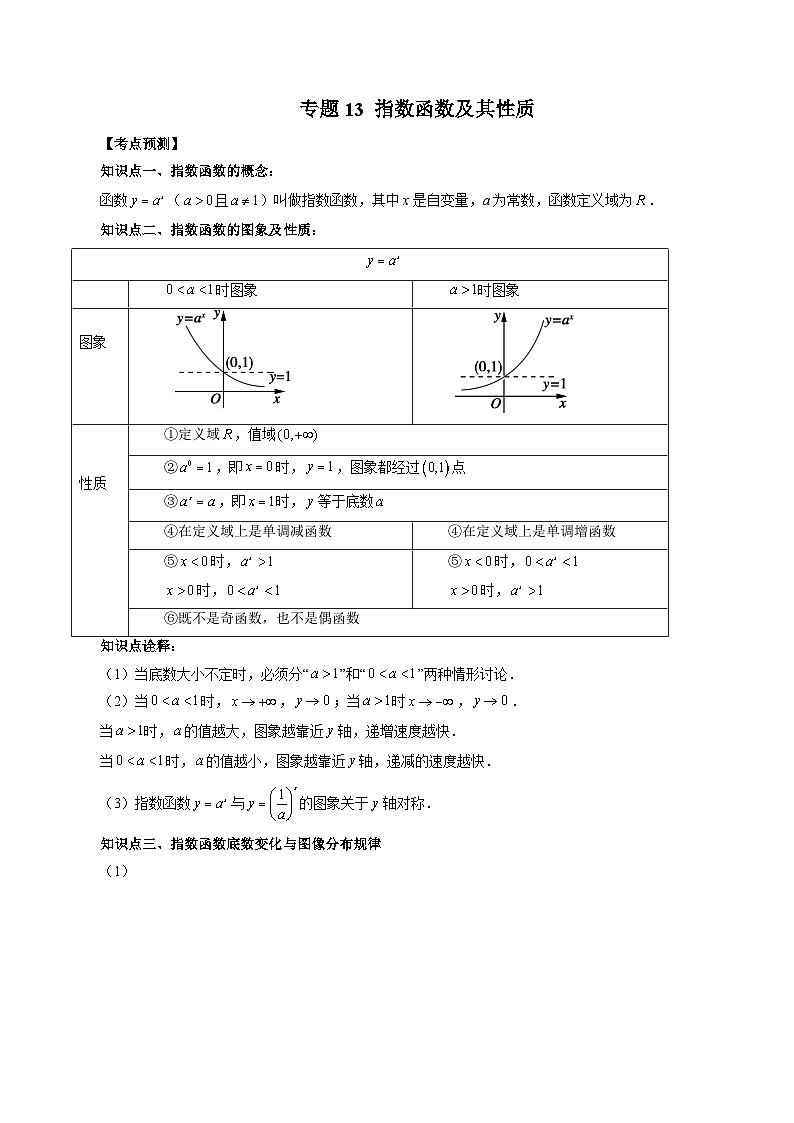
知识点一、指数函数的概念:
函数(且)叫做指数函数,其中x是自变量,a为常数,函数定义域为.
知识点二、指数函数的图象及性质:
知识点诠释:
(1)当底数大小不定时,必须分“”和“”两种情形讨论.
(2)当时,,;当时,.
当时,的值越大,图象越靠近轴,递增速度越快.
当时,的值越小,图象越靠近轴,递减的速度越快.
(3)指数函数与的图象关于轴对称.
知识点三、指数函数底数变化与图像分布规律
(1)
①,②,③,④,则:
又即:时,(底大幂大)
时,
(2)特殊函数
,,,的图像:
【典型例题】
例1.(2023·重庆市巴川国际高级中学校高一期中)已知函数.
(1)用定义法证明在上单调递增;
(2)若对任意恒成立,求实数的取值范围.
例2.(2023·黑龙江·哈师大附中高一期中)已知函数是奇函数.
(1)求的值,并判断的单调性(不必说明理由);
(2)若存在,使不等式成立,求实数的取值范围.
例3.(2023·江苏·淮阴中学高一期中)已知函数为定义域内的奇函数.
(1)求的值;
(2)设函数,若对任意,总存在使得成立,求实数的取值范围.
例4.(2023·山西省运城中学校高一期中)已知函数是定义域为的奇函数.
(1)求函数的解析式;
(2)判断在上的单调性并用定义证明;
(3)设,求在上的最小值.
例5.(2023·重庆南开中学高一期中)已知函数满足.
(1)求函数的解析式;
(2)若不等式对恒成立,求实数t的取值范围.
【过关测试】
一、单选题
1.(2023·北京二中高一阶段练习)函数的大致图象是( )
A.B.
C.D.
2.(2023·重庆一中高一期中)已知函数的图像恒过定点,则点的坐标是( )
A.B.C.D.
3.(2023·湖南省岳阳县第一中学高一阶段练习)已知函数在上单调递减,则实数的取值范围是( )
A.B.
C.D.
4.(2023·天津·南开大学附属中学高一期中)已知函数,若,则( )
A.B.C.D.
5.(2023·江苏省新海高级中学高一期中)已知函数满足对,都有成立,则实数a的取值范围是( )
A.B.
C.D.
6.(2023·辽宁·育明高中高一期中)若,则( )
A.B.
C.D.
7.(2023·山东青岛·高一期中)设函数,若实数满足:,且,则的取值范围为( )
A.B.C.D.
8.(2023·福建·三明一中高一期中)已知函数,若,则实数的取值范围为( )
A.B.
C.D.
二、多选题
9.(2023·黑龙江·虎林市高级中学高一期中)以下命题正确的是( )
A.,使
B.若函数在上单调递增,则正实数的取值范围是
C.若函数的定义域为,则函数的定义域为
D.函数单调递增区间为
10.(2023·辽宁·渤海大学附属高级中学高一期中)已知函数,,则下列结论正确的是( )
A.为奇函数B.C.D.
11.(2023·江苏·淮阴中学高一期中)已知函数的图象过原点,且无限接近直线,但又不与该直线相交,则下列说法正确的是( )
A.,B.的值域为
C.若,则D.若,且,则
12.(2023·重庆一中高一期中)以下命题中是真命题的有( )
A.若定义在上的函数在是增函数,在也是增函数,则在为增函数
B.若函数是定义在上的单调递增函数,则一定在上单调递增
C.函数,则直线与的图像有1个交点
D.,都有函数在上是单调函数
三、填空题
13.(2023·河南洛阳·高一期中)若函数为奇函数,则实数a=______.
14.(2023·广东东莞·高一期中)已知函数为定义在上的函数满足以下两个条件:
(1)对于任意的实数恒有;(2)在上单调递增.
请写出满足条件的一个的解析式,___________.
15.(2023·安徽·淮北一中高一期中)函数的单调递增区间___________.
16.(2023·重庆市永川北山中学校高一期中)已知函数,若方程恰好有三个实数根,则实数的取值范围是__________.
四、解答题
17.(2023·重庆南开中学高一期中)已知函数的图象过原点,且无限接近直线但又不与该直线相交.
(1)求函数的解析式,并画出的图象;
(2)结合图象,写出不等式的解集.
18.(2023·江苏南通·高一期中)已知奇函数和偶函数的定义域均为,且.
(1)证明:函数在上单调递增;
(2)求函数在区间上的最大值.
19.(2023·北京二中高一阶段练习)设函数.
(1)判断函数的奇偶性并证明;
(2)设,若,求的取值范围.
20.(2023·河南洛阳·高一期中)已知(,且).
(1)解关于x的不等式;
(2)若,且对,,求实数n的取值范围.
21.(2023·广东·深圳市龙岗区龙城高级中学高一期中)已知函数为定义在上的奇函数.
(1)求的值;
(2)根据单调性的定义证明函数在上单调递增;
(3)若对任意实数恒成立,求实数的取值范围.
22.(2023·湖南省岳阳县第一中学高一阶段练习)已知函数是定义在R上的奇函数
(1)求的解析式
(2)若时,恒成立,求实数的取值范围.
时图象
时图象
图象
性质
①定义域,值域
②,即时,,图象都经过点
③,即时,等于底数
④在定义域上是单调减函数
④在定义域上是单调增函数
⑤时,
时,
⑤时,
时,
⑥既不是奇函数,也不是偶函数
专题13 指数函数及其性质
【考点预测】
知识点一、指数函数的概念:
函数(且)叫做指数函数,其中x是自变量,a为常数,函数定义域为.
知识点二、指数函数的图象及性质:
知识点诠释:
(1)当底数大小不定时,必须分“”和“”两种情形讨论.
(2)当时,,;当时,.
当时,的值越大,图象越靠近轴,递增速度越快.
当时,的值越小,图象越靠近轴,递减的速度越快.
(3)指数函数与的图象关于轴对称.
知识点三、指数函数底数变化与图像分布规律
(1)
①,②,③,④,则:
又即:时,(底大幂大)
时,
(2)特殊函数
,,,的图像:
【典型例题】
例1.(2023·重庆市巴川国际高级中学校高一期中)已知函数.
(1)用定义法证明在上单调递增;
(2)若对任意恒成立,求实数的取值范围.
【解析】(1),任取实数,且,;,根据指数函数性质,,又,,,即,根据单调性的定义可得,在上单调递增.
(2),为上的奇函数,
由得:,
由(1)知:在上单调递增,在上恒成立;
当时,,在上恒成立;令,
在上单调递增,在上单调递减,在上单调递增,,,即实数的取值范围为.
例2.(2023·黑龙江·哈师大附中高一期中)已知函数是奇函数.
(1)求的值,并判断的单调性(不必说明理由);
(2)若存在,使不等式成立,求实数的取值范围.
【解析】(1) ,
,
检验:,定义域为,
,
为奇函数,
故.
∴,
∴为增函数.
(2) ,
,
设,
因为,
即存在,使b成立,
当时,,
.
例3.(2023·江苏·淮阴中学高一期中)已知函数为定义域内的奇函数.
(1)求的值;
(2)设函数,若对任意,总存在使得成立,求实数的取值范围.
【解析】(1)因为,是奇函数,所以,解得,
此时,是奇函数.
故.
(2)当时,,故,则,又因为恒成立;
故当时,恒成立,符合条件.
当时,
当时,根据复合函数单调性可得在上单调递增,,
所以,
令,因为都在上单调递增,
故在单调递增,又,所以;
当时,根据复合函数单调性可得在单调递增,在单调递减,
故,所以令,
都是上的单调递增函数,故也是上的单调增函数,
又当时,,故在上恒成立,
故在无解,即不满足条件;
综上所述,.
例4.(2023·山西省运城中学校高一期中)已知函数是定义域为的奇函数.
(1)求函数的解析式;
(2)判断在上的单调性并用定义证明;
(3)设,求在上的最小值.
【解析】(1)∵为奇函数,∴ ,
可得 ,此时,满足,
即函数是定义域为的奇函数,
所以函数的解析式为;
(2)在上为增函数.
证明:设为R上任意两个实数,且,
,
,∴,
∴在上为增函数.
(3)由,
可得,
令 ,
由(2)知为增函数,∵ ,∴ ,
令 ,
当 时, 在 上单调递增,故 ;
当 时,在上单调递减,在 上单调递增,
故 ;
当 时, 在上单调递减,故;
综上所述, .
例5.(2023·重庆南开中学高一期中)已知函数满足.
(1)求函数的解析式;
(2)若不等式对恒成立,求实数t的取值范围.
【解析】(1) ,解得:.
(2),和均为单调递减函数,故为在上单调递减的函数,
又函数的定义域为,则,所以为奇函数,
即对恒成立,
整理得:对恒成立,
当时,不等式等价于对恒成立,,
当时,,
令,,
由于
所以,当时取等,∴,
综上:.
【过关测试】
一、单选题
1.(2023·北京二中高一阶段练习)函数的大致图象是( )
A.B.
C.D.
答案:C
【解析】当时,,因为,所以函数单调递增,
当时,,因为,所以函数单调递减.
故选:C.
2.(2023·重庆一中高一期中)已知函数的图像恒过定点,则点的坐标是( )
A.B.C.D.
答案:A
【解析】对于函数,令,解得,所以,
即函数恒过定点.
故选:A
3.(2023·湖南省岳阳县第一中学高一阶段练习)已知函数在上单调递减,则实数的取值范围是( )
A.B.
C.D.
答案:C
【解析】由题意,
故选:C.
4.(2023·天津·南开大学附属中学高一期中)已知函数,若,则( )
A.B.C.D.
答案:B
【解析】,得,
,即.
故选:B
5.(2023·江苏省新海高级中学高一期中)已知函数满足对,都有成立,则实数a的取值范围是( )
A.B.
C.D.
答案:C
【解析】由题意得在上单调递增,
则,解得,
故选:C
6.(2023·辽宁·育明高中高一期中)若,则( )
A.B.
C.D.
答案:C
【解析】由可得,
令,其中.
则由可得.
又注意到:在R上单调递增,在R上单调递减,
则在R上单调递增.
则由可得,即.
故选:C
7.(2023·山东青岛·高一期中)设函数,若实数满足:,且,则的取值范围为( )
A.B.C.D.
答案:D
【解析】作函数的图象,如图,
设,,
所以,,,
所以,,,
故,
故选:D
8.(2023·福建·三明一中高一期中)已知函数,若,则实数的取值范围为( )
A.B.
C.D.
答案:A
【解析】因为,
,
由,
得
因为单调递减,
所以单调递减,
又时,在上单调递减;
所以,
解得,
所以实数的取值范围为,
故选:A
二、多选题
9.(2023·黑龙江·虎林市高级中学高一期中)以下命题正确的是( )
A.,使
B.若函数在上单调递增,则正实数的取值范围是
C.若函数的定义域为,则函数的定义域为
D.函数单调递增区间为
答案:BD
【解析】解:由题知,关于选项A,不妨令,
单调递减,
,
,即,
,
,故选项A错误;
关于选项B,
在上单调递增,
,解得,故选项B正确;
关于选项C,
的定义域为,
则的定义域为,
解得,故选项C错误;
关于选项D,
为复合函数,
单调递减,
在上单调递减,单调递增,
在上单调递增,单调递减,故选项D正确.
故选:BD
10.(2023·辽宁·渤海大学附属高级中学高一期中)已知函数,,则下列结论正确的是( )
A.为奇函数B.C.D.
答案:ACD
【解析】,,故A正确;
单调递增,∴,故B错误;
,故C正确;
,故D正确.
故选:ACD
11.(2023·江苏·淮阴中学高一期中)已知函数的图象过原点,且无限接近直线,但又不与该直线相交,则下列说法正确的是( )
A.,B.的值域为
C.若,则D.若,且,则
答案:AD
【解析】∵过原点,∴,∴①,
又∵时,,∴时,,
由题知图象无限接近直线,则②,
由①②知,,故A正确;
所以,,,所以B错误;
的图象如下:
由图知,在上单调递减,因为,则,
故C错误;
∵,∴为偶函数,
又∵,且, 在上单调递减,在上单调递增,∴,∴,故D正确.
故选:AD.
12.(2023·重庆一中高一期中)以下命题中是真命题的有( )
A.若定义在上的函数在是增函数,在也是增函数,则在为增函数
B.若函数是定义在上的单调递增函数,则一定在上单调递增
C.函数,则直线与的图像有1个交点
D.,都有函数在上是单调函数
答案:BD
【解析】,显然在是增函数,在也是增函数,而在上不是增函数,所以A项错误;
因为函数是定义在上的单调递增函数,
所以,有,则,
则,
所以一定在上单调递增,B项正确;
显然0不在的定义域内,所以,与的图像没有交点,C项错误;
当时,函数在上单调递增,所以在上是单调函数;
当时,函数对称轴为,当且仅当,即时等号成立,此时可得函数在上是单调递增函数;
当时,函数对称轴为,当且仅当,即时等号成立,此时可得函数在上是单调递增函数.
综上所述,,都有函数在上是单调函数,D项正确.
故选:BD.
三、填空题
13.(2023·河南洛阳·高一期中)若函数为奇函数,则实数a=______.
答案:
【解析】因为是奇函数,所以,
即,所以,
所以.
故答案为:-1.
14.(2023·广东东莞·高一期中)已知函数为定义在上的函数满足以下两个条件:
(1)对于任意的实数恒有;(2)在上单调递增.
请写出满足条件的一个的解析式,___________.
答案:(答案不唯一)
【解析】根据题意,不唯一,不妨取,
因为,且是上的单调增函数,
故满足题意.
故答案为:.
15.(2023·安徽·淮北一中高一期中)函数的单调递增区间___________.
答案:
【解析】令,即,
解得,所以的定义域为,
因为在上递增,在上递减,
且在上递减,
所以的单调增区间为,
故答案为:
16.(2023·重庆市永川北山中学校高一期中)已知函数,若方程恰好有三个实数根,则实数的取值范围是__________.
答案:
【解析】
函数的图象如图所示,
因为恰好有三个实数根,
即函数与的图象有三个交点,
由图象可知,实数的取值范围是.
故答案为:.
四、解答题
17.(2023·重庆南开中学高一期中)已知函数的图象过原点,且无限接近直线但又不与该直线相交.
(1)求函数的解析式,并画出的图象;
(2)结合图象,写出不等式的解集.
【解析】(1)解:由题知,
,
且函数无限接近直线,但又不与该直线相交
∴,即
,
,
为偶函数,只需考虑的图象,
再将的图象关于轴对称,即可得到的图象,
时,,
先将图象横坐标不变,纵坐标扩大为原来的4倍即可得到,
再将图象关于轴对称,即可得到的图象,再将图象向上平移4个单位即可得到,再将的图象去除,将图象关于轴对称,即可得到的图象,所以画图象如下所示:
(2)不妨令,
可得,
结合图象可知不等式的解集为.
18.(2023·江苏南通·高一期中)已知奇函数和偶函数的定义域均为,且.
(1)证明:函数在上单调递增;
(2)求函数在区间上的最大值.
【解析】(1)因为,①
所以.②
因为奇函数和偶函数,
所以.③
②+③得,.
设任意,且,
因为,所以,,
所以,所以函数在上的单调递增.
(2)因为是偶函数,且在上的单调递增,
所以在上的单调递减.
①当即时,
在上的最大值为;
②当即时,
在上的最大值为.
19.(2023·北京二中高一阶段练习)设函数.
(1)判断函数的奇偶性并证明;
(2)设,若,求的取值范围.
【解析】(1)函数是奇函数,证明如下:
函数,,
因为,,且
所以,函数是奇函数.
(2),设,
则,
,,
而,
故,即
在R上是增函数,
若,即
,即,
已知,令
解得或,
①当时,要使,则,
②当时,此时,
要使,则;
③当时,要使,则,
综上,若,当时,的取值范围为;当时,的取值范围为;当时,的取值范围为.
20.(2023·河南洛阳·高一期中)已知(,且).
(1)解关于x的不等式;
(2)若,且对,,求实数n的取值范围.
【解析】(1)可化为,即,
因为恒成立,故.
当,不等式的解集为,
当时,不等式的解集为.
(2)当时,因为,是减函数,
所以是减函数,又因为,
得,即.当时,不等式恒成立,,
当时,不等式两边同除以得:,
因为,当且仅当时等号成立,所以.
综上,实数n的取值范围是.
21.(2023·广东·深圳市龙岗区龙城高级中学高一期中)已知函数为定义在上的奇函数.
(1)求的值;
(2)根据单调性的定义证明函数在上单调递增;
(3)若对任意实数恒成立,求实数的取值范围.
【解析】(1)因为函数为定义在上的奇函数,
所以,得,
经检验符合题意,
所以;
(2)证明:根据(1)知,
,且,
则,
因为,所以,,,
所以,即,
所以函数在上单调递增;
(3)由(2)知,函数为上单调递增的奇函数,
,即,
即,
则,
所以对任意实数恒成立,
当时,,显然成立;
当时,,解得,
综上可知,实数的取值范围是.
22.(2023·湖南省岳阳县第一中学高一阶段练习)已知函数是定义在R上的奇函数
(1)求的解析式
(2)若时,恒成立,求实数的取值范围.
【解析】(1)由题意,是定义在R上的奇函数,则,经检验,满足题意;
故.
(2)由得即
又,故,则;
令,,,
由题意,时,恒成立,
又都在上单调递增,故在上递增,
,故,
即实数的取值范围为.
时图象
时图象
图象
性质
①定义域,值域
②,即时,,图象都经过点
③,即时,等于底数
④在定义域上是单调减函数
④在定义域上是单调增函数
⑤时,
时,
⑤时,
时,
⑥既不是奇函数,也不是偶函数
相关试卷
这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题07函数的概念、定义域、值域、解析式、分段函数(原卷版+解析),共30页。试卷主要包含了函数的概念,区间,函数的三要素,函数的相等,函数的表示方法,分段函数等内容,欢迎下载使用。
这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题06含参数二次函数的最值、单调性、恒成立问题(原卷版+解析),共23页。试卷主要包含了一元二次不等式等内容,欢迎下载使用。
这是一份人教A版高一数学上学期期中期末必考题型归纳及过关测试专题05利用基本不等式求最值(原卷版+解析),共21页。试卷主要包含了重要不等式,基本不等式,与基本不等式相关的不等式,利用基本不等式求最值等内容,欢迎下载使用。









