初中数学鲁教版 (五四制)八年级下册1 一元二次方程教案
展开课题
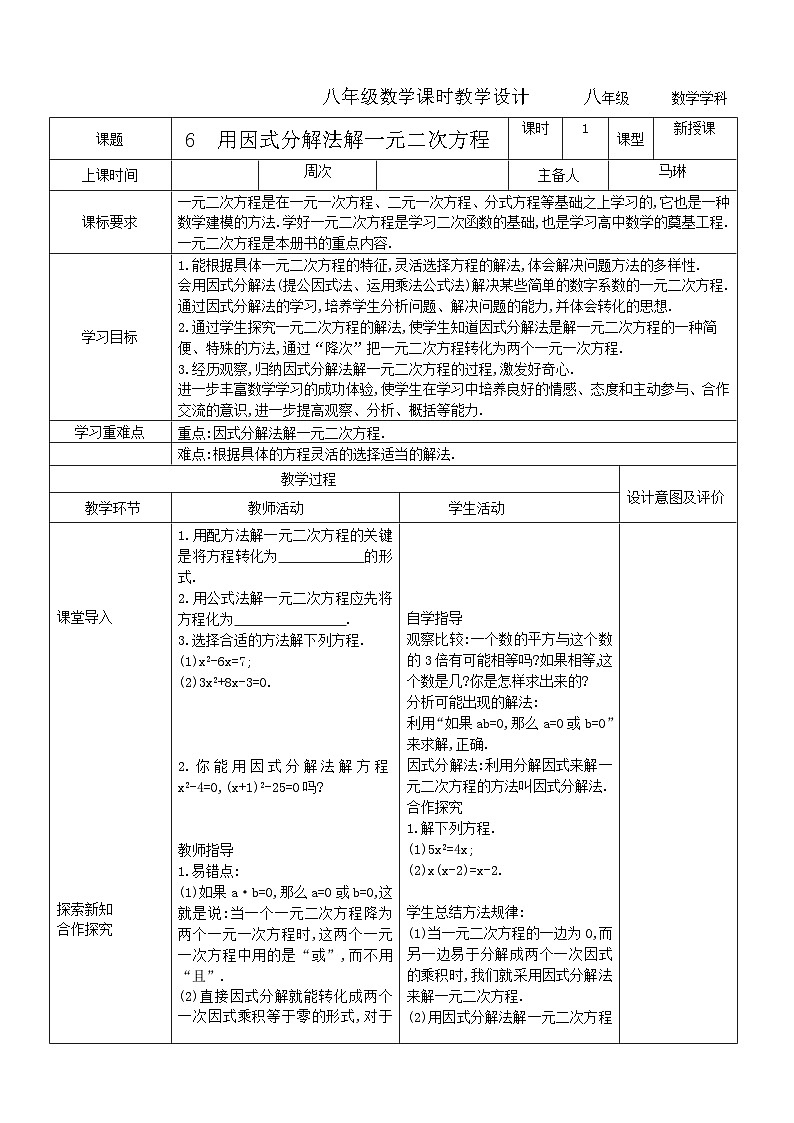
6 用因式分解法解一元二次方程
课时
1
课型
新授课
上课时间
周次
主备人
马琳
课标要求
一元二次方程是在一元一次方程、二元一次方程、分式方程等基础之上学习的,它也是一种数学建模的方法.学好一元二次方程是学习二次函数的基础,也是学习高中数学的奠基工程.一元二次方程是本册书的重点内容.
学习目标
1.能根据具体一元二次方程的特征,灵活选择方程的解法,体会解决问题方法的多样性.
会用因式分解法(提公因式法、运用乘法公式法)解决某些简单的数字系数的一元二次方程.通过因式分解法的学习,培养学生分析问题、解决问题的能力,并体会转化的思想.
2.通过学生探究一元二次方程的解法,使学生知道因式分解法是解一元二次方程的一种简便、特殊的方法,通过“降次”把一元二次方程转化为两个一元一次方程.
3.经历观察,归纳因式分解法解一元二次方程的过程,激发好奇心.
进一步丰富数学学习的成功体验,使学生在学习中培养良好的情感、态度和主动参与、合作交流的意识,进一步提高观察、分析、概括等能力.
学习重难点
重点:因式分解法解一元二次方程.
难点:根据具体的方程灵活的选择适当的解法.
教学过程
设计意图及评价
教学环节
教师活动
学生活动
课堂导入
探索新知
合作探究
当堂训练
1.用配方法解一元二次方程的关键是将方程转化为 的形式.
2.用公式法解一元二次方程应先将方程化为 .
3.选择合适的方法解下列方程.
(1)x2-6x=7; (2)3x2+8x-3=0.
2.你能用因式分解法解方程x2-4=0,(x+1)2-25=0吗?
教师指导
1.易错点:
(1)如果a·b=0,那么a=0或b=0,这就是说:当一个一元二次方程降为两个一元一次方程时,这两个一元一次方程中用的是“或”,而不用“且”.
(2)直接因式分解就能转化成两个一次因式乘积等于零的形式,对于这种形式的方程就不必要整理成一般式了.
2.归纳小结:
(1)当一元二次方程的一边是0,而另一边易于分解成两个一次因式的乘积时,我们就可以用分解因式的方法求解.这种用分解因式解一元二次方程的方法称为因式分解法.
(2)因式分解法的条件是方程左边易于分解,而右边等于零,关键是熟练掌握因式分解的知识,理论依据是“如果两个因式的积等于零,那么至少有一个因式等于零.”
(3)因式分解的方法,突出了转化的思想方法——“降次”,鲜明地显示了“二次”转化为“一次”的过程.
自学指导
观察比较:一个数的平方与这个数的3倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?
分析可能出现的解法:
利用“如果ab=0,那么a=0或b=0”来求解,正确.
因式分解法:利用分解因式来解一元二次方程的方法叫因式分解法.
合作探究
1.解下列方程.
(1)5x2=4x; (2)x(x-2)=x-2.
学生总结方法规律:
(1)当一元二次方程的一边为0,而另一边易于分解成两个一次因式的乘积时,我们就采用因式分解法来解一元二次方程.
(2)用因式分解法解一元二次方程的一般步骤为
①把方程整理使其右边化为0;
②把方程左边分解成两个一次因式的乘积;
③令每个因式分别等于零,得到两个一元一次方程;
④解这两个一元一次方程,它们的解就是原方程的解.
1.方程x2+5x=0的解为( )
(A)x=5 (B)x=-5 (C)x1=0,x2=5 (D)x1=0,x2=-5
2.已知(a+b)(a+b-4)=-4,那么(a+b)= .
3.解方程:
(1)(x+2)(x-4)=0; (2)4x(2x+1)=3(2x+1).
4.一个数平方的2倍等于这个数的7倍,求这个数.
板书设计
教学反思
初中数学鲁教版 (五四制)八年级下册7 利用相似三角形测高教案: 这是一份初中数学鲁教版 (五四制)八年级下册<a href="/sx/tb_c102764_t8/?tag_id=27" target="_blank">7 利用相似三角形测高教案</a>,共2页。
初中数学鲁教版 (五四制)八年级下册6 黄金分割教学设计及反思: 这是一份初中数学鲁教版 (五四制)八年级下册<a href="/sx/tb_c102763_t8/?tag_id=27" target="_blank">6 黄金分割教学设计及反思</a>,共2页。
数学八年级下册4 探索三角形相似的条件教学设计: 这是一份数学八年级下册<a href="/sx/tb_c102761_t8/?tag_id=27" target="_blank">4 探索三角形相似的条件教学设计</a>,共2页。













