

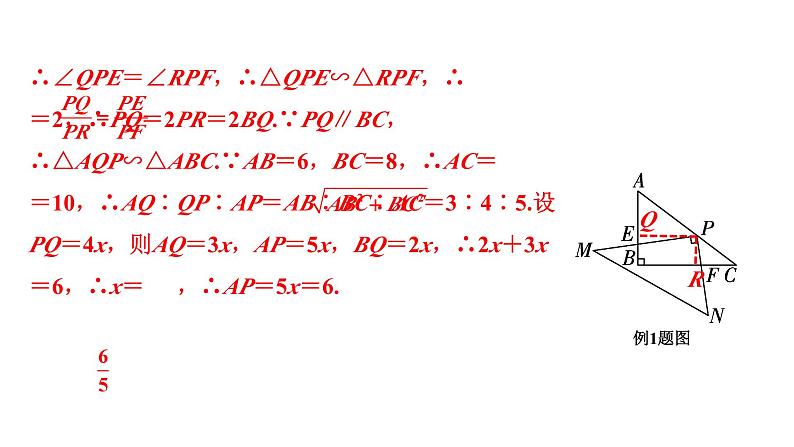

2024成都中考数学第一轮专题复习 微专题 对角互补模型 教学课件
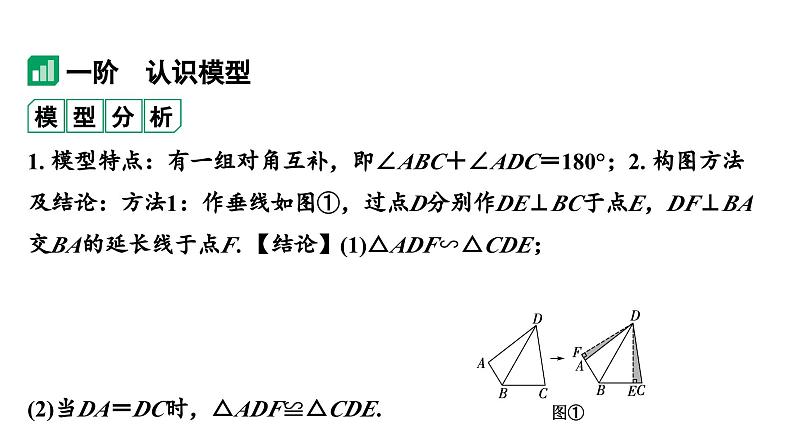
展开1. 模型特点:有一组对角互补,即∠ABC+∠ADC=180°;2. 构图方法及结论:方法1:作垂线如图①,过点D分别作DE⊥BC于点E,DF⊥BA交BA的延长线于点F. 【结论】(1)△ADF∽△CDE;(2)当DA=DC时,△ADF≌△CDE.
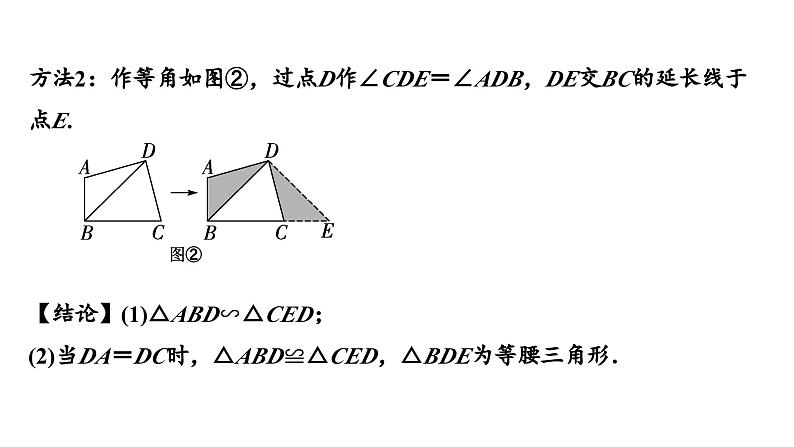
方法2:作等角如图②,过点D作∠CDE=∠ADB,DE交BC的延长线于点E. 【结论】(1)△ABD∽△CED;(2)当DA=DC时,△ABD≌△CED,△BDE为等腰三角形.
例1 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,求AP的长.
解:如图,过点P分别作PQ⊥AB于点Q,PR⊥BC于点R.
∵∠PQB=∠QBR=∠BRP=90°,∴四边形PQBR是矩形,∴∠QPR=90°=∠MPN,∵∠QPE+∠EPR=90°,∠RPF+∠EPR=90°,
∴∠QPE=∠RPF,∴△QPE∽△RPF,∴ =2,∴PQ=2PR=2BQ.∵PQ∥BC,∴△AQP∽△ABC.∵AB=6,BC=8,∴AC= =10,∴AQ∶QP∶AP=AB∶BC∶AC=3∶4∶5.设PQ=4x,则AQ=3x,AP=5x,BQ=2x,∴2x+3x=6,∴x= ,∴AP=5x=6.
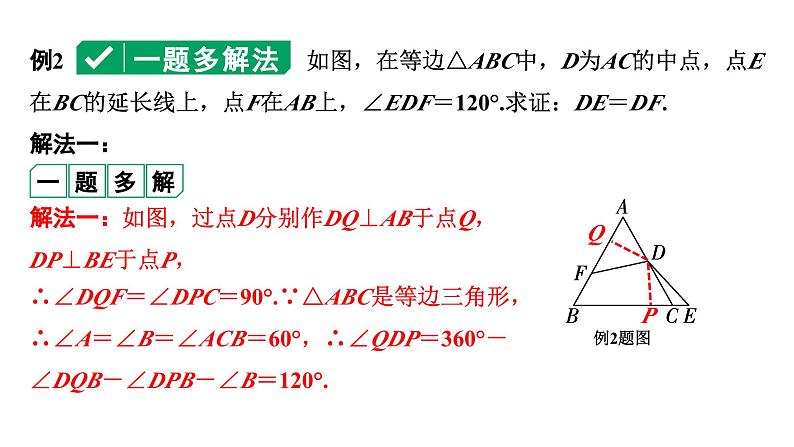
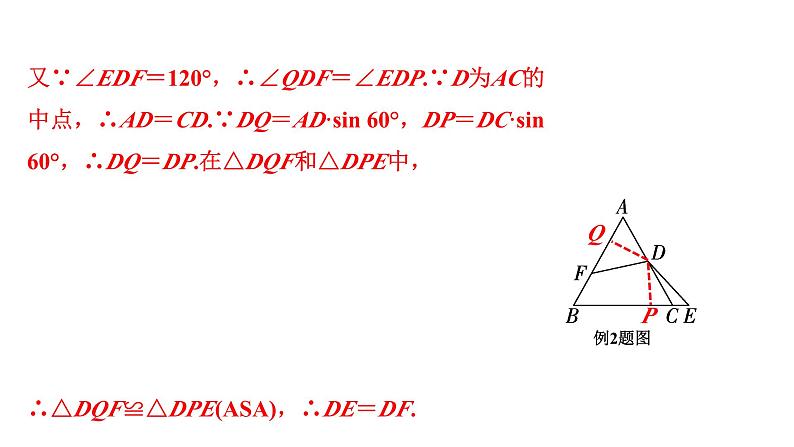
例2 如图,在等边△ABC中,D为AC的中点,点E在BC的延长线上,点F在AB上,∠EDF=120°.求证:DE=DF.
解法一:如图,过点D分别作DQ⊥AB于点Q,DP⊥BE于点P,
∴∠DQF=∠DPC=90°.∵△ABC是等边三角形,∴∠A=∠B=∠ACB=60°,∴∠QDP=360°-∠DQB-∠DPB-∠B=120°.
又∵∠EDF=120°,∴∠QDF=∠EDP.∵D为AC的中点,∴AD=CD.∵DQ=AD·sin 60°,DP=DC·sin 60°,∴DQ=DP.在△DQF和△DPE中, ∴△DQF≌△DPE(ASA),∴DE=DF.
解法二:如解图②,连接BD,以DE为边作∠EDG=∠BDF,点G在BE的延长线上.∵∠EDG=∠BDF,∴∠BDG=∠FDE=120°.∵△ABC是等边三角形,D为AC的中点,∴∠ABD=∠DBC=30°,∴∠DGB=180°-∠BDG-∠DBC=180°-120°-30°=30°,∴∠DGB=∠DBC,∴DB=DG,∴△DBF≌△DGE,∴DE=DF.
1. 如图,△ABC为等边三角形,D为BC边上一点,且CD=3BD,E,F分别为AB,AC上的点,且∠EDF=120°,则 的值为( )A. B. C. D.
2. 如图,在正方形ABCD中,E为AB上一点,F为对角线BD上一点,EF⊥CF,若AD=7,BE=1,则EF的长为________.
3.如图,△ABC是等腰直角三角形,∠ACB=90°,D是斜边AB的中点,E是直线AC上一点,连接DE,DF⊥DE,交直线BC于点F,连接EF.(1)如图①,当点E在线段AC上时,猜想并证明线段EA,EC,EF之间的数量关系;
解:(1)猜想:AE2+EC2=EF2.
证明:如图,连接CD.
∵△ABC是等腰直角三角形,∠ACB=90°,D是斜边AB的中点,∴∠A=∠B=45°,CD⊥AB,AD=CD=DB,
∴∠DCB=∠B=45°,∴∠A=∠DCB,即∠A=∠DCF.∵DF⊥DE,∠ADE+∠EDC=90°,∠CDF+∠EDC=90°,∴∠ADE=∠CDF,在△AED与△CFD中, ∴△AED≌△CFD(ASA),∴AE=CF,在Rt△EFC中,∵CF2+CE2=EF2,∴AE2+EC2=EF2
(2)如图②,当点E在CA的延长线上时,(1)中的猜想是否成立,若成立,请完成证明,若不成立,请写出你的结论并说明理由;
证明:如图,连接CD,
∵在等腰Rt△ABC中,∠ACB=90°,∴∠CAB=∠B=45°.∵CD为AB的中线,∴CD⊥AB,AD=CD=BD,∠ACD=∠BCD=45°,∴∠EAD=180°-∠CAD=135°,∠FCD=180°-∠BCD=135°,
∴∠EAD=∠FCD.∵DF⊥DE,∴∠ADE+∠ADF=∠CDF+∠ADF=90°,∴∠ADE=∠CDF,在△AED与△CFD中, ∴△AED≌△CFD(ASA),∴AE=CF,在Rt△EFC中,∵CF2+CE2=EF2,∴AE2+EC2=EF2;
(3)点E在直线AC上移动,当EA= EC时,求∠ADE的度数.
(3)由(1)可知AE2+EC2=EF2,∵AE= EC,∴( EC)2+EC2=EF2,∴EF=2EC.∵∠ECF=90°,∴∠FEC=60°.∵△AED≌△CFD,∴ED=FD.∵∠EDF=90°,∴∠FED=45°,①当E在线段AC上时,如解图③∴∠AEF=180°-∠FEC=180°-60°=120°,
∴∠AED=∠AEF-∠FED=120°-45°=75°.∵∠CAB=45°,∴∠ADE=180°-45°-75°=60°;②当E在AC延长线上时,如解图④,∵∠FEC=60°,∠FED=45°,∴∠AED=∠FEC-∠FED=60°-45°=15°.∵∠CAB=45°,∴∠ADE=180°-15°-45°=120°.综上可知∠ADE的度数为60°或120°.
E在直线AC上,需分点E在线段AC上和点E在线段AC的延长线上两种情况讨论.
中考数学二轮专题复习 课件: 对角互补模型: 这是一份中考数学二轮专题复习 课件: 对角互补模型,共19页。PPT课件主要包含了△ADF∽△CDE,AD=CD,二轮专题复习,△ABD∽△CED,∠BCA=∠DCA,∠BAF,正方形,∠ADF,二阶综合训练等内容,欢迎下载使用。
中考数学复习第四章三角形重难突破微专题(六)对角互补模型教学课件: 这是一份中考数学复习第四章三角形重难突破微专题(六)对角互补模型教学课件,共16页。PPT课件主要包含了AE=AF等内容,欢迎下载使用。
中考数学复习第四章三角形重难突破微专题(六)对角互补模型教学课件: 这是一份中考数学复习第四章三角形重难突破微专题(六)对角互补模型教学课件,共16页。PPT课件主要包含了AE=AF等内容,欢迎下载使用。












