九年级数学下册专题05相似三角形中的基本模型之对角互补模型(原卷版+解析)

这是一份九年级数学下册专题05相似三角形中的基本模型之对角互补模型(原卷版+解析)，共45页。试卷主要包含了对角互补模型，5°，从而得到∠DAC=22，5x等内容，欢迎下载使用。
模型1.对角互补模型（相似模型）
【模型解读】四边形或多边形构成的几何图形中，相对的角互补。该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形相似.
【常见模型及结论】
1）对角互补相似1
条件：如图，在Rt△ABC中，∠C＝∠EOF＝90°，点O是AB的中点，

辅助线：过点O作OD⊥AC，垂足为D，过点O作OH⊥BC，垂足为H，
结论：①△ODE∼△OHF；②（思路提示：）.
2）对角互补相似2
条件：如图，已知∠AOB＝∠DCE＝90°，∠BOC＝.

辅助线：作法1：如图1，过点C作CF⊥OA，垂足为F，过点C作CG⊥OB，垂足为G；
结论：①△ECG∼△DCF；②CE＝CD·.（思路提示：，CF=OG，在Rt△COG中，）
辅助线：作法2：如图2，过点C作CF⊥OC，交OB于F；
结论：①△CFE∼△COD；②CE＝CD·.（思路提示：，在Rt△OCF中，）
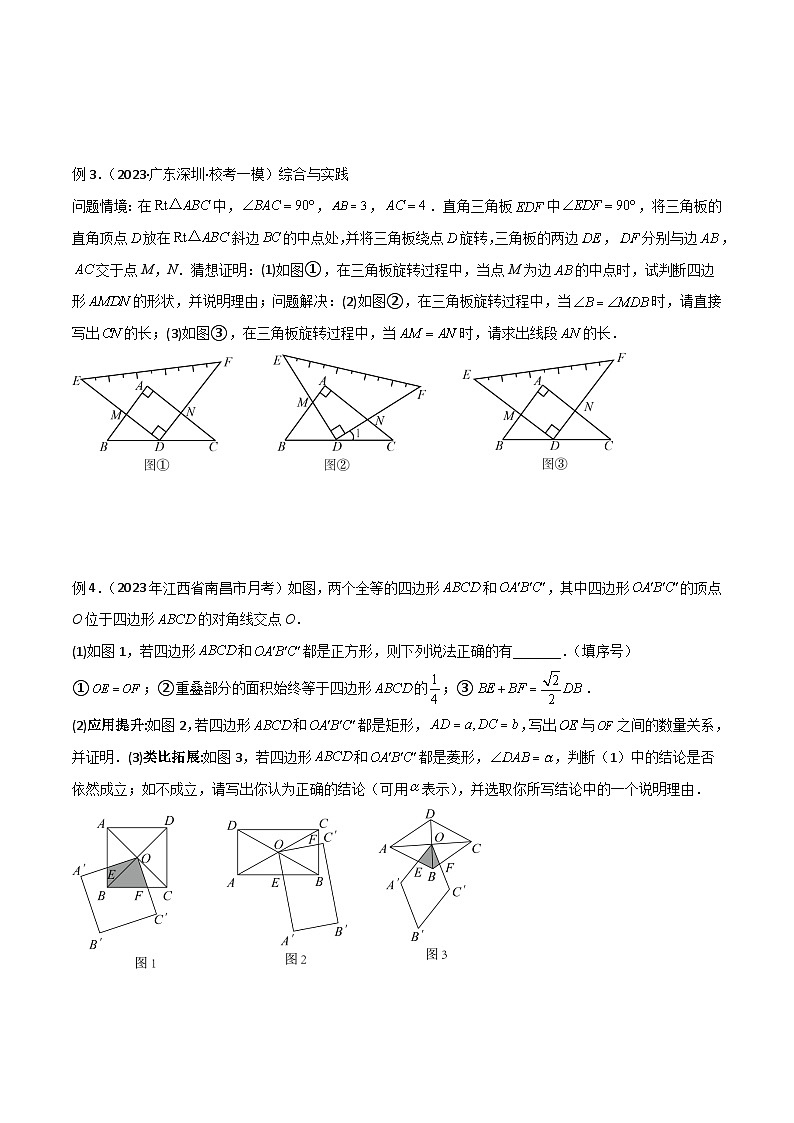
3）对角互补相似3
条件：已知如图，四边形ABCD中，∠B+∠D=180°
辅助线：过点D作DE⊥BA，垂足为E，过点D作DF⊥BC，垂足为F；
结论：①△DAE∼△DCF；②ABCD四点共圆。
例1．（2023·重庆·九年级期中）如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，在Rt△MPN中，∠MPN＝90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE＝2PF时，AP＝________．
例2．（2023·河南南阳·九年级统考阶段练习）如图，在等腰直角中，，，过点作射线，为射线上一点，在边上（不与重合）且，与交于点．（1）求证：；（2）求证：；（3）如果，求证：．
例3．（2023·广东深圳·校考一模）综合与实践
问题情境：在中，，，．直角三角板中，将三角板的直角顶点放在斜边的中点处，并将三角板绕点旋转，三角板的两边，分别与边，交于点M，N．猜想证明：(1)如图①，在三角板旋转过程中，当点M为边的中点时，试判断四边形的形状，并说明理由；问题解决：(2)如图②，在三角板旋转过程中，当时，请直接写出的长；(3)如图③，在三角板旋转过程中，当时，请求出线段的长．

例4．（2023年江西省南昌市月考）如图，两个全等的四边形和，其中四边形的顶点O位于四边形的对角线交点O．
(1)如图1，若四边形和都是正方形，则下列说法正确的有_______．（填序号）
①；②重叠部分的面积始终等于四边形的；③．
(2)应用提升:如图2，若四边形和都是矩形，，写出与之间的数量关系，并证明．(3)类比拓展:如图3，若四边形和都是菱形，，判断（1）中的结论是否依然成立；如不成立，请写出你认为正确的结论（可用表示），并选取你所写结论中的一个说明理由．
例5．（2023.辽宁中考模拟）如图，在RtABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O逆时针旋转90°，交射线CB于点N．（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；
（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；
（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且＜，请直接写出的值（用含k的式子表示）．
例6．（2023浙江中考二模）（1）特例感知：如图1，已知在RtABC中，∠BAC＝90°，AB＝AC，取BC边上中点D，连接AD，点E为AB边上一点，连接DE，作DF⊥DE交AC于点F，求证：BE＝AF；
（2）探索发现：如图2，已知在RtABC中，∠BAC＝90°，AB＝AC＝3，取BC边上中点D，连接AD，点E为BA延长线上一点，AE＝1，连接DE，作DF⊥DE交AC延长线于点F，求AF的长；
（3）类比迁移：如图3，已知在ABC中，∠BAC＝120°，AB＝AC＝4，取BC边上中点D，连接AD，点E为射线BA上一点（不与点A、点B重合），连接DE，将射线DE绕点D顺时针旋转30°交射线CA于点F，当AE＝4AF时，求AF的长．
课后专项训练
1．（2023广东九年级期中）如图，中，，平分，，连接，并延长分别交，于点和点，若，，则的长为（ ）
A．10B．12C．15D．16
2．（2023·山西临汾·统考二模）在菱形中，，对角线交于点，分别是边上的点，且与交于点，则的值为 ．

3．（2023·江苏扬州·八年级校考阶段练习）如图，已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则= .
4．（2023·江苏扬州·八年级校考阶段练习）如图，已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则= .
5．（2023青岛版九年级月考）如图，在中，，，直角的顶点在上，、分别交、于点、，绕点任意旋转．当时，的值为 ；当时，为 ．（用含的式子表示）
6．（2023春·浙江嘉兴·九年级校考阶段练习）已知一块含的直角三角板ABC按图1放置，其中，点B与原点O重合，，．现将点A沿y轴向下滑动，同时点B沿x轴向右滑动，当点A滑动至与原点O重合时停止． 当四边形为矩形时（如图2），点C的坐标为 ；当点A滑动到原点O时，点C经过的路径长为 ．

7．（2023年河南一模数学试题）如图，在菱形中，，，对角线，交于点，，分别是，边上的点，且，，与交于点，则的值为 ．

8．（2023.广东九年级期中）如图，在中，，， ，，，点在上，交于点，交于点，当时， ．
9．（2023年福建泉州中考数学模拟试卷）如图，在Rt△ABC中，∠A=90°，AB=12，AC=16，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°．
（1）求ED、EC的长；（2）若BP=2，求CQ的长；（3）若线段PQ与线段DE的交点为F，当△PDF为等腰三角形时，求BP的长．
10．（2022春·四川达州·九年级专题练习）已知，在中，．
（1）如图1，已知点D在边上，，连结．试探究与的关系；
（2）如图2，已知点D在下方，，连结．若，，，交于点F，求的长；（3）如图3，已知点D在下方，连结、、．若，，，，求的值．
11．（2023辽宁铁岭市中考模拟）如图，中，，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且．
（1）如图1，当时，线段AG和CF的数量关系是 ．
（2）如图2，当时，猜想线段AG和CF的数量关系，并加以证明．
（3）若，，，请直接写出CF的长．
12．（2023西南交通大学附属中学九年级月考）在中，，，，点为边的中点，交边于点，点为直线上的一动点，点为直线上的一动点，且．
（1）求、的长．（2）若，求的长．（3）记线段与线段的交点为点，若为等腰三角形，求的长．
13．（2022秋·山西吕梁·九年级校考阶段练习）综合与实践
问题情境：在中，．点在斜边上运动，过点作射线，分别与边交于点．猜想证明：（1）当点在斜边的中点处时，

①如图（1），在旋转过程中，当点时，与的数量关系是______，_______．
②当旋转到如图②所示的位置时，的值是否发生变化？若不变，请证明；若变化，请说明理由．
③如图③，在旋转过程中，当时，直接写出线段的长_______；
类比探究（2）当点在斜边上运动时，
①如图④，当点运动到时，_______；
②如图⑤，连接，当是等腰三角形时，求的长．
14．（2023秋·山西忻州·九年级校考期末）综合与实践
问题情境：在学习了三角形的相似后，同学们开始了对不同三角形中的相似模型的探究．
猜想推理：

（1）如图1，在等边中，D为边上一点，E为边上一点，，，，则______．问题解决：（2）如图2，是等边三角形，D是的中点，射线，分别交，于点E，F，且，求证：．（3）如图3，，，，D是的中点，射线，分别交，于点E，F，且，求的值．
15．（2023广东深圳三模试题）（1）【探究发现】如图1，正方形的对角线相交于点，在正方形绕点旋转的过程中，边与边交于点，边与边交于点．证明：；

（2）【类比迁移】如图2，矩形的对角线相交于点，且，．在矩形绕点旋转的过程中，边与边交于点，边与边交于点．若，求的长；
（3）【拓展应用】如图3，四边形和四边形都是平行四边形，且，，，是直角三角形．在绕点旋转的过程中，边与边交于点，边与边交于点．当与重叠部分的面积是的面积的时，请直接写出的长．

专题05 相似三角形中的基本模型之对角互补模型
相似三角形在中考数学几何模块中占据着重要地位。相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了。本专题就对角互补模型进行梳理及对应试题分析，方便掌握。
模型1.对角互补模型（相似模型）
【模型解读】四边形或多边形构成的几何图形中，相对的角互补。该题型常用到的辅助线主要是顶定点向两边做垂线，从而证明两个三角形相似.
【常见模型及结论】
1）对角互补相似1
条件：如图，在Rt△ABC中，∠C＝∠EOF＝90°，点O是AB的中点，

辅助线：过点O作OD⊥AC，垂足为D，过点O作OH⊥BC，垂足为H，
结论：①△ODE∼△OHF；②（思路提示：）.
2）对角互补相似2
条件：如图，已知∠AOB＝∠DCE＝90°，∠BOC＝.

辅助线：作法1：如图1，过点C作CF⊥OA，垂足为F，过点C作CG⊥OB，垂足为G；
结论：①△ECG∼△DCF；②CE＝CD·.（思路提示：，CF=OG，在Rt△COG中，）
辅助线：作法2：如图2，过点C作CF⊥OC，交OB于F；
结论：①△CFE∼△COD；②CE＝CD·.（思路提示：，在Rt△OCF中，）
3）对角互补相似3
条件：已知如图，四边形ABCD中，∠B+∠D=180°
辅助线：过点D作DE⊥BA，垂足为E，过点D作DF⊥BC，垂足为F；
结论：①△DAE∼△DCF；②ABCD四点共圆。
例1．（2023·重庆·九年级期中）如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，在Rt△MPN中，∠MPN＝90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE＝2PF时，AP＝________．
【答案】3
【分析】如图作PQ⊥AB于Q，PR⊥BC于R．由△QPE∽△RPF，可得PQ=2PR=2BQ，由PQ∥BC，可得AQ：QP：AP=AB：BC：AC=3：4：5，设PQ=4x，则AQ=3x，AP=5x，BQ=2x，可得2x+3x=3，求出x即可解决问题．
【详解】解：如图作PQ⊥AB于点Q，PR⊥BC于点R．
∵∠PQB＝∠QBR＝∠BRP＝90°，∴四边形PQBR是矩形，
∴∠QPR＝90°＝∠MPN，∴∠QPE＝∠RPF，∴，
，，∵PQ//BC，
设PQ＝4x，则AQ＝3x，AP＝5x，BQ＝2x，∴2x＋3x＝3∴，∴AP＝5x＝3．故答案为3．
【点睛】本题考查相似三角形的判定和性质、勾股定理、矩形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考常考题型．
例2．（2023·河南南阳·九年级统考阶段练习）如图，在等腰直角中，，，过点作射线，为射线上一点，在边上（不与重合）且，与交于点．（1）求证：；（2）求证：；（3）如果，求证：．
【答案】（1）见解析；（2）见解析；（3）见解析
【分析】（1）根据题意先由等腰直角△ABC得到∠BAC=∠B=45°，从而结合∠DAE=45°得到∠DAC=∠EAB，再由平行线的性质得到∠ACP=∠BAC=∠B=45°，从而得到△ADC∽△AEB；
（2）根据题意由相似三角形的性质得到AD：AE=AC：AB，转化为AD：AC=AE：AB，结合∠DAE=∠CAB=45°得证结果；（3）根据题意结合∠ACD=45°和∠ACB=90°，由CD=CE得到∠CDE=∠CED=22.5°，从而得到∠DAC=22.5°，然后得到△OCD∽△DCA，最后即可求证．
【详解】解：（1）证明：∵是等腰直角三角形，∴，
∵，，∴，，∴；
（2）证明：∵∴，即，
∵，∴；
（3）∵，∴，
∵，∴，∵，∴，
∴∴，
又∵，∴，∴，∴
【点睛】本题考查相似三角形的判定与性质以及等腰直角三角形的性质，解题的关键是通过线段的比例关系得到三角形相似．
例3．（2023·广东深圳·校考一模）综合与实践
问题情境：在中，，，．直角三角板中，将三角板的直角顶点放在斜边的中点处，并将三角板绕点旋转，三角板的两边，分别与边，交于点M，N．

猜想证明：(1)如图①，在三角板旋转过程中，当点M为边的中点时，试判断四边形的形状，并说明理由；
问题解决：(2)如图②，在三角板旋转过程中，当时，请直接写出的长；
(3)如图③，在三角板旋转过程中，当时，请求出线段的长．
【答案】(1)四边形是矩形，理由见解析(2)(3)
【分析】（1）由三角形中位线定理可得，可证，即可求解；
（2）由勾股定理可求的长，由中点的性质可得的长，由锐角三角函数可求解；（3）通过证明点，点，点，点四点共圆，可得，由直角三角形的性质可求的长，即可求解．
【详解】（1）解：四边形是矩形，理由如下：
点是的中点，点是的中点，，，
，，
，四边形是矩形；
（2）如图2，过点作于，

，，，，点是的中点，，
，，，，，
又，，，，；
（3）如图③，连接，，过点作于，

，，，
，点，点，点，点四点共圆，，
，，，
，，，，
，，
，，，
．
【点睛】本题是三角形综合题，考查了矩形的判定，直角三角形的性质，勾股定理，锐角三角函数，圆的有关知识，灵活运用这些性质解决问题是解题的关键．
例4．（2023年江西省南昌市月考）如图，两个全等的四边形和，其中四边形的顶点O位于四边形的对角线交点O．
(1)如图1，若四边形和都是正方形，则下列说法正确的有_______．（填序号）
①；②重叠部分的面积始终等于四边形的；③．
(2)应用提升:如图2，若四边形和都是矩形，，写出与之间的数量关系，并证明．
(3)类比拓展:如图3，若四边形和都是菱形，，判断（1）中的结论是否依然成立；如不成立，请写出你认为正确的结论（可用表示），并选取你所写结论中的一个说明理由．
【答案】(1)①②③(2)关系为，证明见解析
(3)①成立，②③不成立，正确结论②重叠部分的面积始终等于四边形的；③．证明①的过程见解析
【详解】（1）如图，在图1中，过点O作于点H,于点G
∵于点H, 于点G∴
∵四边形和都是正方形∴∴
∵,∴
在和中∴∴故①正确
∵∴∴故②正确
∵四边形是正方形∴
∴故③正确
（2）关系为，证明如下：如图，在图2中，过点O作于点H,于点G
∵于点H, 于点G∴
∵四边形和都是矩形∴
∵,∴
在和中∴∴
（3）（1）中结论，①成立，②③不成立，正确结论②重叠部分的面积始终等于四边形的；③．现证明①如下：
如图，在图3中，过点O作于点H,于点G
∵于点H, 于点G∴
∵四边形和都是菱形∴∴
∵,∴
在和中∴∴
例5．（2023.辽宁中考模拟）如图，在RtABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O逆时针旋转90°，交射线CB于点N．（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；
（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；
（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且＜，请直接写出的值（用含k的式子表示）．
【答案】（1）OM＝ON，见解析；（2）ON＝k•OM，见解析；（3）
【分析】（1）作OD⊥AM，OE⊥BC，证明△DOM≌△EON；（2）作OD⊥AM，OE⊥BC，证明△DOM∽△EON；（3）设AC＝BC＝a，解Rt△EON和斜△AOM，用含的代数式分别表示再利用比例的性质可得答案．
【详解】解：（1）OM＝ON，如图1，作OD⊥AM于D，OE⊥CB于E，

∴∠ADO＝∠MDO＝∠CEO＝∠OEN＝90°，∴∠DOE＝90°，
∵AC＝BC，∠ACB＝90°，∴∠A＝∠ABC＝45°，
在Rt△AOD中，，同理：OE＝OB，
∵OA＝OB，∴OD＝OE，∵∠DOE＝90°，∴∠DOM＋∠MOE＝90°，
∵∠MON＝90°，∴∠EON＋∠MOE＝90°，∴∠DOM＝∠EON，
在Rt△DOM和Rt△EON中，，∴△DOM≌△EON（ASA），∴OM＝ON．
（2）如图2，作OD⊥AM于D，OE⊥BC于E，由（1）知：OD＝OA，OE＝OB，
∴，由（1）知：∠DOM＝∠EON，∠MDO＝∠NEO＝90°，
∴△DOM∽△EON，∴，∴ON＝k•OM．
（3）如图3，设AC＝BC＝a，∴AB＝a，
∵OB＝k•OA，∴OB＝•a，OA＝•a，∴OE＝OB＝a，
∵∠N＝∠ABC﹣∠BON＝45°﹣15°＝30°，∴EN＝＝OE＝•a，
∵CE＝OD＝OA＝a，∴NC＝CE＋EN＝a＋•a，
由（2）知：，△DOM∽△EON，∴∠AMO＝∠N＝30°
∵，∴，∴△PON∽△AOM，∴∠P＝∠A＝45°，
∴PE＝OE＝a，∴PN＝PE＋EN＝a＋•a，
设AD＝OD＝x，∴DM＝，由AD＋DM＝AC＋CM得，（＋1）x＝AC＋CM，
∴x＝（AC＋CM）＜（AC＋AC）＝AC，∴k＞1
∴，
∴．
【点睛】本题考查了三角形全等和相似，以及解直角三角形，解决问题的关键是作OD⊥AC，OE⊥BC；本题的难点是条件得出k＞1．
例6．（2023浙江中考二模）（1）特例感知：如图1，已知在RtABC中，∠BAC＝90°，AB＝AC，取BC边上中点D，连接AD，点E为AB边上一点，连接DE，作DF⊥DE交AC于点F，求证：BE＝AF；
（2）探索发现：如图2，已知在RtABC中，∠BAC＝90°，AB＝AC＝3，取BC边上中点D，连接AD，点E为BA延长线上一点，AE＝1，连接DE，作DF⊥DE交AC延长线于点F，求AF的长；
（3）类比迁移：如图3，已知在ABC中，∠BAC＝120°，AB＝AC＝4，取BC边上中点D，连接AD，点E为射线BA上一点（不与点A、点B重合），连接DE，将射线DE绕点D顺时针旋转30°交射线CA于点F，当AE＝4AF时，求AF的长．
【答案】（1）见解析；（2）4；（3）或或
【分析】（1）证明△BDE≌△ADF（ASA），根据全等三角形的性质即可得到BE＝AF；
（2）方法同（1），利用全等三角形的性质解决问题；
（3）证明△EBD∽△DCF，推出，设AF＝m，则AE＝4m，分三种情形，分别构建方程求解即可．
【详解】（1）证明：如图1中，
∵△ABC中，∠BAC＝90°，AB＝AC，AD是高，
∴BD＝CD＝ADBC，∠B＝∠C＝45°，∠BAD＝∠CAD∠BAC＝45°，
∵DF⊥DE，∴∠EDF＝∠ADB＝90°，∴∠BDE＝∠ADF＝90°﹣∠ADE，
在△BDE和△ADF中，，∴△BDE≌△ADF（ASA），∴BE＝AF；
（2）解：如图2中，
由（1）知，BD＝CD＝AD，∠B＝∠C＝∠BAD＝∠CAD＝45°，
∴∠EDF＝∠ADB＝90°，∴∠BDE＝∠ADF＝90°+∠ADE，
在△BDE和△ADF中，，∴△BDE≌△ADF（ASA），∴BE＝AF，
∵AB＝3，AE＝1，∴BE＝AB+AE＝4，∴AF＝4；
（3）解：如图3中，
∵AB＝AC，BD＝CD，∴AD⊥BC，∠BAD＝∠CAD∠BAC＝60°，∴BD＝CD＝AB•sin60°＝2，
∵AE＝4AF，∴可以假设AF＝m，则AE＝4m，BE＝4﹣4m，CF＝4﹣m，
∵∠EDC＝∠EDF+∠FDC＝∠B+∠BED，∠EDF＝∠B＝30°，
∴∠FDC＝∠BED，∵∠B＝∠C，∴△EBD∽△DCF，∴，
∴，整理得，m2﹣5m+1＝0，解得m或（舍弃），
经检验，m是分式方程的解．
当点F在CA的延长线上时，CF＝4+m，由△EBD∽△DCF，可得，
∴，解得，m或（舍弃），经检验，m是分式方程的解．
当点E在射线BA上时，BE＝4+4m，
∵△EBD∽△DCF，∴，∴
解得，m或（舍弃），
经检验，m是分式方程的解．
综上所述，满足条件的AF的值为或或．
【点睛】本题属于几何变换综合题，考查了全等三角形的判定与性质、相似三角形的判定与性质，等腰直角三角形的判定与性质等知识；熟练掌握等腰直角三角形的判定与性质，证明三角形全等是解题的关键，学会用分类讨论的思想思考问题，属于中考常考题型．
课后专项训练
1．（2023广东九年级期中）如图，中，，平分，，连接，并延长分别交，于点和点，若，，则的长为（ ）
A．10B．12C．15D．16
【答案】C
【分析】由四点共圆，得到，再证明，得到与的比，延长到，使，得到为等边三角形，在证明出，证出与，利用即可求出．
【详解】解：，，、、、四点共圆，
平分，，，
，，
，，，
如图，延长到，使，
，为等边三角形，，
，，设每一份为，
，，，，
．故选：C．
【点睛】本题考查了三角形相似的性质、等边三角形的性质等知识点的应用，四点共圆的应用及相似比的转化是解题关键．
2．（2023·山西临汾·统考二模）在菱形中，，对角线交于点，分别是边上的点，且与交于点，则的值为 ．

【答案】
【分析】由菱形的性质及可证，得，；由得，，于是，可得，进而求得答案．
【详解】∵
∴∴
∵四边形是菱形，∴，
∴∴∴，
又∵∴．，
∵∴，
∴．
设，则，，
；故答案为：．
【点睛】本题考查菱形的性质，全等三角形的判定和性质，相似三角形的判定和性质，利用全等及相似得到线段间的数量关系是解题的关键．
3．（2023·江苏扬州·八年级校考阶段练习）如图，已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则= .
【答案】
【分析】过D作DG∥BC交AB于G，则DG为△ABC的中位线，根据等边三角形的性质得∠ACB＝∠ABC＝60°，由DG∥BC，得∠FGD＝120°，∠GDC＝120°，△AGD为等边三角形，而∠EDF＝120°，得∠GDF＝∠CDE，易证得△GDF∽△CDE，所以FG：CE＝DG：DC，即CE：DC＝FG：DG＝FG：AG，设BF＝x，AF＝2x，则AB＝3x，AG＝1.5x，FG＝1.5x−x＝0.5x，即可得到CE：CD的比值．
【详解】解：过D作DG∥BC交AB于G，如图，
∵D是AC的中点，∴DG为△ABC的中位线，
∵△ABC是等边三角形，∴∠ACB＝∠ABC＝60°，∴∠DCE＝120°，
又∵DG∥BC，∴∠FGD＝120°，∠GDC＝120°，△AGD为等边三角形，
∵∠EDF＝120°，∴∠GDF＝∠CDE，∴△GDF∽△CDE，
∴FG：CE＝DG：CD，即CE：CD＝FG：DG，而DG＝AG＝BG，AF＝2BF，
设BF＝x，AF＝2x，则AB＝3x，AG＝1.5x，FG＝1.5x−x＝0.5x，
∴CE：CD＝FG：DG＝FG：AG＝0.5x：1.5x＝1：3．故答案为．
【点睛】本题考查了等边三角形的性质：等边三角形三边相等；三个角都等于60°；也考查了相似三角形的判定与性质，熟练应用各性质进行推理计算是解题关键．
4．（2023·江苏扬州·八年级校考阶段练习）如图，已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则= .
【答案】
【分析】过D作DG∥BC交AB于G，则DG为△ABC的中位线，根据等边三角形的性质得∠ACB＝∠ABC＝60°，由DG∥BC，得∠FGD＝120°，∠GDC＝120°，△AGD为等边三角形，而∠EDF＝120°，得∠GDF＝∠CDE，易证得△GDF∽△CDE，所以FG：CE＝DG：DC，即CE：DC＝FG：DG＝FG：AG，设BF＝x，AF＝2x，则AB＝3x，AG＝1.5x，FG＝1.5x−x＝0.5x，即可得到CE：CD的比值．
【详解】解：过D作DG∥BC交AB于G，如图，
∵D是AC的中点，∴DG为△ABC的中位线，
∵△ABC是等边三角形，∴∠ACB＝∠ABC＝60°，∴∠DCE＝120°，
又∵DG∥BC，∴∠FGD＝120°，∠GDC＝120°，△AGD为等边三角形，
∵∠EDF＝120°，∴∠GDF＝∠CDE，∴△GDF∽△CDE，
∴FG：CE＝DG：CD，即CE：CD＝FG：DG，而DG＝AG＝BG，AF＝2BF，
设BF＝x，AF＝2x，则AB＝3x，AG＝1.5x，FG＝1.5x−x＝0.5x，
∴CE：CD＝FG：DG＝FG：AG＝0.5x：1.5x＝1：3．故答案为．
【点睛】本题考查了等边三角形的性质：等边三角形三边相等；三个角都等于60°；也考查了相似三角形的判定与性质，熟练应用各性质进行推理计算是解题关键．
5．（2023青岛版九年级月考）如图，在中，，，直角的顶点在上，、分别交、于点、，绕点任意旋转．当时，的值为 ；当时，为 ．（用含的式子表示）
【答案】 ,
【详解】如图，过点O作OH⊥AC于H，OG⊥BC于G，由条件可以表示出HO、GO的值，通过证明△PHO∽△QGO由相似三角形的性质就可以求出结论．
解答：解：过点O作OH⊥AC于H，OG⊥BC于G，∴∠OHP=∠OGQ=90°．
∵∠ACB=90°，∴四边形HCGO为矩形，
∴∠HOG=90°，∴∠HOP=∠GOQ，∴△PHO∽△QGO，∴．
∵，设OA=x，则OB=2x，且∠ABC=30°，∴AH=x，OG=x．
在Rt△AHO中，由勾股定理，得OH=x，∴，∴=．故答案为．
6．（2023春·浙江嘉兴·九年级校考阶段练习）已知一块含的直角三角板ABC按图1放置，其中，点B与原点O重合，，．现将点A沿y轴向下滑动，同时点B沿x轴向右滑动，当点A滑动至与原点O重合时停止． 当四边形为矩形时（如图2），点C的坐标为 ；当点A滑动到原点O时，点C经过的路径长为 ．

【答案】 2
【分析】在中，求得，的长度，再根据矩形的性质，即可求解；确定出点的运动轨迹，即可求解．
【详解】解：由题意可得： 在中，，
∴，
∴当四边形为矩形，，∴点的坐标为；
作，轴，连接，如下图：

∵，，
∴四边形为矩形，，
∵∴∴
∴，即
因此点在直线上运动，且当四边形为矩形时，点运动到最高点，点移动到时，运动到最低点，可作图如下，点运动路径为，三点共线，

∵四边形为矩形，∴，
∵，∴．故答案为：，．
【点睛】此题考查了坐标与图形，矩形的性质，相似三角形的判定与性质，含直角三角形的性质，解题的关键是熟练掌握相关基础性质，通过作辅助线确定出点的运动轨迹．
7．（2023年河南省周口市一模数学试题）如图，在菱形中，，，对角线，交于点，，分别是，边上的点，且，，与交于点，则的值为 ．

【答案】或1
【分析】先证，接着在中利用勾股定理求出所需线段的长度，最后利用正切的定义求解．
【详解】解：在菱形中，，∴为等边三角形，
∴，.
∵，，
∴，∴.
如图，过点作于点.在中，，
∴，∴.
设，则，.

在中，，即，解得，.
当时，，，
∴，即，解得，
∴，∴.
当时，，
，即，解得，
∴，∴ 综上可知，的值为或1.
【点睛】本题考查了全等三角形的判定与性质、勾股定理的应用、正切的定义等．综合性较强，需要学生具有较强的几何推理能力．
8．（2023.广东九年级期中）如图，在中，，， ，，，点在上，交于点，交于点，当时， ．
【答案】3
【分析】如图作PQ⊥AB于Q，PR⊥BC于R．由△QPE∽△RPF，推出==2，可得PQ=2PR=2BQ，由PQ∥BC，可得AQ：QP：AP=AB：BC：AC=3：4：5，设PQ=4x，则AQ=3x，AP=5x，BQ=2x，可得2x+3x=3，求出x即可解决问题．
【详解】如图，作PQ⊥AB于Q，PR⊥BC于R．
∵∠PQB=∠QBR=∠BRP=90°，∴四边形PQBR是矩形，∴∠QPR=90°=∠MPN，∴∠QPE=∠RPF，∴△QPE∽△RPF，∴==2，∴PQ=2PR=2BQ．
∵PQ∥BC，∴AQ：QP：AP=AB：BC：AC=3：4：5，设PQ=4x，则AQ=3x，AP=5x，BQ=2x，∴2x+3x=3，∴x=，∴AP=5x=3．故答案为3．
【点睛】本题考查了相似三角形的判定和性质、勾股定理、矩形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考常考题型．
9．（2023年福建泉州中考数学模拟试卷）如图，在Rt△ABC中，∠A=90°，AB=12，AC=16，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°．
（1）求ED、EC的长；（2）若BP=2，求CQ的长；（3）若线段PQ与线段DE的交点为F，当△PDF为等腰三角形时，求BP的长．
【答案】（1）DE=，CE=；（2）CQ的长为11或14；（3）BP=或．
【详解】分析：（1）先根据勾股定理求得BC的长，再结合点D为BC的中点可得CD的长，然后证得△ABC∽△DEC，根据相似三角形的性质即可求得结果；（2）分点P在AB边上和点P在AB的延长线上两种情况求解即可；（3）先证得△PDF∽△CDQ，因△PDF为等腰三角形 可得△CDQ为等腰三角形，再分CQ=CD、QC=QD和DC=DQ三种情况，根据等腰三角形的性质求解即可.
详解：（1）∵∠A=90°，AB=12，AC=16，
∴根据勾股定理得到，BC==20，∴CD=BC=10，
∵DE⊥BC，∴∠A=∠CDE=90°，∠C=∠C，∴△CDE∽△CAB，
∴DE：AB=CE：CB=CD：CA，即DE：12=CE：20=10：16，∴DE=，CE=；
（2）分两种情况考虑：如图，∵△CDE∽△CAB，∴∠B=∠DEC，
∵∠PDQ=90°，∴∠QDC+∠PDB=90°，
∵∠QDC+∠EDQ=90°，∴∠EDQ=∠PDB，∴△PBD∽△QED，
∴=，即=，∴EQ=，∴CQ=CE﹣EQ=﹣=11；如图2，
∵∠B=DEC，∴∠PBD=∠QED，∵∠PDQ=90°∴∠BPD+∠QDB=90°，
∵∠QDE+∠QDB=90°，∴∠BDP=∠QDE，∴△PBD∽△QED，
∴=，即=，∴EQ=，∴CQ=+=14，则CQ的长为11或14；
（3）∵线段PQ与线段DE的交点为点FF，∴点P在边AB上，
∵△BPD∽△EQD，∴====，若设BP=x，则EQ=x，CQ=﹣x，
∵ct∠QPD==，ctC===，∴∠QPD=∠C，
∵∠PDE=∠CDQ，∴△PDF∽△CDQ，∵△PDF为等腰三角形，∴△CDQ为等腰三角形，
①当CQ=CD时，可得：﹣x=10，解得：x=；
②当QC=QD时，过点Q作QM⊥CB于M，如图3所示，∴CM=CD=5，
∵cs∠C====，∴CQ=，∴﹣x=，解得：x=；

③当DC=DQ时，过点D作DN⊥CQ于N，如图4所示，∴CQ=2CN，
∵cs∠C===，∴CN=8，∴CQ=16，∴﹣x=16，解得：x=﹣（舍去），
∴综上所述，BP=或．
点睛：本题考查了直角三角形的性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，分类讨论思想在解实际问题的运用，等腰三角形的性质的运用，三角函数值的运用，解答时运用三角函数值求证三角形的角相等是难点，证明三角形相似是关键．
10．（2022春·四川达州·九年级专题练习）已知，在中，．
（1）如图1，已知点D在边上，，连结．试探究与的关系；
（2）如图2，已知点D在下方，，连结．若，，，交于点F，求的长；（3）如图3，已知点D在下方，连结、、．若，，，，求的值．
【答案】（1），理由见详解；（2）；（3）
【分析】（1）由题意易得，则易证，然后根据全等三角形的性质可求解；
（2）过点A作AH⊥BC于点H，由题意易得，，然后可得，进而根据勾股定理可得，设，则，易得，则有，所以，最后问题可求解；
（3）将△ABD绕点A逆时针旋转90°得到△ACG，过点A作AP⊥BC于点P，作DT⊥BC于点T，分别过点G作GM⊥BC，GN⊥AP，交BC的延长线于点M，交AP于点N，由题意易得，，则有，然后可得，设，，进而根据勾股定理可求解x的值，然后根据三角函数可进行求解．
【详解】解：（1），理由如下：
∵，∴，∴，
∵，∴，∴；
（2）过点A作AH⊥BC于点H，如图所示：
∵，∴△BAC是等腰直角三角形，∵，∴，
∵，∴，∴，
∵，∴，
∵，∴，∵，∴，
∵，∴，
设，则，∴，
∴，∴，解得：，∴AF=5；
（3）将△ABD绕点A逆时针旋转90°得到△ACG，过点A作AP⊥BC于点P，作DT⊥BC于点T，分别过点G作GM⊥BC，GN⊥AP，交BC的延长线于点M，交AP于点N，如图所示：
∵，，∴△BAC是等腰直角三角形，
∴，，∴，
∵，∴，由旋转的性质可得，
∴，∴，∴，
∵GM⊥BC，GN⊥AP，AP⊥BC，∴四边形GMPN是矩形，
∴，设，
∴，
在Rt△ANG中，，
∵，∴，
化简得：，解得：，
∵，∴当时，易知与相矛盾，
∴，∴，∴，
∴，∴在Rt△DTC中，，∴．
【点睛】本题主要考查三角函数、相似三角形的性质与判定、旋转的性质及勾股定理，熟练掌握三角函数、相似三角形的性质与判定、旋转的性质及勾股定理是解题的关键．
11．（2023辽宁铁岭市中考模拟）如图，中，，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且．
（1）如图1，当时，线段AG和CF的数量关系是 ．
（2）如图2，当时，猜想线段AG和CF的数量关系，并加以证明．
（3）若，，，请直接写出CF的长．
【答案】（1）；（2），理由见解析；（3）2.5或5
【分析】（1）如图1，连接AE，根据线段垂直平分线的性质得到，根据等腰直角三角形的性质得到，，，根据全等三角形的性质即可得到结论；
（2）如图2，连接AE，根据等腰三角形的性质和三角形的内角和得到，根据线段垂直平分线的性质得到，求得，根据相似三角形的性质得到，解直角三角形即可得到；（3）①当G在DA上时，如图3，连接AE，根据线段垂直平分线的性质得到，，由三角函数的定义得到，根据相似三角形的性质得到，过A作于点H由三角函数的定义即可得到结论．②当点G在BD上，如图4，方法同（1）．
【详解】解：（1）相等，理由：如图1，连接AE，
∵DE垂直平分AB，，，，
，，，
，，
，，
，，；故答案为；
（2），理由：如图2，连接AE，，，，
∵DE垂直平分AB，，，，，
，，
，，，
，在中，，，，；
（3）①当G在DA上时，如图3，连接AE，∵DE垂直平分AB，，，
，，，，
，，，
，，
，，，
，过A作于点H，，，
，，，，
，，；
②当点G在BD上，如图4，同（1）可得，，，
，，，
综上所述，CF的长为2.5或5．
【点睛】本题考查了等腰三角形的性质，线段垂直平分线的性质，全等三角形的判定和性质，相似三角形的判定和性质，正确的作出辅助线是解题的关键．
12．（2023西南交通大学附属中学九年级月考）在中，，，，点为边的中点，交边于点，点为直线上的一动点，点为直线上的一动点，且．
（1）求、的长．（2）若，求的长．（3）记线段与线段的交点为点，若为等腰三角形，求的长．
【答案】（1），；（2）或；（3）或
【分析】（1）由勾股定理求得BC=10．通过“两角法”证得△CDE∽△CAB，则对应边成比例DE：AB=CE：CB=CD：CA，由此可以求得DE、CE的值；（2）如图2，当P点在AB上时，由∠PDQ=90°就可以得出∠2=∠4，就可以证明△PBD∽△QED，就可以EQ的值，从而求得CQ的值；如图2-1，当P点在AB的延长线上时，证明△PBD∽△QED，由相似三角形的性质就可以求出结论；
（3）如图3，4，5由条件可以求出△BPD∽△EQD，就有，设BP=x，则EQ=，CQ=，由三角函数值可以得出△PDF∽△CDQ．由△PDF为等腰三角形就可以得出△CDQ为等腰三角形，根据等腰三角形的性质，分三种情况讨论就可以求出结论．
【详解】解：（1）如图，∵，，，

∴根据勾股定理得到，∴．
∵．∴，
∴∴，
即∴，．
（2）如图，∵，∴．
∵∴．∵∴，∴，
∴，∴，∴，∴．
如图，∵，∴．∵∴．
∵∴，∴
∴，∴，∴，∴故或．
（3）∵线段与线段的交点为点，∴点在边上
∵∴．
若设，则，．
∵，，∴
∵，∴．
∵为等腰三角形，∴为等腰三角形．
①当时，可得：，解得：．
②当时，过点作于，∴．
∵，∴，∴．∴解得：
③当时，过点作于，∴．∵∴，
∴，∴，∴解得：（舍去）．∴综上所述，或．

【点睛】本题考查了直角三角形的性质的运用，勾股定理的运用，相似三角形的判定及性质的运用，分类讨论思想在解实际问题的运用，等腰三角形的性质的运用，三角函数值的运用，解答时运用三角函数值求证三角形的角相等是难点，证明三角形相似是关键．
13．（2022秋·山西吕梁·九年级校考阶段练习）综合与实践
问题情境：在中，．点在斜边上运动，过点作射线，分别与边交于点．
猜想证明：（1）当点在斜边的中点处时，

①如图（1），在旋转过程中，当点时，与的数量关系是______，_______．
②当旋转到如图②所示的位置时，的值是否发生变化？若不变，请证明；若变化，请说明理由．
③如图③，在旋转过程中，当时，直接写出线段的长_______；
类比探究（2）当点在斜边上运动时，
①如图④，当点运动到时，_______；
②如图⑤，连接，当是等腰三角形时，求的长．
【答案】（1）①，；②不变化，证明见解析；③；（2）①；②
【分析】（1）①证明四边形是矩形，求出，然后根据平行线分线段成比例定理可得，进而可得答案；
②如图②，过点D作，证明，结合（1）的结论即可解答；
③如图③，过点D作，同理可证：，设，然后根据相似三角形的性质结合①②列出方程求解即可；
（2）①如图④，过点D作，利用三角函数求出，证明，再根据相似三角形的性质即可求出答案；
②当是等腰三角形时，由于，故只有，如图⑤，过点D作，证明，得出，然后设，利用三角函数分别用含x的代数式表示出，进而可得关于x的方程，求解x即可解决问题．
【详解】解：（1）①如图①，在中，∵，∴，
∵点在斜边的中点，∴，
∵，，，∴四边形是矩形，
∴，，，
∴，∴，
∴，，故答案为：，；

②的值不发生变化，；
证明：如图②，过点D作，垂足分别为点G、H，则，
同①的证明可得：，，
∵，∴，∴，∴；
③如图③，过点D作，垂足分别为点G、H，
同理可证：，∴，设，
由①的结论可得：，
∴，∴，解得：，即；
（2）①如图④，过点D作，垂足分别为点G、H，
当时，即，
∵，∴，，
∵，，∴，∴，∴；

②当是等腰三角形时，由于，∴只有，
如图⑤，过点D作，垂足分别为点G、H，则，，
∵，∴，
∴，∴，设，
∵，，∴，
∵，∴，解得，∴．
【点睛】本题是三角形综合题，主要考查了勾股定理、矩形的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质以及解直角三角形等知识，具有一定的综合性，熟练掌握相关图形的性质定理、正确添加辅助线是解题的关键．
14．（2023秋·山西忻州·九年级校考期末）综合与实践
问题情境：在学习了三角形的相似后，同学们开始了对不同三角形中的相似模型的探究．
猜想推理：

（1）如图1，在等边中，D为边上一点，E为边上一点，，，，则______．
问题解决：（2）如图2，是等边三角形，D是的中点，射线，分别交，于点E，F，且，求证：．
（3）如图3，，，，D是的中点，射线，分别交，于点E，F，且，求的值．
【答案】（1）；（2）见解析；（3）
【分析】（1）首先求出，证明，得到，即可求出结果；
（2）连接，过D作于M，作于N，根据证明，再根据全等三角形的性质可得；
（3）过点分别作于，于，根据勾股定理及中位线的性质可得，，根据矩形的性质可得，最后由相似三角形的判定与性质可得答案．
【详解】解：（1）∵在等边中，，，，
∴，
∵，，
∴，∴，∴，即，∴；
（2）如图，连接，过D作于M，作于N，
∵是等边三角形，D为的中点，
∴是的平分线，，∴，，
又∵，∴，∴，
∴在与中，，∴，∴；

（3）过点分别作于，于，

在中，，是的中点，，
，，，，，
是的中点，是的中位线，是的中位线，，，
四边形为矩形，，，
，，
，，．
【点睛】本题考查了三角形综合题．需要掌握等边三角形的性质，全等三角形的判定与性质，相似三角形的判定和性质，关键是找到图中关键的相似和全等三角形，比较典型，但有点难度．
15．（2023广东深圳三模试题）（1）【探究发现】如图1，正方形的对角线相交于点，在正方形绕点旋转的过程中，边与边交于点，边与边交于点．证明：；

（2）【类比迁移】如图2，矩形的对角线相交于点，且，．在矩形绕点旋转的过程中，边与边交于点，边与边交于点．若，求的长；

（3）【拓展应用】如图3，四边形和四边形都是平行四边形，且，，，是直角三角形．在绕点旋转的过程中，边与边交于点，边与边交于点．当与重叠部分的面积是的面积的时，请直接写出的长．

【答案】（1）见解析（2）（3）
【分析】（1）根据正方形的性质和全等三角形的性质，找相等的边和角证全等即可；
（2）过点作的平行线交于点、交于点，过点作垂线交于点，构造相似三角形和，列比例式求解算出，最后根据计算即可；
（3）过点作的垂线交于点，根据勾股定理算出，根据已知条件观察推理出，，结合与重叠部分的面积是的面积的，设列方程求出，最后根据勾股定理求出即可．
【详解】（1）正方形的对角线相交于点，在正方形绕点旋转的过程中，边与边交于点，边与边交于点
，，，
，即，
在和中，；
（2）如图，过点作的平行线交于点、交于点，过点作垂线交于点，

四边形和四边形都是矩形，，，，
，，，
，
，，
，，，即，，
；
（3）如图，过点作的垂线交于点，

设，则，
设，则，
，，，
又，，
，，四边形和四边形都是平行四边形，是直角三角形
∴，(有公共角且都有直角)，
，∴，∵，即，
∴，，设，则，
∵，即，∴，
与重叠部分的面积是的面积的，平行四边形对角线平分平行四边形的面积，
，即，
∴，即，∴，
∴，∴．
【点睛】本题综合考查了全等三角形的证明、勾股定理、特殊四边形（平行四边形、矩形、正方形）的性质、相似三角形，综合性强，熟练掌握相关知识、结合图象分析是解题的关键．