山西省晋中市平遥县2022-2023学年七年级下学期期中教学质量监测数学试卷(含解析)

这是一份山西省晋中市平遥县2022-2023学年七年级下学期期中教学质量监测数学试卷(含解析)，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列运算正确的是( )
A. B. C. D.
2. 下列各图中，与是对顶角的是( )
A. B.
C. D.
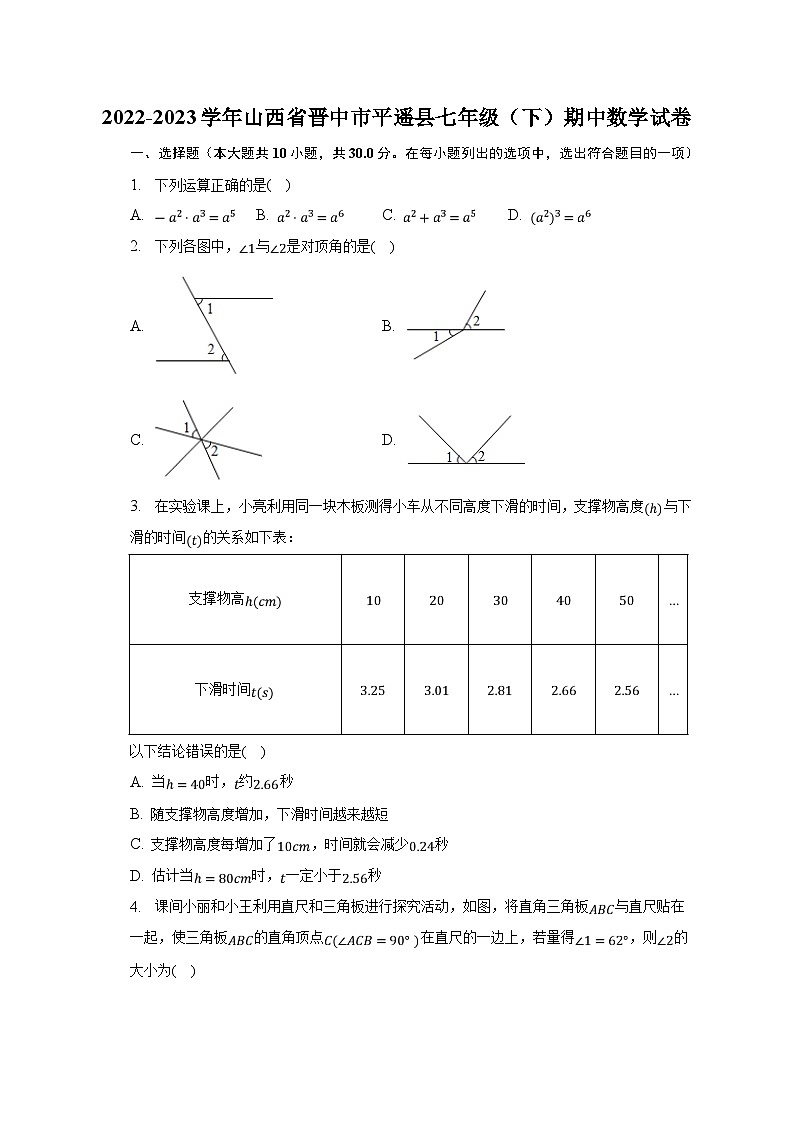
3. 在实验课上，小亮利用同一块木板测得小车从不同高度下滑的时间，支撑物高度与下滑的时间的关系如下表：
以下结论错误的是( )
A. 当时，约秒
B. 随支撑物高度增加，下滑时间越来越短
C. 支撑物高度每增加了，时间就会减少秒
D. 估计当时，一定小于秒
4. 课间小丽和小王利用直尺和三角板进行探究活动，如图，将直角三角板与直尺贴在一起，使三角板的直角顶点在直尺的一边上，若量得，则的大小为( )
A. B. C. D.
5. 如图，是一条水平线，把一头系着小球的线一端固定在点，小球从到从左向右摆动，在这一过程中，系小球的线在水平线下方部分的线段长度的变化是( )
A. 从大变小
B. 从小变大
C. 从小变大再变小
D. 从大变小再变大
6. 研究表明，当前变异新冠病毒毒性逐渐减弱，正确佩戴口罩仍很必要某新型冠状病毒体大小约为微米，而口罩能过滤微米的颗粒，并不能将病毒过滤，口罩的作用是阻挡病毒传播的“载体”，而非直接挡住病毒微米就是米那么微米用科学记数法表示为( )
A. 米B. 米C. 米D. 米
7. 在进行整式乘法运算训练时，李明出了一道题：要求计算得到的多项式不含、的一次项，其中，是常数，请你分析并求出的值为( )
A. B. C. D.
8. 如图，直线，点，分别在直线．和直线上，点在两条平行线之间，和的角平分线交于点，已知，则的度数为( )
A.
B.
C.
D.
9. 如图，在某个底面积为盛水容器内，有一个实心圆柱体铁块，现在匀速持续地向容器内注水，容器内水的高度和注水时间之间的关系满足如图中的图象，则水流速度是．( )
A. B. C. D.
10. 如图，两个正方形边长分别为，，已知，，则阴影部分的面积为( )
A.
B.
C.
D.
二、填空题（本大题共5小题，共15.0分）
11. 如果一个角的余角是，那么这个角的补角的度数是______ ．
12. 如图，是小明学习三线八角时制作的模具，经测量，要使木条与平行，则的度数必须是______度．
13. 新冠疫情复工复产后，商场开展促销活动已知某种商品的售价为元件，规定凡购买该商品超过件，则超出的部分按照售价的折付款若一位顾客购买了件，需付款元，则与间的关系式是______ ．
14. 定义一种新运算，若，则，例，已知，则的值为______．
15. 将一副三角板按如图放置，则下列结论：
；如果，则有；；如果，必有其中正确的有______填写序号
三、解答题（本大题共7小题，共55.0分。解答应写出文字说明，证明过程或演算步骤）
16. 本小题分
计算：
．
．
17. 本小题分
王老师给学生出了一道题：
求的值，其中，．
同学们看了题目后发表不同的看法．
小明说：“条件是多余的”
小亮说：“不给这个条件，就不能求出结果，所以不多余”
你认为他俩谁说的有道理？为什么？
18. 本小题分
如图为一位旅行者在早晨时从城市出发到郊外所走的路程单位：千米与时间单位：时的变量关系的图象．根据图象回答问题：
在这个变化过程中，自变量是______ ，因变量是______ ．
时，时，时所走的路程分别是多少？
他休息了多长时间？
他从休息后直至到达目的地这段时间的平均速度是多少？
19. 本小题分
用边长分别为，的两个正方形和长宽分别为，的两个长方形按如图摆放可拼成一个大正方形，用两种不同的方法可以表示图中阴影部分的面积和．
请你用一个等式表示，，之间的数量关系______ ．
根据中的数量关系，解决如下问题：
已知，，求的值；
已知，求的值．
20. 本小题分
如图所示，，直线分别交、于点、，是的平分线．

如果是的平分线，如图试判断并证明和的位置关系；
证明：，
______ 两直线平行，同位角相等．
是的平分线，
______ ______ ．
是的平分线．
______ ______ ．
等量代换
和的位置关系是______ ，______
如果是的平分线，如图中的结论还成立吗？不必证明
如果是的平分线，如图中的结论还成立吗？如果不成立，与又有怎样的位置关系？请直接写出你的猜想不必证明．
21. 本小题分
阅读探究题：
【阅读材料】
比较两个底数大于的正数幂的大小，可以在底数或指数相同的情况下，比较指数或底数的大小，
如：，．
在底数或指数不相同的情况下，可以化相同，进行比较，如：与，
解：，
，
．
．
上述求解过程中，运用了哪一条幂的运算性质______
A.同底数幂的乘法
B.同底数幂的除法
C.幂的乘方
D.积的乘方
类比解答：比较，的大小．
拓展提高：比较，，的大小．
22. 本小题分
问题情境：
如图，，，求的度数小明的思路是：过作，通过平行线性质，可得．
问题解决：

如图，，直线分别与、交于点、，点在直线上运动，当点在线段上运动时不与点、重合，，，判断、、之间的数量关系并说明理由；
在的条件下，如果点在线段或的延长线上运动时请直接写出、、之间的数量关系；
如图，，点是、之间的一点点在点、右侧，连接、，和的平分线交于点若，请结合中的规律，求的度数．
答案和解析
1.
解：，故A不符合题意；
B.，故B不符合题意；
C.与不能合并，故C不符合题意；
D.，故D符合题意；
故选：．
根据合并同类项，幂的乘方与积的乘方，同底数幂的乘法运算法则进行计算即可．
本题考查了合并同类项，幂的乘方与积的乘方，同底数幂的乘法，熟练掌握它们的运算法则是解题的关键．
2.
解：、与不是对顶角，故此选项不符合题意；
B、与不是对顶角，故此选项不符合题意；
C、与是对顶角，故此选项符合题意；
D、与不是对顶角，故此选项不符合题意；
故选：．
3.
解：由表格中下滑时间随支撑物高度的对应值可得，当时，下滑的时间为秒，因此选项A不符合题意；
B.由表格中下滑时间随支撑物高度的变化情况可知，随支撑物高度增加，下滑时间越来越短，因此选项B不符合题意；
C.由表格中下滑时间随支撑物高度的对应值可知，支撑物高度每增加了，时间不都减少秒，因此选项C符合题意；
D.由表格中下滑时间随支撑物高度的变化趋势可知，当时，一定小于秒，因此选项D不符合题意；
故选：．
根据表格中下滑时间随支撑物高度的变化规律逐项进行判断即可．
本题考查函数的表示方法，理解表格中下滑时间随支撑物高度的变化关系是正确判断的关键．
4.
解：如图，，
，
，即，
，
，
，
故选：．
根据平行线的性质以及图形中角的和差关系进行解答即可．
本题考查平行线的性质，掌握平行线的性质是正确解答的前提．
5.
解：根据题意可知：小球在以点为圆心，以长为半径的圆弧上运动，
如图：过点作与点，交弧于点，

，，
，
即，
故系小球的线在水平线下方部分的线段长度的变化是从小变大再变小，
故选：．
根据题意可知：小球在以点为圆心，以长为半径的圆弧上运动，据此即可解答．
本题考查了垂线段最短，圆的相关概念，理解垂线段最短的性质是解决本题的关键．
6.
解：微米米米米．
故选：．
科学记数法的表现形式为的形式，其中，为整数，确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同，当原数绝对值大于等于时，是正整数，当原数绝对值小于时，是负整数．
本题考查了科学记数法的表示方法，科学记数法的表现形式为的形式，其中，为整数，表示时关键是要正确确定的值以及的值．
7.
解：


因为这个多项式不含一次项，
所以，，
解得，．
所以
故选：．
多项式乘多项式法则，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．结果中不含一次项和二次项，则说明这两项的系数为，建立关于，等式，求解得到、的值即可解决问题．
本题考查了整式的混合运算，多项式乘以多项式，根据不含某一项就是这一项的系数等于列式求解、的值是解题的关键．
8.
解：过点作，

，，
，
，
，
和的角平分线交于点，
，，
，
，
故选：．
过点作，根据平行线的性质和角平分线的定义解答即可．
本题考查了平行线的性质，平角的定义，是基础题，熟记概念并准确识图是解题的关键．
9.
解：根据函数图象得到圆柱形容器的高为，实心圆柱体铁块的高度为，
水满过实心圆柱体铁块需注满，“几何体”上面的空圆柱形容器需，
设匀速注水的水流速度为，则：
，
解得，
即匀速注水的水流速度为．
故选：．
根据图象，分两个部分：满过实心圆柱体铁块需，注满“几何体”上面的空圆柱形容器需，再设匀速注水的水流速度为，根据圆柱的体积公式列方程，再解方程．
本题考查了函数的图象，把分段函数图象中自变量与对应的函数值转化为实际问题中的数量关系，然后运用方程的思想解决实际问题．
10.
解：根据题意可得，


，
把，代入上式，
则．
故选：．
根据题意可得，阴影部分的面积等于边长为的正方形面积减去边长为的等腰直角三角形面积，再减去边长为和的直角三角形面积，即可得，根据完全平方公式的变式应用可得，代入计算即可得出答案．
本题主要考查了完全平方公式的几何背景，熟练掌握完全平方公式的变式应用进行求解是解决本题的关键．
11.
解：一个角的余角是，则这个角为，
这个角的补角的度数是．
故答案为：．
先根据题意求出这个角的度数，再根据补角的定义求解即可．
本题考查了余角和补角的定义，属于基础题，解题时牢记定义是关键，难度一般．
12.
解：如图，
，
，
要使与平行，则，
．
故答案为：．
先求出的对顶角的度数，再根据同旁内角互补，两直线平行解答．
本题主要考查了平行线的判定，熟练掌握平行线的判定方法是解题的关键，
13.
解：依题意，，
；
故答案为：．
根据题意，付款金额等于件的全额费用加上超出部分的六折的费用，即可求解．
本题考查了列函数关系式，理解题意是解题的关键．
14.
解：设，，
依题意，，
．
，



．
故答案为：．
设，，根据新运算定义用、表示，得方程，求出的值．
本题考查了幂的乘方、积的乘方等知识点，理解并运用新运算的定义是解决本题的关键．
15.
解：，，
，故正确；
，
，
又，
，
，故正确；
，，
故正确；
，
，
，
，
，故正确；
故答案为：．
先根据余角的概念和同角的余角相等判断；再根据平行线的判定定理判断；然后根据角的和差判断；最后根据平行线的判定与性质判断．
本题考查的是平行线的性质和余角、补角的概念，掌握平行线的性质定理和判定定理是解题的关键．
16.解：原式
；
原式

．
首先计算负整数指数幂，有理数的乘方和零指数幂，然后计算加法即可；
利用平方差公式及完全平方公式进行运算较简便．
本题主要考查负整数指数幂，有理数的乘方，零指数幂和整式的混合运算，解答的关键是对相应的运算法则的掌握．
17.解：小明说的有道理，
理由：


，
化简后的结果不含，
小明说的有道理．
利用平方差公式，完全平方公式，多项式除以单项式的法则，进行计算即可解答．
本题考查了整式的混合运算化简求值，平方差公式，完全平方公式，准确熟练地进行计算是解题的关键．
18.时间；路程
解：由图象可得，时间是自变量，路程是因变量；
故答案为：时间；路程；
由图可知：时，时，时所走的路程分别是，，；
根据图象可得，该旅行者休息的时间为：小时；
根据图象得：．
根据自变量是横轴表示的量，因变量是纵轴表示的量，解答即可．
由图象看相对应的值即可．
由图象可知，休息时，时间在增多，路程没有变化，表现在函数图象上是与轴平行的线段．
根据这段时间的平均速度这段时间的总路程这段时间，算出即可．
本题主要考查了分段函数的图象，正确理解函数的图象所表示的意义，能够通过图象得到函数自变量和因变量的变化关系；注意休息时表现在函数图象上是与轴平行的线段．
19.
解：方法一：阴影部分是两个正方形的面积和，即；
方法二：阴影部分也可以看作边长为的面积，减去两个长为，宽为的长方形面积，即，
由两种方法看出，
故答案为：；
，
，
，
，
即；
，
；
设，，
则，，
，
即，
，
．
阴影部分是两个正方形的面积和，阴影部分也可以看出大正方形的面积减去两个长方形的面积即可得出答案；
先根据完全平方公式求出，再根据作答即可；
设，，先根据题意求出的值，再用完全平方公式计算即可．
本题考查了完全平方公式，熟练掌握完全平方公式的应用是解题的关键．
20. 平行 同位角相等，两直线平行
解：，
两直线平行，同位角相等．
是的平分线，
．
是的平分线．
．
等量代换
和的位置关系是平行，同位角相等，两直线平行．
故答案为：，，，，，同位角相等，两直线平行；
成立；
证明，
，
是的平分线，
．
是的平分线．
．
，
和的位置关系是平行，
不成立；垂直；
证明：
设，相交于点，
，
两直线平行，同旁内角互补．
是的平分线，
．
是的平分线．
．
，
，
和的位置关系是垂直．
根据角平分线的性质及平行线的性质求解；
根据角平分线的性质及平行线的性质求解；
根据角平分线的性质、平行线的性质及垂直的意义求解；
本题考查了平行线的性质，掌握平行线的性质及角平分线分性质是解题的关键．
21.
解：上述求解过程中，运用了幂的乘方的运算性质，
故答案为：；
，，
，
；
，，，
，
．
根据幂的乘方运算法则判断即可；
根据幂的乘方运算法则解答即可；
根据幂的乘方运算法则解答即可．
本题考查幂的乘方与积的乘方、有理数大小比较，解答本题的关键是明确有理数大小的比较方法．
22.解：如图，过点作，
，
，
，，
．
如图，在的条件下，如果点在线段的延长线上运动时，
，，
，
，，
，
；
如图，在的条件下，如果点在线段的延长线上运动时，
，，
，
，，
，
；
如图，过点，分别作，，
，
，
，，
，
，
平分，平分，
，，
，
，
，，
，
．
过点作，根据平行线的判定与性质即可求解；
分点在线段或的延长线上运动两种情况，根据平行线的判定与性质及角的和差即可求解；
过点，分别作，，根据平行线的判定与性质及角的和差即可求解．
此题考查了平行线的判定与性质，添加辅助线将两条平行线相关的角联系到一起是解题的关键．
支撑物高
下滑时间