高考数学第一轮复习复习第8节　函数与方程（讲义）

这是一份高考数学第一轮复习复习第8节　函数与方程（讲义），共20页。

1.结合学过的函数图象,了解函数零点与方程解的关系.
2.结合具体连续函数及其图象的特点,了解函数零点存在定理,并能简单应用.
3.了解用二分法求方程的近似解的步骤.
1.函数的零点
(1)函数零点的定义:使f(x)=0的实数x叫做函数y=f(x)的零点.
(2)三个等价关系:方程f(x)=0有实数解⇔函数y=f(x)有零点⇔函数y=f(x)的图象与x轴有公共点.
函数的零点不是一个点,而是一个实数.该实数是函数图象与x轴交点的横坐标.
2.函数零点存在定理
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的解.
函数f(x)在(a,b)上连续且单调,而且f(a)f(b)<0,则f(x)在(a,b)上有且仅有一个零点.
3.二分法
对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
用二分法求方程的近似解应具备两个条件,一是方程对应的函数在零点附近连续不断,二是该零点左、右的函数值异号.
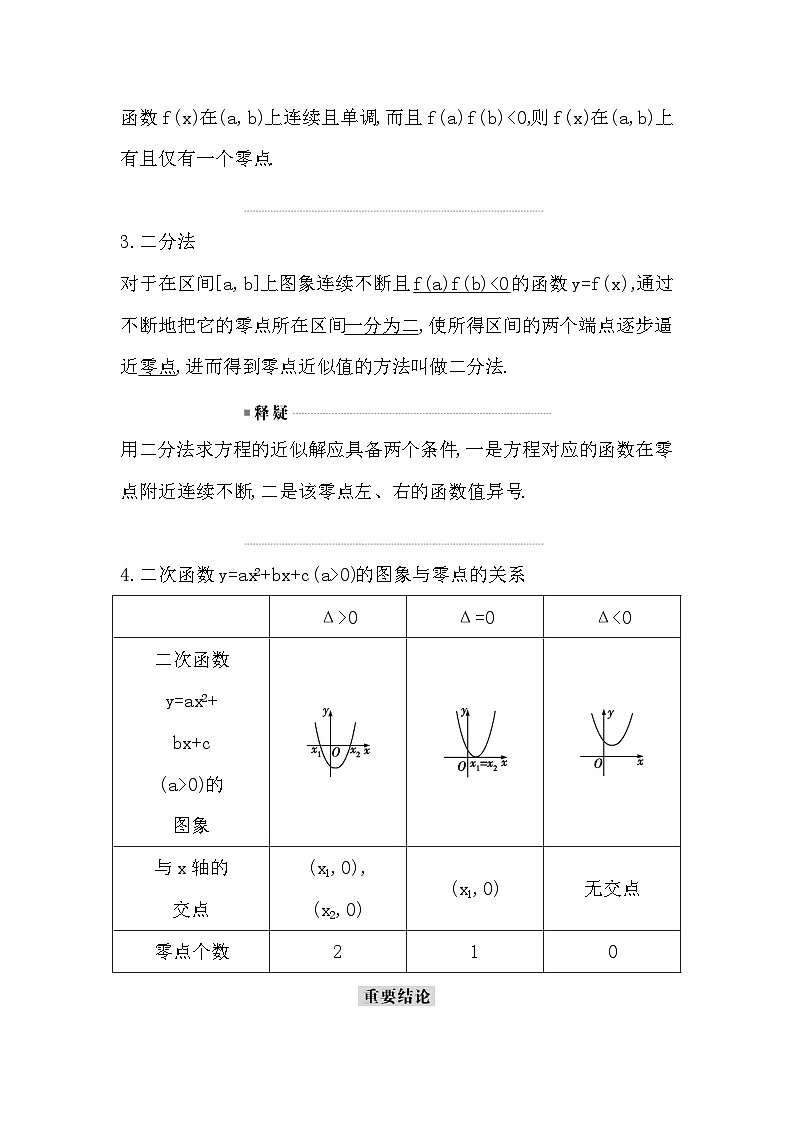
4.二次函数y=ax2+bx+c(a>0)的图象与零点的关系
1.若函数y=f(x)在闭区间[a,b]上的图象是一条连续不断的曲线,并且有f(a)·f(b)<0,则函数y=f(x)一定有零点.特别是,当y=f(x)在[a,b]上单调时,它仅有一个零点.
2.由函数y=f(x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出f(a)·f(b)<0,如图所示,所以f(a)·f(b)<0是y=f(x)在闭区间[a,b]上有零点的充分不必要条件.
1.(必修第一册P155 T2改编)函数y=f(x)的图象是一条连续不断的曲线,部分对应关系如表所示,则该函数的零点个数至少为( B )
A.2B.3C.4D.5
解析:由表可知,f(2)f(3)<0,f(3)f(4)<0,f(4)f(5)<0,所以函数f(x)在区间[1,6]上至少有3个零点.
2.(2022·湖北武汉期末)函数f(x)=3x+x-2的零点所在的一个区间是( A )
A.(0,1)B.(1,2)
C.(-2,-1)D.(-1,0)
解析:f(0)=-1,f(1)=2,故f(0)f(1)<0,由零点存在定理可知f(x)的零点所在的一个区间是(0,1).
3.已知函数f(x)=2x-1,x≤1,1+lg2x,x>1,则函数f(x)的零点为( D )
A.2B.-2,0C.12D.0
解析:当x≤1时,令f(x)=2x-1=0,解得x=0;当x>1时,令f(x)=1+lg2x=0,解得x=12(舍去).综上,函数的零点为0.
4.(2022·北京大兴区三模)已知a>0,若函数f(x)=x+a,x≤a,lnx+2,x>a有两个不同的零点,则a的取值范围是( A )
A.(0,1e2) B.(0,1)
C.(1e2,+∞)D.[1,+∞)
解析:x+a=0,x=-a则x=-a是函数f(x)的一个零点,
由ln x+2=0,解得x=1e2,
要使得f(x)有两个不同的零点,则a∈(0,1e2).
5.函数f(x)=x·2x-kx-2在区间(1,2)内有零点,则实数k的取值范围是 .
解析:令f(x)=0,
所以x·2x-kx-2=0,
即k=2x-2x,
即y=k与(x)=2x-2x,x∈(1,2)的图象有交点,
又(x)=2x-2x在(1,2)上单调递增,
且(1)=0,(2)=3,
所以0答案:(0,3)
函数零点存在定理的应用
1.(2022·天津一模)函数f(x)=ex+2x-6的零点所在的区间是( C )
A.(3,4)B.(2,3)
C.(1,2)D.(0,1)
解析:易知f(x)=ex+2x-6是R上的增函数,且f(1)=e-4<0,f(2)=e2-2>0,
所以f(1)f(2)<0,
所以f(x)的零点所在的区间是(1,2).
2.已知函数f(x)=lg2(x+1)+3x+m的零点在区间(0,1]上,则实数m的取值范围为( D )
A.(-4,0)
B.(-∞,-4)∪(0,+∞)
C.(-∞,-4]∪(0,+∞)
D.[-4,0)
解析:因为f(x)=lg2(x+1)+3x+m在区间(0,1]上单调递增,函数f(x)=lg2(x+1)+3x+m的零点在区间(0,1]上,所以f(0)<0,f(1)≥0,即m<0,lg22+3+m≥0,解得-4≤m<0.
3.(2023·湖南长沙调研)设函数f(x)=13x-ln x,则函数y=f(x)( D )
A.在区间(1e,1),(1,e)内均有零点
B.在区间(1e,1),(1,e)内均无零点
C.在区间(1e,1)内有零点,在区间(1,e)内无零点
D.在区间(1e,1)内无零点,在区间(1,e)内有零点
解析:令f(x)=0得13x=ln x.
作出函数y=13x和y=ln x的图象,如图所示,
显然y=f(x)在(1e,1)内无零点,在(1,e)内有零点.
4.已知函数f(x)=lgax+x-b(a>0,且a≠1).当2解析:因为2所以0lga3>1,
f(2)=lga2+2-b<3-b<0,
f(3)=lga3+3-b>4-b>0,
f(4)=lga4+4-b>0,
所以f(2)·f(3)<0,x0∈(2,3),所以函数f(x)的零点x0∈(n,n+1)时,n=2.
答案:2
确定函数零点所在区间的常用方法
(1)利用函数零点存在定理:首先看函数y=f(x)在区间[a,b]上的图象是否连续,再看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.
(2)数形结合法:通过画函数图象,观察图象与x轴在给定区间上是否有交点来判断.
函数零点个数的确定
[例1] (1)(2023·重庆模拟)已知函数f(x)=(12) x,x≤0,|lg2x|,x>0,则函数g(x)=f(x)-12的零点个数为( )
A.0B.1C.2D.3
(2)函数f(x)=4x-4x2的零点个数为( )
A.0B.1C.2D.3
(3)函数f(x)=2x|lg0.5x|-1的零点个数为( )
A.1B.2C.3D.4
解析:(1)令g(x)=f(x)-12=0,
即有f(x)=12,
当x≤0时,(12)x=12,解得x=1,不满足x≤0,所以无解;
当x>0时,|lg2x|=12,解得x=2或x=22.
所以g(x)的零点有2个.故选C.
(2)函数f(x)=4x-4x2的零点个数,即函数y=4x与函数y=4x2的图象的交点个数,根据指数函数与二次函数的性质可知,当x<0时,y=4x单调递增,值域为(0,1),y=4x2单调递减,值域为(0,+∞),两个函数有1个交点;
当x>0时,f(1)=41-4×12=0,f(2)=42-4×22=0,函数f(x)有2个零点.
综上所述,函数f(x)=4x-4x2的零点个数为3.故选D.
(3)函数f(x)=2x|lg0.5x|-1的零点个数⇔方程|lg0.5x|=12x=(12)x的根的个数⇔函数y=|lg0.5x|与y=(12)x的图象的交点个数,作出两个函数的图象如图所示,由图可知两个函数图象有两个交点.故选B.
求解函数零点个数的基本方法
(1)直接法:令f(x)=0,方程有多少个解,则f(x)有多少个零点;
(2)定理法:利用定理时往往还要结合函数的单调性、奇偶性等;
(3)图象法:一般是把函数拆分为两个简单函数,依据两函数图象的交点个数得出函数的零点个数.
[针对训练]
1.函数f(x)=2x+x3-2在区间(0,1)内的零点个数是( )
A.0B.1C.2D.3
解析:法一 因为f(0)·f(1)=(-1)×1=-1<0,函数在定义域上单调递增且连续,所以函数f(x)在区间(0,1)内有且只有1个零点.故选B.
法二 设y1=2x,y2=2-x3,在同一平面直角坐标系中画出两函数的图象如图所示,在区间(0,1)内,两图象的交点个数即为f(x)的零点个数.故函数f(x)在区间(0,1)内有且只有1个零点.故选B.
2.函数f(x)=x2+x-2,x≤0,-1+lnx,x>0的零点个数为( )
A.3B.2C.1D.0
解析:法一(直接法) 由f(x)=0得x≤0,x2+x-2=0或x>0,-1+lnx=0,
解得x=-2或x=e.因此函数f(x)共有2个零点.故选B.
法二(图象法) 函数f(x)的图象如图所示,由图象知函数f(x)共有2个零点.故选B.
函数零点的应用
根据零点的个数(或范围)求参数
[例2] (1)已知函数f(x)=ex,x≤0,ln2x,x>0,若函数F(x)=f(x)-a的两个零点分别在区间(-1,0)和(12,1)内,则实数a的取值范围为( )
A.(1e,ln 2)B.(0,1)
C.(ln 2,1)D.(1e,1)
(2)已知函数f(x)=ex-a,x≤0,2x-a,x>0(a∈R),若函数f(x)在R上有两个零点,则实数a的取值范围是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(-∞,1]
解析:(1)因为函数F(x)=f(x)-a的两个零点分别在区间(-1,0)和(12,1)内,所以F(-1)·F(0)<0,F(12)·F(1)<0,即(1e-a)(1-a)<0,(0-a)(ln2-a)<0,解得1e(2)画出函数f(x)的大致图象如图所示.因为函数f(x)在R上有两个零点,所以f(x)在(-∞,0]和(0,+∞)上各有一个零点.当x≤0时,f(x)有一个零点,需a≤1;当x>0时,f(x)有一个零点,需-a<0,即a>0.综上,0已知函数有零点求参数值或取值范围常用的方法和思路
(1)形如g(x)=f(x)-m的含参数函数零点问题可转化为f(x)=m求解.
(2)根据含参数的指数、对数、抽象函数的零点个数求参数的取值范围问题,若能够将参数分离,则常分离参数后求解,若分离参数后的不含参数的函数图象能够作出,则作出函数图象后利用数形结合思想求解.
求函数零点之和
[例3] 已知函数f(x)=lgx,x≥1,-lg(2-x),x<1,
g(x)=x3,则方程f(x)=g(x-1)的所有根的和等于( )
A.1B.2C.3D.4
解析:作出函数f(x)=lgx,x≥1,-lg(2-x),x<1,
g(x-1)=(x-1)3的图象如图所示.
函数y=f(x),y=g(x-1)的图象都关于点(1,0)对称,并且两个函数图象有三个交点,所以方程f(x)=g(x-1)的所有根的和为3.故选C.
求函数的多个零点(或方程的根以及直线y=m与函数图象的多个交点横坐标)的和时,常借助函数的性质(如函数本身关于点的对称、直线的对称等)求和.
二次函数的零点分布问题
[例4] 已知方程x2-mx-m+3=0.
(1)若方程不相等的两根都在[-4,0]内,求实数m的取值范围;
(2)若方程不相等的两根都小于5,求实数m的取值范围;
(3)若一根大于1,一根小于1,求实数m的取值范围.
解:令f(x)=x2-mx-m+3,则函数的图象是开口向上的抛物线.
(1)若x2-mx-m+3=0的不相等的两根都在[-4,0]内,
则Δ=m2+4m-12>0,-4解得m>2或m<-6,-8(2)x2-mx-m+3=0的两根都小于5,
则Δ=m2+4m-12>0,m2<5,f(5)=25-6m+3>0,
解得m<-6或2(3)若x2-mx-m+3=0的一根大于1,一根小于1,则f(1)=1-2m+3<0,
解得m>2.
若二次方程的根在一个区间上,则要考虑方程判别式Δ≥0,方程对应的二次函数图象的对称轴在该区间内,以及区间端点函数值的符号和开口方向;若二次方程的根在两个区间上,则只需要考虑区间端点的函数值符号和开口方向.
[针对训练]
1.已知函数f(x)=|lnx|,x>0,-x2-2x,x≤0,若g(x)=f(x)-a有4个零点,则实数a的取值范围是( )
A.(0,1)B.(0,1]
C.[0,1]D.[1,+∞)
解析:令g(x)=f(x)-a=0,得f(x)=a,
在同一平面直角坐标系中作出y=f(x),y=a的图象,如图所示.
由图象知,若g(x)=f(x)-a有4个零点,则实数a的取值范围是(0,1).故选A.
2.(2023·黑龙江大庆模拟)已知定义域为R的偶函数满足f(2-x)=f(x),当0≤x≤1时,f(x)=e1-x-1,则方程f(x)=1|x-1|在区间[-3,5]上所有解的和为( )
A.8B.7C.6D.5
解析:因为f(2-x)=f(x),
所以f(x)的图象关于直线x=1对称,
令h(x)=1|x-1|,则h(x)的图象关于直线x=1对称,
作出函数f(x)与h(x)在区间[-3,5]上的图象,如图所示,
由图可知,h(x)与f(x)的图象在区间[-3,5]上共有8个交点,且两函数关于直线x=1对称,
所以方程f(x)=1|x-1|在区间[-3,5]上所有解的和为4×2=8.故选A.
3.函数f(x)=x2-mx+9的两个不同的零点均大于1的一个充分不必要条件是( )
A.m∈(2,6)B.m∈(6,8)
C.m∈(6,10)D.m∈(6,+∞)
解析:因为函数f(x)=x2-mx+9的两个不同的零点均大于1,
所以f(1)>0,--m2>1,Δ>0,解得6因为(6,8)(6,10).故选B.
[知识链接]
函数的零点是命题的热点,常与函数的性质等相关问题交汇.对于判断形如f(g(x))的嵌套函数的零点个数或根据函数的零点求参数的取值范围时,可采用换元法,先令g(x)=t,求解当f(t)=0时t的值,然后根据函数g(x)的图象及性质确定当g(x)=t时,x的值的个数即为f(g(x))的零点个数.解答时注意数形结合,侧重对函数f(x)与g(x)图象性质的分析.
一、嵌套函数零点的个数问题
[典例1] (2022·湖南长沙质检)已知函数f(x)=ex,x<0,4x3-6x2+1,x≥0,其中e为自然对数的底数,则函数g(x)=3(f(x))2-10f(x)+3的零点个数为( )
A.4B.5C.6D.3
解析:当x≥0时,f(x)=4x3-6x2+1的导数为f′(x)=12x2-12x,
当01时,f′(x)>0,f(x)单调递增,
可得f(x)在x=1处取得最小值,最小值为-1,且f(0)=1,
作出函数f(x)的图象,如图所示,
g(x)=3(f(x))2-10f(x)+3,
可令g(x)=0,t=f(x),
可得3t2-10t+3=0,
解得t=3或13,
当t=13,即f(x)=13时,g(x)有3个零点;
当t=3时,可得f(x)=3有1个实根,即g(x)有1个零点.
综上,g(x)共有4个零点.故选A.
二、由嵌套函数零点的个数求参数的范围
[典例2] (2023·河南安阳模拟)已知函数f(x)=|2|x|-2|-1,且关于x的方程f2(x)+mf(x)+n=0有7个不同的实数解,则实数m,n满足( )
A.m>0,且n>0B.m<0,且n>0
C.0解析:令u=f(x),作出函数u=f(x)的图象如图所示,
由于方程u2+mu+n=0至多两个实根,
设为u=u1和u=u2,
由图象可知,直线u=u1与函数u=f(x)图象的交点个数可能为0,2,3,4,
由于关于x的方程f2(x)+mf(x)+n=0有7个不同实数解,
则关于u的二次方程u2+mu+n=0的一根为u1=0,则n=0,
则方程u2+mu=0的另一根为u2=-m,
直线u=u2与函数u=f(x)图象的交点个数必为4,则-1<-m<0,解得0所以0(1)解含参数的嵌套函数方程问题,应注意让参数的取值“动起来”,解题时要抓临界位置,动静结合.抓住两点:①转化换元;②充分利用函数的图象.
(2)作函数的图象必须关注其关键点(位置)和发展趋势、渐近线等,尤其当作图比例较大时,由于画的是局部图象,若关注度不够或疏忽,就会导致错误.
[拓展演练]
1.已知函数f(x)=x+1,x≤0,lg2x,x>0,则函数y=f(f(x))-1的零点个数为( )
A.3B.2C.0D.4
解析:y=f(f(x))-1=0,即f(f(x))=1.
当f(x)≤0时,f(x)+1=1,即f(x)=0时,此时lg2x=0,计算得出x=1,或者x+1=0,计算得出x=-1.
当f(x)>0时,lg2f(x)=1,即f(x)=2时,若x+1=2,计算得出x=1(舍去),若lg2x=2,计算得出x=4.综上所述,函数y=f(f(x))-1的图象与x轴的交点个数为3.故选A.
2.已知函数f(x)=-x,x≤0,-x2+2x,x>0,若方程f2(x)+bf(x)+18=0有六个相异实根,则实数b的取值范围为( )
A.(-2,-12)B.(-2,0)
C.(-98,-12)D.(-98,-22)
解析:函数f(x)的图象如图所示,
令t=f(x),则要使方程f2(x)+bf(x)+18=0有六个相异实根,只需要t2+bt+18=0在t∈(0,1)上有两个相异实根,则Δ=b2-12>0,0<-b2<1,1+b+18>0,
解得-98[例1] 已知x1是函数f(x)=2x+x-2的零点,x2是函数g(x)=lg2(x-1)+x-3的零点,则x1+x2的值为( )
A.17B.5C.12D.3
解析:由已知,可得f(x1)=2x1+x1-2=0,
所以2x1=2-x1,
所以x1是直线y=2-x与曲线y=2x的交点的横坐标,
g(x2)=lg2(x2-1)+x2-3=0,
则lg2(x2-1)=2-(x2-1),
则x2-1是直线y=2-x与曲线y=lg2x的交点的横坐标,如图所示,
y=lg2x与y=2x的图象关于直线y=x对称,
联立y=x,y=2-x,解得x=1,y=1,
所以直线y=x与直线y=2-x交于点C(1,1),
由图象知,点A,B关于点C对称,
所以x1+x2-1=2,所以x1+x2=3.故选D.
[例2] 已知函数f(x)=(12)x-|lg3(x-1)|有两个零点x1,x2,则( )
A.x1x2B.x1x2<1
C.x1x2=x1+x2
D.x1x2>x1+x2
解析:在同一平面直角坐标系下,作出函数y=(12)x与函数y=|lg3(x-1)|的图象如图所示,设x1∈(1,2),x2∈(2,+∞),
有(12) x1=-lg3(x1-1),
(12) x2=lg3(x2-1),
所以(12) x2-(12) x1=lg3(x2-1)+lg3(x1-1)=lg3[(x2-1)(x1-1)].
因为x1所以有lg3[(x2-1)(x1-1)]=lg3(x1x2-x1-x2+1)<0,即0所以x1x2[例3] 已知f(x)=|lnx|,x>0,2|x|,x≤0,则函数y=2f2(x)-3f(x)+1的零点个数是 .
解析:由2f2(x)-3f(x)+1=0得f(x)=12或f(x)=1,
作出函数y=f(x)的图象如图所示,
由图象知y=12与y=f(x)的图象有2个交点,y=1与y=f(x)的图象有3个交点.因此函数y=2f2(x)-3f(x)+1的零点有5个.答案:5Δ>0
Δ=0
Δ<0
二次函数
y=ax2+
bx+c
(a>0)的
图象
与x轴的
交点
(x1,0),
(x2,0)
(x1,0)
无交点
零点个数
2
1
0
x
1
2
3
4
5
6
y
126.1
15.15
-3.92
16.78
-45.6
-232.64