2025高考数学一轮考点突破训练第二章函数2.6函数的图象

这是一份2025高考数学一轮考点突破训练第二章函数2.6函数的图象，共9页。试卷主要包含了作图，识图，用图等内容，欢迎下载使用。

例1 作出下列函数的图象：
（1） ；
解：先作出 的图象，保留 图象中 的部分，再作出 的图象中 部分关于 轴的对称部分，即得 的图象.再向左、上分别平移1个单位长度可得，如图1实线部分.
图1
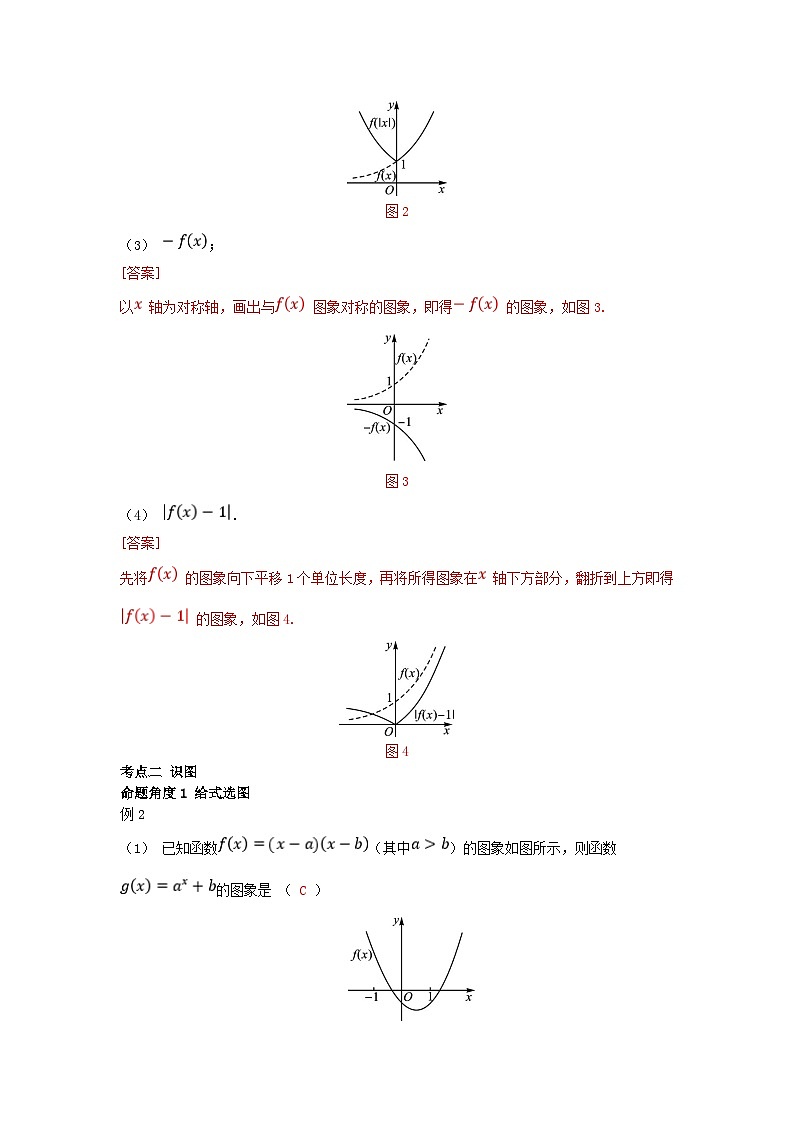
（2） ；
[答案]
将函数 的图象向左平移1个单位长度，再将 轴下方的部分沿 轴翻折上去，即可得到函数 的图象，如图2.
图2
（3） ；
[答案]
因为，所以函数图象可由 图象向右平移1个单位长度，再向上平移2个单位长度即得，如图3.
图3
（4） .
[答案]
其图象如图4.
图4
【点拨】 直接法作图，即根据函数的特征描出图象的关键点直接作出函数图象.图象变换法作图，即经过平移、翻折、对称、伸缩等得到函数图象，此时应注意平移变换与伸缩变换的顺序.
变式1 利用函数的图象，作出下列各函数的图象：
（1） ；
解：将 的图象向右平移1个单位长度，即得 的图象，如图1.
图1
（2） ；
[答案]
将 图象在 轴右侧的部分，以 轴为对称轴作出 轴左侧的图象，去掉原图象在 轴左侧部分,即得 的图象，如图2.
图2
（3） ；
[答案]
以 轴为对称轴，画出与 图象对称的图象，即得 的图象，如图3.
图3
（4） ．
[答案]
先将 的图象向下平移1个单位长度，再将所得图象在 轴下方部分，翻折到上方即得 的图象，如图4.
图4
考点二 识图
命题角度1 给式选图
例2
（1） 已知函数（其中）的图象如图所示，则函数的图象是 （ C ）
A. B.
C. D.
解：由题图，知，.所以 在 上单调递增，且.选项 满足要求.
故选 .
（2） [2022年全国甲卷]函数在区间,的图象大致为 （ A ）
A. B.
C. D.
解：令,,，
则，所以 为奇函数，排除，.
又当,时，,，
所以，排除.故选.
【点拨】 确定函数的图象主要用排除法.要抓住函数的性质，定性分析.①从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置.②从函数的单调性，判断图象的变化趋势.③从周期性，判断图象的循环往复.④从函数的奇偶性，判断图象的对称性.同时要善于抓住图象的特征，定量计算，即从函数的特征点入手，利用特征点、特殊值的计算分析等解决问题.
变式2
（1） 已知，则函数与函数的图象可能是②（填序号）．
解：因为，所以，即.则，.
当 时，，均是增函数，②正确.当 时，，均为减函数，①③④错误．或由 与 的图象关于直线 对称，判断②符合题意.故填②.
（2） [2021年天津卷]函数的图象大致为（ B ）
A. B.
C. D.
解：设，则函数 的定义域为，关于原点对称.又，所以函数 为偶函数，排除，.当 时，,，所以，排除.故选.
命题角度2 给图选式
例3 [2022年全国乙卷]如图是下列四个函数中的某个函数在区间的大致图象，则该函数是（ A ）
A. B. C. D.
解：设，则，故排除.
设，当,时，，
所以，故排除.
设，则，故排除.
故选.
【点拨】 由图选式，一般通过图象体现出的性质利用排除法筛选.与由式选图类似，主要用奇偶性、单调性、特值、极限等综合分析.
变式3 [2023年天津卷]函数的图象如图所示，则的解析式可能为（ D ）
A. B. C. D.
解：由题图，知函数 的图象关于 轴对称，其为偶函数，且.由 且定义域为，知 中函数为奇函数，排除.当 时，，，即,中 上函数值为正，排除.故选.
考点三 用图
例4
（1） 【多选题】某学习小组在研究函数的性质时，得出了如下结论，其中正确的是（ BCD ）
A. 函数的图象关于点中心对称B. 函数在上单调递增
C. 函数在的最大值为D. 方程有2个不同实数根
解：由 的路线，结合图象变换规则，可得 大致图象如图所示.
对于，由函数 是偶函数及图象知，函数 的图象不关于点 中心对称，故 错误.
对于，由图象知，函数 在 上单调递增,故 正确.
对于，由图知，函数 在 上单调递减，因此 时，,故 正确.
对于，当 时，,令，得，得.且由图象知，当 时，与 有一个交点，故 正确.故选 .
（2） 已知函数则不等式的解集是（ A ）
A. B. C. D.
解：分别作出函数 与 的图象，如图所示，
由图象，得不等式 的解集是.故选.
【点拨】①函数图象应用广泛，是研究函数性质不可或缺的工具.数形结合应以快、准为前提，充分利用“数”的严谨和“形”的直观，互为补充，互相渗透.②与指、对、幂混合型函数相关的不等式问题，常通过数形结合转化为函数图象的交点和在交点两侧图象的上、下位置关系来求解.
变式4
（1） 【多选题】关于函数，下列描述正确的是（ ABC ）
A. 函数在区间上单调递增
B. 函数的图象关于直线对称
C. 当时，方程有4个不同的实数根
D. 若，但，则
解：由题意，知.将函数 的图象关于 轴对称，可得 的图象，再将 的图象位于 轴下方的部分对折至 轴上方，可得 的图象，再将 的图象向右平移2个单位长度，可得 的图象，如图所示.
结合图象,可知函数 在区间 上单调递增，函数 的图象关于直线 对称，函数 的图象与 有且仅有4个交点，故,,正确.令,，则，但，故 错误.故选 .
（2） 已知是定义在上的奇函数，对任意两个正数,，都有，且，则满足的的取值范围是 （ B ）
A. B.
C. D.
解：由题意，知 在 上单调递减.因为 是定义在
上的奇函数，所以 在 上单调递减，如图所示.
要使，则当 时，有，得；当 时，有，得.综上所述，满足 的 的取值范围是.故选.