2020春河南省新乡市中考数学模拟测试卷

这是一份2020春河南省新乡市中考数学模拟测试卷，共12页。试卷主要包含了﹣3的倒数的绝对值是，下列计算正确的是，一组数据2，不等式组的解集在数轴上可表示为等内容，欢迎下载使用。
选择题（12×3′＝36′）
1、﹣3的倒数的绝对值是（ ）
A.3 B.﹣3 C. D.
2、2018年参加我市中考的总人数约为人，用科学记数法应表示为（ ）
A、 B、 C、 D、
3、下列图形中，是中心对称图形但不是轴对称图形的是（ ）
4、下列计算正确的是（ ）
B.
C. D.
5、一组数据2、4、5、6、x的平均数是4，则这组数的标准差是（ ）
A、2 B、 C、10 D、
6、如图，△ABC中，AB=AC=4，BC=2，AB的垂直平分线
交AC于点D，交AB于点E，则△BCD的周长为（ ）
A、 B、 C、 D、
7、不等式组的解集在数轴上可表示为（ ）

8、如上右图，已知梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线交OB于D，且OD：DB＝1：2，若△OBC的面积等于3，则k的值是（ ）
A.等于2 B.等于 C.等于 D.无法确定
9、湖南电视台举行《我是歌手》大奖赛，每场比赛都有编号110号共10道综合素质试题供选手随机抽取作答。在某场比赛中，前两位选手分别抽走了2号，7号题（抽走的题不放回），则第三位选手抽走8号题的概率是（ ）
B. C. D.
10、某商场的老板销售一种商品，他要以不低于进价20%价格才能出售，但为了获得更多利润，他以高出进价80%的价格标价．若你想买下标价为360元的这种商品，最多降价多少时商店老板才能出售（ ）
A．80元 B．100元
C．120元 D．160元
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0，错误的个数有（ ）
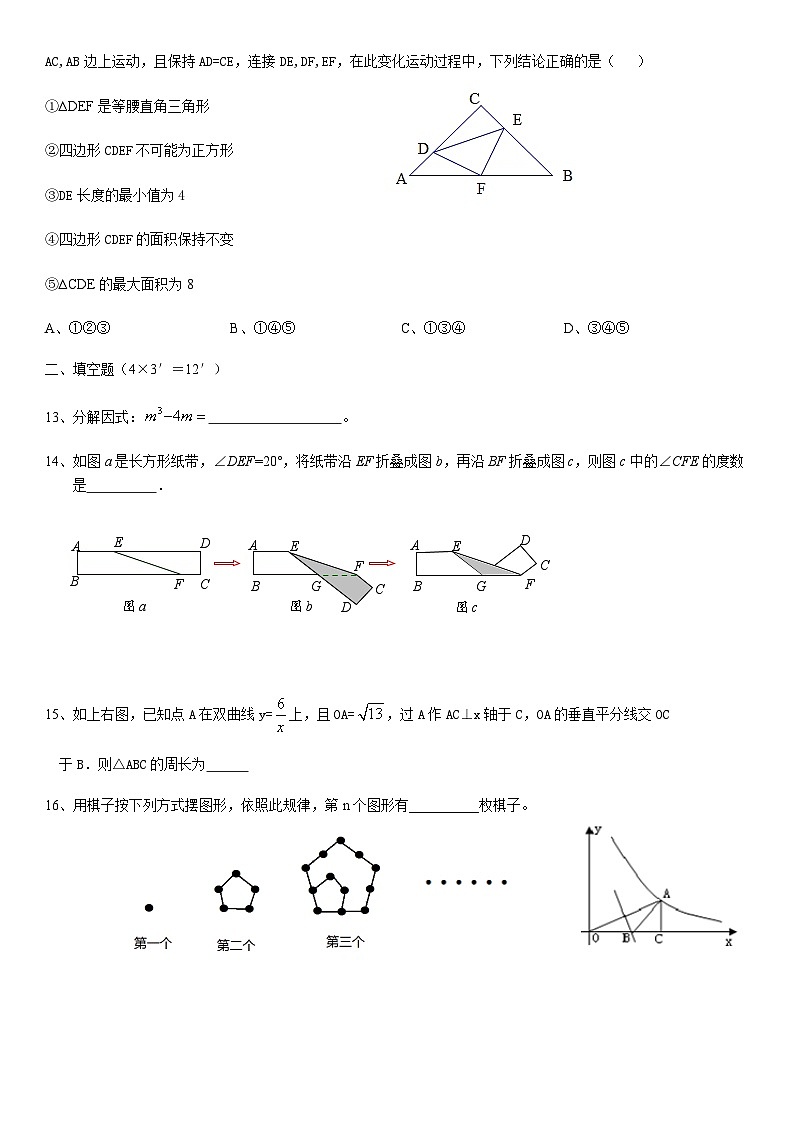
如图，在等腰Rt∆ABC中，∠C=90°，AC=8，F是AB边上的中点，点D,E分别在
AC,AB边上运动，且保持AD=CE，连接DE,DF,EF，在此变化运动过程中，下列结论正确的是（ ）
①∆DEF是等腰直角三角形
②四边形CDEF不可能为正方形
③DE长度的最小值为4
④四边形CDEF的面积保持不变
⑤∆CDE的最大面积为8
A、①②③ B、①④⑤ C、①③④ D、③④⑤
填空题（4×3′＝12′）
13、分解因式： 。
14、如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是 ．
A
DA
C
BA
EA
CA
BA
FA
DA
C
DBA
EA
FCA
GBA
A
BA
EA
FCA
GBA
A
图a
图b
图c
15、如上右图，已知点A在双曲线y=上，且OA=，过A作AC⊥x轴于C，OA的垂直平分线交OC
于B．则△ABC的周长为
16、用棋子按下列方式摆图形，依照此规律，第n个图形有__________枚棋子。
解答题（共52′）
17、（6′）．
（6′）先化简再求值： 其中x满足
19、（ 7分）“知识改变命运，科技繁荣祖国”．我区中小学每年都要举办一届科技比赛．下图为我区某校2019年参加科技比赛（包括电子百拼、航模、机器人、建模四个类别）的参赛人数统计图：
某校2015年科技比赛
参赛人数条形统计图
电子百拼
建模
机器人
航模
25%
25%
某校2015年航模比赛
参赛人数扇形统计图
参赛人数（单位：人）
参赛类别
0
2
电子百拼
6
8清8
4
航模
机器人
建模
6
6
4
（1）该校参加机器人、建模比赛的人数分别是 人和 人；（2分）
（2）该校参加科技比赛的总人数是 人，电子百拼所在扇形的圆心角的度数是 °，并把条形统计图补充完整；（3分）
（3）从全区中小学参加科技比赛选手中随机抽取80人，其中有32人获奖. 今年我区
中小学参加科技比赛人数共有2485人，请你估算今年参加科技比赛的获奖人数约是多少人?
20、（7分）如图，为⊙O的直径，，交于，，．
（1）求证：．（3分）（2）求AB长．（4分）
（8分）某商场将进价40元一个的某种商品按50元一个售出时，每月能卖出500个.商场想了两个方案来增加利润：方案一：提高价格，但这种商品每个售价涨价1元，销售量就减少10个；方案二：售价不变，但发资料做广告。已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p = ；试通过计算，请你判断商场为赚得更大的利润应选择哪种方案？请说明你判断的理由！
22、（9分）如图，在⊙O中，OA、OB是半径，且OA⊥OB，OA=6，点C是AB上异于A、B的动点。过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE（1）求证：四边形OGCH为平行四边形；（3分）（2）①当点C在AB上运动时，在CD、CG、DG中，是否存在长度不变的线段？若存在，请求出该线段的长度；若不存在，请说明理由；（3分）②求CD2+CH2之值。（3分）
O
B
E
C
H
G
D
A
（9分）已知如图，抛物线与轴交于A,B两点，与轴交于点C，∠ACB=90°，
求的值及抛物线的顶点坐标
过A、B、C三点的⊙M交轴于另一点D，连接DM并延长交⊙M于E，
过E点的⊙M的切线分别交轴，轴于F,G，求直线GF的解析式
（3）在条件（2）下，设P为上的一动点，（不与C，D重合），
连接PA交轴于H，问是否存在一个常数K，始终满足,
如果存在，请写出求解过程？若不存在，请说明理由。
参考答案
选择题
1、C 2、B 3、D 4、C 5、B 6、C 7、D 8、B 9、C 10、C 11、A 12、B
二、填空题
13、
14、120°
15、5
解答题
-8
（1）4，6；（2）24,120°；（3）994
（1）证明过程略；（2）AB=
21、设涨价x元，利润为y元，则
方案一：涨价x元时，该商品每一件利润为：50+x-40，销售量为：500-10x，
∴y=（50+x-40）（500-10x）=-10x2+400x+5000=-10（x-20）2+9000
∵当x=20时，y最大=9000，
∴方案一的最大利润为9000元；
方案二：该商品售价利润为=（50-40）×500p，广告费用为：1000m元，
∴y=（50-40）×500p-1000m=-2000m2+9000m=-2000（m-2.25）2+10125
∴方案二的最大利润为10125元；
∴选择方案二能获得更大的利润．
22、（1）证明：如右图，∵CD⊥OA，CE⊥OB，
∴∠ODC=∠OEC=90°
又∵∠AOB=90°，∴四边形OECD是矩形。
∴OD=EC，且OD//EC，∴∠ODG=∠CEH
∵DG=EH，∴△ODG≌△CEH，
∴OG=CH。
同理可证OH=CG
∴四边形OGCH为平行四边形
（2）①解：线段DG的长度不变。
∵点C是AB上的点，OA=6。∴OC=OA=6
∵四边形OECD是矩形，∴ED=OC=6
∵DG=GH=HE，∴DG=ED=2
②解：如右图，过点H作HF⊥CD于点F，
∵EC⊥CD，∴HF//EC
∴△DHF∽△DEC， ∴，∴
从而CF=CD-FD=CD
在Rt△CHF中，CH2=HF2+CF2=HF2+CD2
在Rt△HFD中，HF2=DH2-DF2=CD2
∴CH2=CD2+CD2=16-CD2
∴
23、解答：解：（1）由抛物线可知，点C的坐标为（0，m），且m＜0．
设A（，0），B（，0）．
则有=3m
又OC是Rt△ABC的斜边上的高，
∴△AOC∽△COB
∴
∴x1•x2=﹣m2
即﹣=3m，解得m=0或m=﹣3
而m＜0，
故只能取m=﹣3（3分）
这时y=﹣4
故抛物线的顶点坐标为（，﹣4）．
（2）由已知可得：M（，0），A（﹣，0），B（3，0），
C（0，﹣3），D（0，3）
∵抛物线的对称轴是x=，也是⊙M的对称轴，连接CE
∵DE是⊙M的直径，
∴∠DCE=90°，
∴直线x=，垂直平分CE，
∴E点的坐标为（2，﹣3）
∵，∠AOC=∠DOM=90°，
∴∠ACO=∠MDO=30°，
∴AC∥DE
∵AC⊥CB，
∴CB⊥DE
又∵FG⊥DE，
∴FG∥CB
由B（3，0）、C（0，﹣3）两点的坐标易求直线CB的解析式为：
y=﹣3
可设直线FG的解析式为y=+n，把（2，﹣3）代入求得n=﹣5
故直线FG的解析式为y=﹣5．
（3）存在常数k=12，满足AH•AP=12，
假设存在常数k，满足AH•AP=k
连接CP，
∵AB⊥CD，
∴=
∴∠P=∠ACH（或利用∠P=∠ABC=∠ACO），
又∵∠CAH=∠PAC，
∴△ACH∽△APC，
=，
∴即=AH•AP，
在Rt△AOC中，AC2=AO2+OC2=（）2+（3）2 =12，
∴AH•AP=k=12；

A．
1个
B．
2个
C．
3个
D．
4个