2024年云南省昆明市中考二模数学试题(无答案)

这是一份2024年云南省昆明市中考二模数学试题(无答案)，共6页。试卷主要包含了本卷为试题卷，下列计算正确的是等内容，欢迎下载使用。
（全卷三个大题，共27个小题，共6页；满分100分，考试用时120分钟）
注意事项：
1.本卷为试题卷。考生必须在答题卡上解题作答。答案应书写在答题卡的相应位置上，在试题卷、草稿纸上作答无效。
2.考试结束后，将答题卡交回，试题卷自己收好，以便讲评。
一、选择题（本大题共15小题，每小题只有一个正确选项，每小题2分，共30分）
1.九年级（1）班期末考试数学的平均成绩是80分，小亮得了90分，记作+10分，如果小明的成绩记作分，那么他得了（ ）
A.95分B.90分C.85分D.75分
2.苏步青是中国著名的数学家，被誉为“数学之王”，为纪念其贡献，国际上将一颗距地球约218000000千米的小行星命名为“苏步青星”，将218000000用科学记数法表示为的形式（其中，n是正整数），则n的值为（ ）
A.6B.7C.8D.9
3.用高和底面圆的直径相等的4个圆柱体组成如图所示的立体图形，它的俯视图是（ ）
A.B.C.D.
4.下列计算正确的是（ ）
A.B.
C.D.
5.能使下列某个式子有意义，这个式子是（ ）
A.B.C.D.
6.数学活动课上，李老师给出一组按一定规律排列的数：2，，8，，32，…，第n个数是（ ）
A.B.C.D.
7.卷云纹是我国独特的传统装饰纹样，古代玉璧上的卷云纹纹饰优雅，寓意美好，下列四个选项中，是轴对称图形但不是中心对称图形的是（ ）
A.B.C.D.
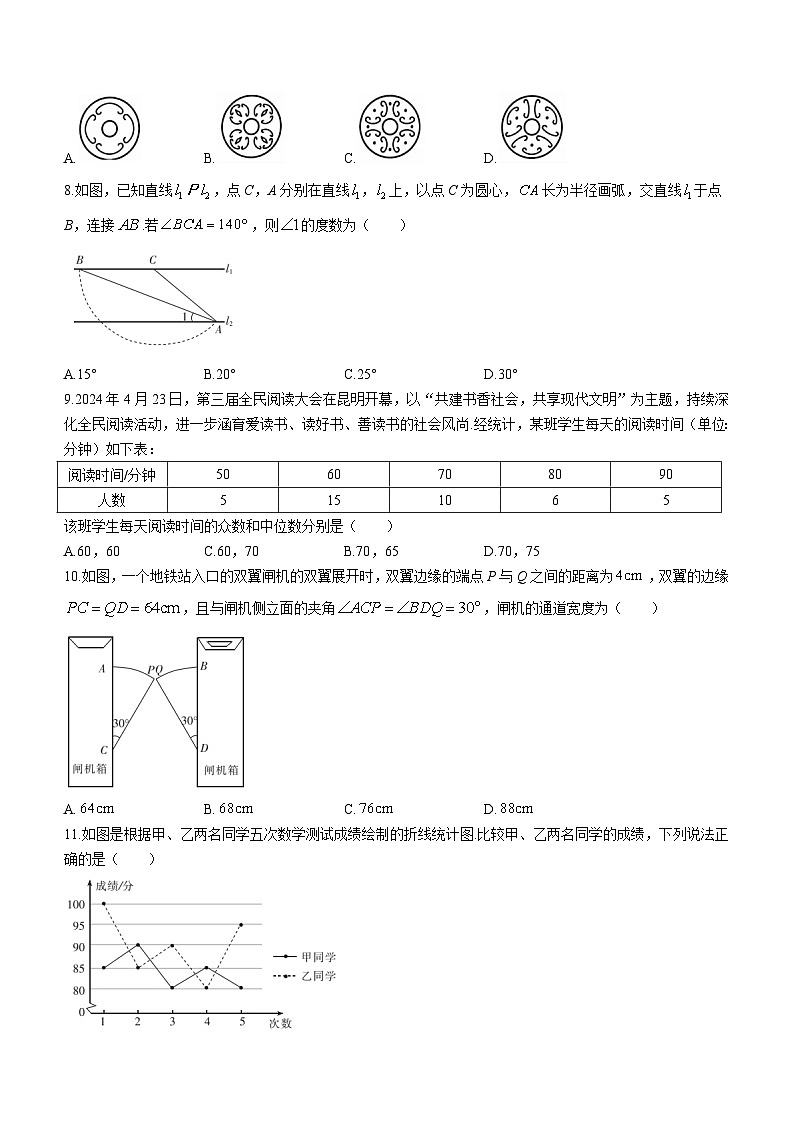
8.如图，已知直线，点C，A分别在直线，上，以点C为圆心，长为半径画弧，交直线于点B，连接.若，则的度数为（ ）
A.15°B.20°C.25°D.30°
9.2024年4月23日，第三届全民阅读大会在昆明开幕，以“共建书香社会，共享现代文明”为主题，持续深化全民阅读活动，进一步涵育爱读书、读好书、善读书的社会风尚.经统计，某班学生每天的阅读时间（单位：分钟）如下表：
该班学生每天阅读时间的众数和中位数分别是（ ）
A.60，60C.60，70B.70，65D.70，75
10.如图，一个地铁站入口的双翼闸机的双翼展开时，双翼边缘的端点P与Q之间的距离为，双翼的边缘，且与闸机侧立面的夹角，闸机的通道宽度为（ ）
A.B.C.D.
11.如图是根据甲、乙两名同学五次数学测试成绩绘制的折线统计图.比较甲、乙两名同学的成绩，下列说法正确的是（ ）
A.甲同学成绩的平均分高，方差大
B.甲同学成绩的平均分高，方差小
C.乙同学成绩的平均分高，方差大
D.乙同学成绩的平均分高，方差小
12.如图，是的外接圆，是的直径.若，则的度数是（ ）
A.36°B.33°C.30°D.27°
13.已知，估计c的值所在的范围是（ ）
A.B.C.D.
14.如图，，是的两条中线，连接.若，则阴影部分的面积是（ ）
A.2B.4C.6D.8
15.如图，一个棱长为15的正方体木块，从它的八个顶点处依次截去棱长分别为1，2，3，4，5，6，7，8的小正方体，最后得到的几何体的表面积是（ ）
A.
B.
C.或
D.或
二、填空题（本大题共4小题，每小题2分，共8分）
16.分解因式：______
17.如图，一个正n边形被树叶遮掩了一部分，若直线a，b所夹锐角为36°，则n的值是______.
18.下表是几组y与x的对应值，则y关于x的函数解析式为______.
19.如图，吊灯外罩呈圆锥形，它的底面周长为，高为，则该吊灯外罩的侧面积是______.（结果保留）
三、解答题（本大题共8小题，共62分）
20.（本小题满分7分）
计算：.
21.（本小题满分6分）
如图，，，.
求证：.
22.（本小题满分6分）
某校开设智能机器人编程的活动课，购买了A，B两种型号的机器人模型.A型机器人模型单价比B型机器人模型单价多200元，用2800元购买A型机器人模型和用2000元购买B型机器人模型的数量相同.A型、B型机器人模型的单价分别是多少元？
23.（本小题满分7分）每年4月至5月，昆明的蓝花楹陆续盛开.一条条平日里不起眼的街道在披上了蓝紫色的轻纱后摇身一变，成了大家纷纷前往打卡的“网红”路.游客小迅从住宿的A地出发，要先经B地再到“网红”路C地游览.如图，从A地到B地共有三条路线，长度分别为，，，从B地到C地共有两条路线，长度分别为，.
（1）小迅从A地到B地所走路线长为的概率为______；
（2）请用列表法或画树状图法中的一种方法，求小迅从A地经B地再到C地所走路线总长度为的概率.
24.（本小题满分8分）
为调动实习员工工作的积极性，某公司出台了两种工资方案，实习员工任选其中一种方案与公司签订合同.方案一：月工资y（单位：元）与生产的产品数量x（单位：件）的函数关系如图所示；方案二：每生产一件产品可得25元.
（1）选择了工资方案一的实习员工甲，第一个月生产了60件产品，他该月得到的工资是多少元？
（2）某月实习员工乙发现，他选择方案一比选择方案二月工资多450元，求乙该月生产工产品的数量.
25.（本小题满分8分）
如图，在菱形中，对角线，交于点O，过点A作于点E，延长到点F，使得，连接.
（1）求证：四边形是矩形；
（2）连接，若，，求的长.
26.（本小题满分8分）
如图，内接于，过点C作射线，使得，与的延长线交于点P，D是的中点，与交于点E.
（1）判断直线与的位置关系，并证明你的结论；
（2）若，求证：.
27.（本小题满分12分）
如果一个点的横、纵坐标均为常数，那么我们把这样的点称为确定的点，简称定点.比如点就是一个定点.对于一次函数（k是常数，），由于，当即时，无论k为何值，y一定等于3，我们就说直线一定经过定点.设抛物线（m是常数，）经过的定点为点D，顶点为点P.
（1）抛物线经过的定点D的坐标是______；
（2）是否存在实数m，使顶点P在x轴上？若存在，求出m的值；若不存在，请说明理由；
（3）当时，在的图象上存在点Q，使得这个点到点P、点D的距离的和最短.求k的取值范围.
阅读时间/分钟
50
60
70
80
90
人数
5
15
10
6
5
x
…
1
2
3
…
y
…
3
4.5
9
…