2024年安徽省合肥市肥西县中考数学二模试卷（含解析）

这是一份2024年安徽省合肥市肥西县中考数学二模试卷（含解析），共21页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.下列各数中，比−2小的数是( )
A. 0B. −3C. −1D. 4
2.如图，该三棱柱的主视图是( )
A.
B.
C.
D.
3.我国南海海域的面积约为3 600 000km2，该面积用科学记数法应表示为( )
A. 36×105km2B. 3.6×105km2C. 3.6×106km2D. 0.36×107km2
4.下列运算正确的是( )
A. 4m2·2m3=8m6B. (−m2)3=−m6
C. −m(−m+2)=−m2−2mD. m2+m3=m6
5.关于x的一元二次方程2x2−3x+32=0根的情况，下列说法中正确的是( )
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 没有实数根D. 无法确定
6.在数−1，1，2中任取两个数作为点坐标，那么该点刚好在一次函数y=x−2图象上的概率是( )
A. 12B. 13C. 14D. 16
7.半径为R的圆内接正三角形、正方形、正六边形的边心距分别为a，b，c，则a，b，c的大小关系是( )
A. a8.如图，在给定的一张平行四边形纸片上作一个菱形．甲、乙两人的作法如下：
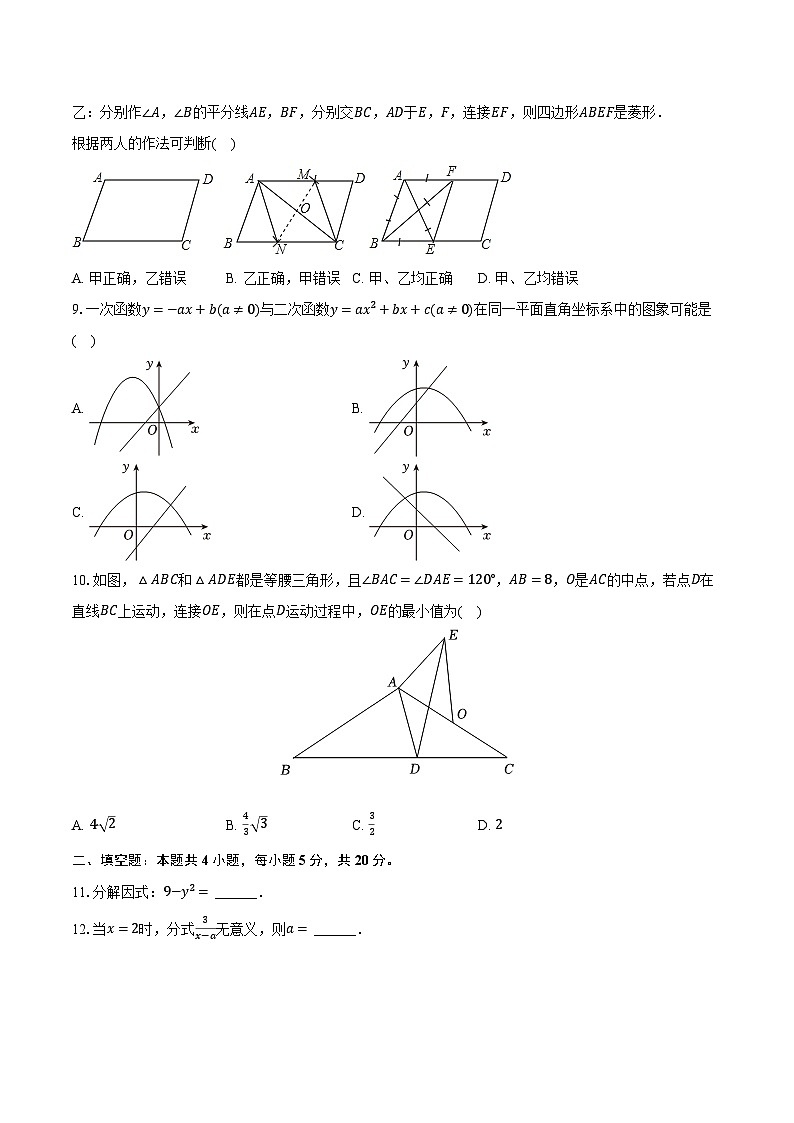
甲：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．
乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形．
根据两人的作法可判断( )
A. 甲正确，乙错误B. 乙正确，甲错误C. 甲、乙均正确D. 甲、乙均错误
9.一次函数y=−ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
10.如图，△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE=120°，AB=8，O是AC的中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，OE的最小值为( )
A. 4 2B. 43 3C. 32D. 2
二、填空题：本题共4小题，每小题5分，共20分。
11.分解因式：9−y2= ______．
12.当x=2时，分式3x−a无意义，则a= ______．
13.如图，在矩形ABCD中，AB=9，AD=15，点E是CD边上的一点，连接AE，将△ADE沿AE翻折，使点D恰好落在BC边上的点F处，则S△ECFS△FBA= ______．
14.如图，在Rt△ABC中，∠ABC=90°，C(0,−4)，AC与x轴交于点D．
(1)若OB=1，求tan∠OBC= ______．
(2)若CD=4AD，点A在y=kx(x>0)的图象上，且y轴平分∠ACB，求k= ______．
三、计算题：本大题共1小题，共8分。
15.计算：|− 3|−(3−π)0+tan45°+(12)−1．
四、解答题：本题共8小题，共82分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
几个人共种一批树苗，如果每人种10棵，则剩下6棵树苗未种；如果每人种12棵，则缺6棵树苗．求参与种树的人数是多少？
17.(本小题8分)
有下列等式：
第1个等式：34=1−14；
第2个等式：37=12−114；
第3个等式：310=13−130；
第4个等式：313=14−152；
…
请你按照上面的规律解答下列问题：
(1)第5个等式是______；
(2)写出你猜想的第n个等式：______(用含n的等式表示)，并证明其正确性．
18.(本小题8分)
如图，在边长为1的小正方形组成的网格中，给出了格点△ABC(顶点为网格线的交点)．
(1)将△ABC先向下平移3个单位长度，再向右平移4个单位长度得到△A1B1C1，画出平移后的图形．
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2，画出旋转后的图形；
(3)借助网格，利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法)．
19.(本小题10分)
如图，游客从旅游景区山脚下的地面A处出发，沿坡角α=30°的斜坡AB步行50m至山坡B处，乘直立电梯上升30m至C处，再乘缆车沿长为180m的索道CD至山顶D处，此时观测C处的俯角为19°30′，索道CD看作在一条直线上.求山顶D的高度.(精确到1m，sin19°30′≈0.33，cs19°30′≈0.94，tan19°30′≈0.35)
20.(本小题10分)
如图，AB是⊙O的直径，C是⊙O上一点，D是AC的中点，E为OD延长线上一点，且∠CAE=2∠C，AC与BD交于点H，与OE交于点F．
(1)求证：AE是⊙O的切线；
(2)若DH=9，tanC=34，求直径AB的长．
21.(本小题12分)
每年5月份是心理健康宣传月，某中学开展以“关心他人，关爱自己”为主题的心理健康系列活动．为了解师生的心理健康状况，对全体2000名师生进行了心理测评，随机抽取20名师生的测评分数进行了以下数据的整理与分析：
①数据收集：抽取的20名师生测评分数如下
85，82，94，72，78，89，96，98，84，65，
73，54，83，76，70，85，83，63，92，90．
②数据整理：将收集的数据进行分组并评价等级：
③数据分析：绘制成不完整的扇形统计图：
④依据统计信息回答问题
(1)统计表中的a=______．
(2)心理测评等级C等的师生人数所占扇形的圆心角度数为______．
(3)学校决定对E等的师生进行团队心理辅导，请你根据数据分析结果，估计有多少师生需要参加团队心理辅导？
22.(本小题12分)
如图，在正方形ABCD中，点M是边BC上的一点(不与B、C重合)，点N在边CD延长线上，且满足∠MAN=90°，联结MN，AC，MN与边AD交于点E．
(1)求证：AM=AN；
(2)如果∠CAD=2∠NAD，求证：AM2= 2AB⋅AE；
(3)MN交AC点O，若CMBM=k，则OMON=______(直接写答案、用含k的代数式表示)．
23.(本小题14分)
如图1，一灌溉车正为绿化带浇水，喷水口H离地竖直高度为h=1.2米.建立如图2所示的平面直角坐标系，可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象，把绿化带横截面抽象为矩形DEFG，其水平宽度DE=2米，竖直高度EF=0.7米，下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2米，高出喷水口0.4米，灌溉车到绿化带的距离OD为d米．
(1)求上边缘抛物线喷出水的最大射程OC；
(2)求下边缘抛物线与x轴交点B的坐标；
(3)若d=3.2米，通过计算说明灌溉车行驶时喷出的水能否浇灌到整个绿化带．
答案和解析
1.【答案】B
【解析】解：∵−3<−2<−1<0<4，
∴比−2小的数是−3，
故选：B．
根据有理数的大小比较法则：正数大于0，负数小于0，正数总大于负数，负数绝对值大的反而小即可得答案．
本题考查了有理数的大小比较法则，熟记比较法则是解题关键．
2.【答案】A
【解析】解：从正面看，是一个矩形，矩形内部有一条纵向的虚线．
故选：A．
主视图是从正面看所得到的图形即可，可根据直三棱柱的特点作答．
本题考查简单几何体的三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．
3.【答案】C
【解析】解：将3 600000用科学记数法表示为3.6×106．
故选C．
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．
本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
4.【答案】B
【解析】解：A、4m2·2m3=8m5，故此选项错误；
B、(−m2)3=−m6，故此选项正确；
C、−m(−m+2)=m2−2m，故此选项错误；
D、m2+m3，不是同类项无法合并，故此选项错误；
故选：B．
直接利用单项式乘以多项式和积的乘方运算法则、合并同类项法则分别计算得出答案．
此题主要考查了单项式乘以多项式和积的乘方运算、合并同类项，正确掌握相关运算法则是解题关键．
5.【答案】C
【解析】解：∵a=2，b=−3，c=32，
∴b2−4ac=9−12=−3<0，
∴方程没有实数根．
故选：C．
先确定a、b、c的值，在计算b2−4ac即可．
此题考查了根的判别式，一元二次方程中根的判别式大于0，方程有两个不相等的实数根；根的判别式等于0，方程有两个相等的实数根；根的判别式小于0，方程无解．
6.【答案】D
【解析】解：画树状图如下：
共有6种等可能的结果，其中只有(1,−1)在一次函数y=x−2图象上，
所以点在一次函数y=x−2图象上的概率=16．
故选D．
先画树状图展示所有6种等可能的结果，而只有(1,−1)在一次函数y=x−2图象上，然后根据概率的概念即可计算出点刚好在一次函数y=x−2图象上的概率．
本题考查了利用列表法或树状图法求概率：先列表或画树状图展示所有等可能的结果，再找出某事件所占有的可能数，然后根据概率的概念求这个事件的概率．也考查了点在一次函数图形上，则点的横纵坐标满足一次函数的解析式．
7.【答案】A
【解析】【分析】
此题主要考查了正多边形和圆的性质，解决本题的关键是构造直角三角形，得到用半径表示的边心距；注意：正多边形的计算一般要转化为解直角三角形的问题来解决．
根据三角函数即可求解．
【解答】
解：设圆的半径为R，
则正三角形的边心距为a=R×cs60°=12R.
正方形的边心距为b=R×cs45°= 22R，
正六边形的边心距为c=R×cs30°= 32R.
∵12R< 22R< 32R，
∴a故选：A．
8.【答案】C
【解析】【分析】
此题主要考查了菱形的判定，关键是掌握菱形的判定方法．
甲：首先证明△AOM≌△CON(ASA)，可得MO=NO，再根据对角线互相平分的四边形是平行四边形可判定判定四边形ANCM是平行四边形，再由AC⊥MN，可根据对角线互相垂直的平行四边形是菱形判定出ANCM是菱形．乙：四边形ABCD是平行四边形，可根据角平分线的定义和平行线的定义，求得AB=AF，所以四边形ABEF是菱形．
【解答】
解：甲的作法正确；
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠DAC=∠ACN，
∵MN是AC的垂直平分线，
∴AO=CO，
在△AOM和△CON中
∠MAO=∠NCOAO=CO∠AOM=∠CON，
∴△AOM≌△CON(ASA)，
∴MO=NO，
∴四边形ANCM是平行四边形，
∵AC⊥MN，
∴四边形ANCM是菱形；
乙的作法正确；
∵AD/​/BC，
∴∠1=∠2，∠6=∠7，
∵BF平分∠ABC，AE平分∠BAD，
∴∠2=∠3，∠5=∠6，
∴∠1=∠3，∠5=∠7，
∴AB=AF，AB=BE，
∴AF=BE
∵AF/​/BE，且AF=BE，
∴四边形ABEF是平行四边形，
∵AB=AF，
∴平行四边形ABEF是菱形；
故选：C．
9.【答案】B
【解析】解：A选项，根据一次函数的位置可知，a<0，b>0，
∴抛物线开口向下，−ba>0，抛物线的对称轴−b2a>0，A选项不符合题意；
B选项，根据一次函数的位置可知，a<0，b>0，
∴抛物线开口向下，−ba>0，抛物线的对称轴−b2a>0，B选项符合题意；
C选项，根据一次函数的位置可知，a<0，b<0，
∴抛物线开口向下，−ba<0，抛物线的对称轴−b2a<0，C选项不符合题意；
D选项，根据一次函数的位置可知，a>0，b>0，抛物线开口向上，D选项不符合题意；
故选：B．
利用一次函数的图象位置与系数的关系，二次函数的图象位置与系数的关系判断．
本题考查了二次函数的图象与一次函数的图象，解题的关键是掌握一次函数的图象位置与系数的关系，二次函数的图象位置与系数的关系．
10.【答案】D
【解析】解：设AB的中点为Q，连接DQ，过点Q作QH⊥|BC于H，如下图所示：
∵△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE=120°，
∴AB=AC，AD=AE，∠QAD+∠DAC=∠DAC+∠OAE=120°，
∴∠QAD=∠OAE，
∵点Q是AB的中点，点O是AC的中点，AB=AC，
∴AQ=AO，
在△AQD和△AOE中，
AQ=AO∠QAD=∠OAEAD=AE，
∴△AQD≌△AOE(SAS)，
∴QD=OE，
∴当QD为最小时，OE为最小，
∵点Q为AB的中点，AB=8，点D在直线BC上运动，
∴根据“垂线段最短”得：QD≥QH，
∴当点D与点H重合时，QD为最小，最小值为QH的长，
在△ABC中，AB=AC=8，∠BAC=120°，
∴∠B=∠C=12(180°−∠BAC)=30°，
在Rt△BQH中，∠B=30°，BQ=12AB=4，
∴QH=12BQ=2，
∴QD的最小值为2，
即OE的最小值为2．
故选：D．
设AB的中点为Q，连接DQ，过点Q作QH⊥|BC于H，证△AQD和△AOE全等得QD=OE，因此当QD为最小时，OE为最小，根据“垂线段最短”得QD≥QH，故点D与点H重合时，QD为最小，最小值为QH的长，然后在Rt△BQH中求出QH的长即可．
此题主要考查了等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，垂线段的性质，熟练掌握等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，理解垂线段最短是解决问题的关键，难点是正确地作出辅助线构造全等三角形和直角三角形．
11.【答案】(3+y)(3−y)
【解析】解：9−y2=(3+y)(3−y)．
故答案为：(3+y)(3−y)．
直接利用平方差公式分解因式即可．
此题主要考查了因式分解−运用公式法，正确应用平方差公式是解题关键．
12.【答案】2
【解析】解：∵当x=2时，分式3x−a无意义，
∴a=2．
故答案为：2．
根据分式有意义的条件得出答案即可．
本题考查了分式有意义的条件，能熟记当分母B=0时分式AB(A、B为整式)无意义是解此题的关键．
13.【答案】19
【解析】解：在矩形ABCD中，根据折叠的性质，可得AD=AF=15，DE=EF，∠AFE=ADE=90°，BF= AF2−AB2= 152−92=12；
∵∠AFE=90°，
∴∠AFB+∠EFC=90°，
∵∠AFB+∠FAB=90°，
∴∠EFC=∠FAB，
∵∠ABF=∠FCE=90°，
∴△FBA∽△ECF，
∴EFEC=AFBF=1512=54；
设DE=EF=x，则EC=9−x，
∵EFEC=54，
∴x9−x=54，解得：x=5，
∴EFAF=515=13；
∵△ECF∽△FBA，
∴S△ECFS△FBA=(EFAF)2=(13)2=19．
故答案为：19．
根据折叠的性质，可得AD=AF=15，DE=EF，BF= AF2−AB2=12；∠AFE=ADE=90°，∠ABF=∠AFE=∠FCE=90°，△ABF∽△FCE，EFEC=AFBF=1512=54；设DE=EF=x，则EC=9−x，EFEC=x9−x=54，解得：x=5，则EFAF=515=13；△ECF∽△FBA，S△ECFS△FBA=(EFAF)2=(13)2=19．
本题考查了形似三角形的性质，熟练掌握矩形、折叠变换、相似三角形的性质是解本题的关键，综合性较强，难度适中．
14.【答案】4 53
【解析】解：(1)∵C(0,−4)，
∴OC=4，
在Rt△BOC中，OB=1，OC=4，
tan∠OBC=OCOB=4．
故答案为：4．
(2)如图，作AE⊥x轴，垂足为E，
∵∠AED=∠COD=90°，∠ADE=∠CDO，
∴△ADE∽△CDO，
∵CD=4AD，
∴AECO=DEOD=ADCD=14，
∴AE=1，
又∵y轴平方∠ACB，CO⊥BD，
∴BO=OD，
∵∠ABC=90°，
∴∠OCD=∠DAE=∠ABE，
∴△ABE∽△DCO，
∴AEOD=BEOC，
设DE=n.则BO=OD=4n，BE=9n，
∴14n=9n4，
∴n=13，
∴OE=5n=53，
∴A(53,1)，
∴k=53．
故答案为：53．
(1)根据正切的定义代入数据计算即可；
(2)作AE⊥x轴，利用条件证明△ADE∽△CDO得到AE=1，再利用条件证明△ABE∽△DCO列出AEOD=BEOC，设DE=n.则BO=OD=4n，BE=9n，根据相似比代入计算出n值，得到A(53,1)，根据反比例函数图象上点的坐标特征求出k值即可．
本题考查了反比例函数图象上点的坐标特征，熟练掌握相似三角形性质是解答本题的关键．
15.【答案】解：|− 3|−(3−π)0+tan45°+(12)−1
= 3−1+1+2
= 3+2．
【解析】此题主要考查了实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．
首先计算绝对值，零指数幂，特殊角的三角函数值，负整数指数幂，然后从左向右依次计算，求出算式的值即可．
16.【答案】解：设参与种树的人数是x人，
依题意得：10x+6=12x−6，
解得：x=6．
答：参与种树的人数是6人．
【解析】设参与种树的人数是x人，根据“如果每人种10棵，则剩下6棵树苗未种；如果每人种12棵，则缺6棵树苗”，即可得出关于x的一元一次方程，解之即可求出参与种树的人数．
本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
17.【答案】解：(1)316=15−180
(2)根据题意得，第n个等式为：33n+1=1n−1n(3n+1)．
证明：右边=3n+1−1n(3n+1)=3nn(3n+1)=33n+1=左边，
∴33n+1=1n−1n(3n+1)．
故答案为：33n+1=1n−1n(3n+1)．
【解析】解：(1)第1个等式：34=1−14，即33×1+1=11−11×4；
第2个等式：37=12−114，即33×2+1=12−12×(3×2+1)；
第3个等式：310=13−130，即33×3+1=13−13×(3×3+1)；
第4个等式：313=14−152，即33×4+1=14−14×(3×4+1)；
…
由上规律可知，第5个等式是33×5+1=15−15×(3×5+1)，即316=15−180，
故答案为：316=15−180；
(1)观察算式得出规律：分子为3，分母比序号数的3倍大1，这样的分数等于序号数的倒数减去序号数与比序号数的3倍大1的数的积的倒数．按此规律写出第5个等式便可；
(2)用n表示上面的规律，并运用分式的减法运算进行验证．
此题考查数字的变化规律，通过观察，分析、归纳找到规律，并能利用规律计算，并能证明结论是正确．
18.【答案】解：(1)如图，△A1B1C1即为所求．
(2)如图，△A2B2C2即为所求．
(3)如图，线段A1D1即为所求．

【解析】(1)分别作出A，B，C的对应点A1，B1，C1即可．
(2)分别作出A，B，C的对应点A2，B2，C2即可．
(3)取格点K，连接A1K交B1C1于D，线段AD即为所求．
本题考查作图−旋转变换，平移变换等知识，解题的关键是熟练掌握基本知识属于中考常考题型．
19.【答案】解：如图，过点C、B分别作CE⊥DG，BF⊥DG垂足为E、F，延长CB交AG于点H，
由题意可知，∠DCE=19°30′，CD=180m，BC=EF=30m，
在Rt△ABH中，∠α=30°，AB=50m，
∴BH=12AB=25m，
∴FG=25m
在Rt△DCE中，∠DCE=19°30′，CD=180m，
∴DE=sin∠DCE⋅CD≈0.33×180=59.4m，
∴DG=DE+EF+FG=59.4+30+25=114.4≈114m，
答：山顶D的高度约为114m．
【解析】通过作垂线，构造直角三角形，利用直角三角形的边角关系分别求出DE，FG即可．
本题考查解直角三角形，掌握直角三角形的边角关系是正确解答的前提，构造直角三角形是解决问题的关键..
20.【答案】解：(1)∵D是AC的中点，
∴OE⊥AC，
∴∠AFE=90°，
∴∠E+∠EAF=90°，
∵∠AOE=2∠C，∠CAE=2∠C，
∴∠CAE=∠AOE，
∴∠E+∠AOE=90°，
∴∠EAO=90°，
∴AE是⊙O的切线；
(2)连接AD，在Rt△ADH中，
∵∠DAC=∠C，
∴tan∠DAC=tanC=34，
∵DH=9，
∴AD=12，
在Rt△BDA中，∵tanB=tanC=34，
∴sinB=35，
∴AB=20．
【解析】本题考查了切线的判定，圆周角定理，垂径定理，和锐角三角函数解直角三角形，正确的识别图形是解题的关键．
(1)根据垂径定理得到OE⊥AC，求得∠AFE=90°，求得∠EAO=90°，于是得到结论；
(2)根据等腰三角形的性质和垂径定理得到∠DAC=∠C，求得tan∠DAC=tanC=34，由DH的长可求得AD，由圆周角定理得tanB=tanC=34，可得sinB=35，即可求得AB．
21.【答案】解：(1)7；
(2)90°；
(3)2000×120=100(人)，
答：估计有100名师生需要参加团队心理辅导．
【解析】解：
(1)总人数=2÷10%=20(人)，a=20×35%=7，故答案为7．
(2)C所占的圆心角=360°×520=90°，故答案为90°．
(3)见答案
(1)根据D组人数以及百分比求出总人数，再求出a即可．
(2)根据圆心角=360°×百分比计算即可．
(3)利用样本估计总体的思想解决问题即可．
本题考查扇形统计图，样本估计总体的思想，频数分布表等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
22.【答案】kk+2
【解析】证明(1)∵四边形ABCD是正方形，
∴AB=AD，∠CAD=∠ACB=45°，∠BAD=∠CDA=∠B=90°，
∴∠BAM+∠MAD=90°，
∵∠MAN=90°，
∴∠MAD+∠DAN=90°，
∴∠BAM=∠DAN，
∵AD=AB，∠ABC=∠ADN=90°，
∴△ABM≌△ADN(ASA)，
∴AM=AN．
(2)∵AM=AN，∠MAN=90°，
∴∠MNA=45°，
∵∠CAD=2∠NAD=45°，
∴∠NAD=22.5°
∴∠CAM=∠MAN−∠CAD−∠NAD=22.5°
∴∠CAM=∠NAD，∠ACB=∠MNA=45°，
∴△AMC∽△AEN，
∴AMAE=ACAN，
∴AM⋅AN=AC⋅AE，
∵AN=AM，AC= 2AB，
∴AM2= 2AB⋅AE；
(3)OMON=kk+2．
理由：如图，过点M作MF/​/AB交AC于点F，
设BM=a，
∵CMBM=k，
∴BM=a，BC=(k+1)a，
即ND=BM=a，AB=CD=BC=(k+1)a，
∵MF//AB//CD，
∴MFAB=CMCB=k1+k，
∴MF=ka，
∴OMON=MFCN=ka(k+1+1)a=kk+2．
故答案为：kk+2．
(1)由正方形的性质可得AB=AD，由“ASA”可证△ABM≌△ADN，可得AM=AN；
(2)由题意可得∠CAM=∠NAD=22.5°，∠ACB=∠MNA=45°，即可证△AMC∽△AEN，即可证AM2=AE⋅AC，再根据AC= 2AB可得结论；
(3)过点M作MF/​/AB交AC于点F，设BM=a，由CMBM=k，BM=a，BC=(k+1)a，再根据OMON=MFCN可得答案．
此题是相似形综合题，主要考查了正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，判断出△BAM∽△FAO是解本题的关键．
23.【答案】解：(1)如图2，由题意得A(2,1.6)是上边缘抛物线的顶点，
设y=a(x−2)2+1.6，
又∵抛物线过点(0,1.2)，
∴1.2=4a+1.6，
∴a=−110，
∴上边缘抛物线的函数解析式为y=−110(x−2)2+1.6，
当y=0时，0=−110(x−2)2+1.6，
解得x1=6，x2=−2(舍去)，
∴喷出水的最大射程OC为6m；
(2)∵对称轴为直线x=2，
∴点(0,1.2)的对称点为(4,1.2)，
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的，
∴点B的坐标为(2,0)；
(3)∵OD=d=3.2米，DE=2米，EF=0.7米，
∴点F的坐标为(5.2,0.7)，
当x=5.2时，y=−110(5.2−2)2+1.6=72125=0.576<0.7，
当x>2时，y随x的增大而减小，
∴灌溉车行驶时喷出的水不能浇灌到整个绿化带．
【解析】(1)由顶点A(2,1.6)得，设y=a(x−2)2+1.6，再根据抛物线过点(0,1.2)，可得a的值，从而解决问题；
(2)由对称轴知点(0,1.2)的对称点为(4,1.2)，则下边缘抛物线是由上边缘抛物线向左平移4cm得到的，可得点B的坐标；
(3)根据OD=d=3.2米，DE=2米，EF=0.7米，可求得点F的坐标为(5.2,0.7)，当x=5.2时，y=−110(5.2−2)2+1.6=72125=0.576<0.7，从而得出答案．
本题考查二次函数的实际应用，掌握待定系数法求二次函数解析式，二次函数的性质，二次函数与方程的关系等知识，读懂题意，建立二次函数模型是解题的关键．分数x
90≤x<100
80≤x<90
70≤x<80
60≤x<70
x<60
人数
5
a
5
2
1
等级
A
B
C
D
E