

2023-2024学年江苏省无锡市辅仁高级中学高一(下)期中数学试卷(含解析)
展开1.已知平面向量a=(−1,4),b=(x,2),且a⊥b,则x=( )
A. −8B. −12C. 12D. 8
2.设l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
A. 若m//n,n//α,则m//α
B. 若α//β,l//α,则l//β
C. 若α//β,l⊂α,则l//β
D. 若m//β,n//β,m⊂α,n⊂α,则α//β
3.在△ABC中,角A,B,C的对边分别为a,b,c,若a=2,B=π3,△ABC的面积等于2 3,则b的大小为( )
A. 2 3B. 13C. 4D. 21
4.古希腊数学家特埃特图斯(Theaetetus)利用如图所示的直角三角形来构造无理数.已知AB=BC=CD=2,AB⊥BC,AC⊥CD,若DB=λAB+μAC,则λ+μ=( )
A. − 22
B. 22
C. 2+12
D. 2−12
5.如图,实心正方体ABCD−A1B1C1D1的棱长为2,其中上、下底面的中心分别为Q,R.若从该正方体中挖去两个圆锥,且其中一个圆锥以R为顶点,以正方形A1B1C1D1的内切圆为底面,另一个圆锥以Q为顶点,以正方形ABCD的内切圆为底面,则该正方体剩余部分的体积为( )
A. 8−5π12B. 8−7π12C. 8−5π6D. 8−7π6
6.已知e是单位向量,且|2e−a|= 10,a+2e在e上的投影向量为5e,则a与e的夹角为( )
A. π6B. π4C. π3D. 5π12
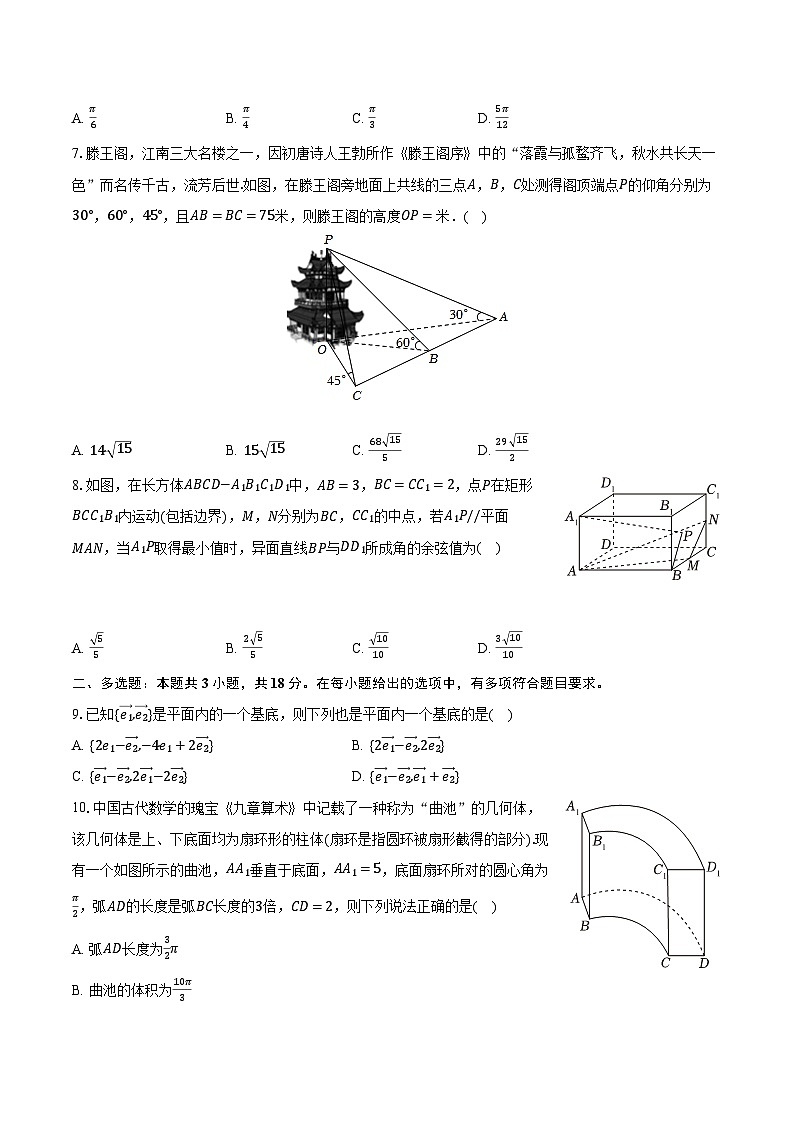
7.滕王阁,江南三大名楼之一,因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞,秋水共长天一色”而名传千古,流芳后世.如图,在滕王阁旁地面上共线的三点A,B,C处测得阁顶端点P的仰角分别为30°,60°,45°,且AB=BC=75米,则滕王阁的高度OP=米.( )
A. 14 15B. 15 15C. 68 155D. 29 152
8.如图,在长方体ABCD−A1B1C1D1中,AB=3,BC=CC1=2,点P在矩形BCC1B1内运动(包括边界),M,N分别为BC,CC1的中点,若A1P//平面MAN,当A1P取得最小值时,异面直线BP与DD1所成角的余弦值为( )
A. 55B. 2 55C. 1010D. 3 1010
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知{e1,e2}是平面内的一个基底,则下列也是平面内一个基底的是( )
A. {2e1−e2,−4e1+2e2}B. {2e1−e2,2e2}
C. {e1−e2,2e1−2e2}D. {e1−e2,e1+e2}
10.中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,AA1垂直于底面,AA1=5,底面扇环所对的圆心角为π2,弧AD的长度是弧BC长度的3倍,CD=2,则下列说法正确的是( )
A. 弧AD长度为32π
B. 曲池的体积为10π3
C. 曲池的表面积为20+14 π
D. 三棱锥A−CC1D的体积为5
11.在△ABC中,a,b,c分别为A,B,C的对边,则下列叙述正确的是( )
A. 若bcsC+ccsB=b,则△ABC是等腰三角形.
B. 若A>B,则cs2A
D. 若角C为钝角,则a3+b3
12.△ABC中,角A,B,C的对边分别为a,b,c,若sinA:sinB:sinC=2:3:4,则sinC= ______.
13.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB与MP是异面直线的序号是______;能得出AB//面MNP的图形的序号是______(写出所有符合要求的图形序号①②③④).
14.已知函数f(x)= 2|csπ2x|(x≥0),设函数f(x)图象的最高点从左至右依次为A0,A1,A2,…,f(x)与x轴的交点从左至右依次为B0,B1,B2,…,在线段A2B2上取10个不同的点C1,C2,C3,…,C10,则OA1⋅OC1+OA1⋅OC2+…+OA1⋅OC10= ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
如图,四棱锥P−ABCD中,底面ABCD为梯形,AB//CD,AB=4,CD=2,点M在棱PD上.
(1)求证:CD//平面PAB;
(2)若PB//平面MAC,求PMMD的值.
16.(本小题15分)
如图,在△ABC中,AD=25AB,点E为AC中点,点F为BC上的三等分点,且靠近点C,设CA=a,CB=b.
(1)用a,b表示EF,CD;
(2)如果∠ACB=60°,AC=2,且CD⊥EF,求|CD|.
17.(本小题15分)
在①bcsA−c=0,②acsB=bcsA,③acsC+b=0这三个条件中选择符合题意的一个条件,补充在下面的问题中,并求解.
在△ABC中,角A,B,C的对边分别为a,b,c,已知b= 2,c=4,满足____.
(1)请写出你的选择,并求出角A的值;
(2)在(1)的结论下,已知点D在线段BC上,且∠ADB=3π4,求CD长.
18.(本小题17分)
如图,在平面四边形ABCD中,AD⊥CD,AB⊥AC,AB=2 3.
(1)若∠ABC=30°,CD= 3AD,求BD的长;
(2)若AC=2,∠ADB=30°,求sin∠CAD的值.
19.(本小题17分)
如图正方体ABCD−A1B1C1D1的棱长为2,E是线段AA1的中点,平面α过点D1、C、E.
(1)画出平面α截正方体所得的截面,并简要叙述理由或作图步骤;
(2)求(1)中截面多边形的面积;
(3)平面α截正方体,把正方体分为两部分,求较小的部分与较大的部分的体积的比值.
答案和解析
1.【答案】D
【解析】解:由题意知a⊥b,所以−x+4×2=0,解得x=8.
故选:D.
根据向量垂直的坐标运算即可求解.
本题主要考查向量垂直的性质,属于基础题.
2.【答案】C
【解析】解:对于A,若m//n,n//α,则m//α或m⊂α,故A错误;
对于B,若α//β,l//α,则l//β或l⊂β,故B错误;
对于C,若α//β,l⊂α,则l//β,C正确;
对于D,少了m与n相交的条件,故D错误.
故选:C.
根据空间中的点线面的位置关系即可结合选项逐一求解.
本题考查直线与平面平行的性质的应用及平面与平面平行的性质的应用,属于基础题.
3.【答案】A
【解析】解:∵a=2,B=π3,△ABC的面积等于2 3,
∴12acsinB=12×2×c× 32=2 3,解得c=4,
∵由余弦定理可得b2=a2+c2−2accsB=4+16−2×2×4×12=12,
∴b=2 3.
故选:A.
由已知利用三角形的面积公式可求c的值,进而根据余弦定理即可求解b的值.
本题主要考查了三角形的面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.
4.【答案】B
【解析】解:以C为坐标原点,CD,CA所在直线分别为x,y轴建立如图所示的坐标系,
由题意得AC=2 2,则A(0,2 2),B( 2, 2),C(0,0),D(−2,0),AB=( 2,− 2),AC=(0,−2 2),DB=( 2+2, 2),所以 2+2= 2λ 2=− 2λ−2 2μ,
解得λ= 2+1μ=−1− 22,所以λ+μ= 22.
故选:B.
首先建立平面直角坐标系,进一步利用向量的坐标运算求出结果.
本题考察的知识点:向量的坐标运算,平面直角坐标系,主要考查学生的运算能力,属于中档题.
5.【答案】D
【解析】解:正方体的体积为23,挖去两个圆锥的体积为2×78(13π×12×2),
∴剩余几何体的体积为23−2×78×(13×π×12×2)=8−7π6,
故选:D.
利用空间几何体的体积公式可计算结果.
本题考查空间几何体的体积公式,属基础题.
6.【答案】B
【解析】解:因为e是单位向量,且|2e−a|= 10,
所以4e2−4a⋅e+a2=10,即a2−4a⋅e=6,
因为a+2e在e上的投影向量为5e,
所以(a+2e)⋅e|e|⋅e|e|=5e,
所以(a+2e)⋅e=5,即a⋅e=3,所以a2=18,即|a|=3 2,
所以cs
因为
故选:B.
由平面向量的数量积与投影等知识结合条件建立方程即可求得a⋅e和|a|,再由平面向量的夹角公式计算即可.
本题考查平面向量的数量积与夹角,投影向量等,属于基础题.
7.【答案】B
【解析】解:设OB=h,因为∠PBO=60°,则OP=OBtan60°= 3h,
因为∠PAO=30°,∠PCO=45°,
所以OA=OPtan30∘= 3h 33=3h,OC=OPtan45∘= 3h,
在△OBC中,OC2=OB2+BC2−2OB⋅BC⋅cs∠OBC,即3h2=h2+752−2×75hcs∠OBC,①
在△OAB中,OA2=OB2+AB2−2OB⋅AB⋅cs∠OBA,即9h2=h2+752−2×75hcs∠OBA,②
因为∠OBC+∠OBA=π,则cs∠OBC+cs∠OBA=0,
所以①②两式相加可得:12h2=2h2+2×752,解得:h=15 5,
则OP= 3h=15 15.
故选:B.
设OB=h,由题意可求得OP= 3h,OA=3h,OC= 3h,在△OBC中,OC2=OB2+BC2−2OB⋅BC⋅cs∠OBC,在△OAB中,OA2=OB2+AB2−2OB⋅AB⋅cs∠OBA,因为cs∠OBC+cs∠OBA=0,所以两式相加可解得h,即可得出OP.
本题主要考查解三角形,考查转化能力,属于中档题.
8.【答案】D
【解析】解:如图,取BB1的中点E,B1C1的中点F,连接EF,A1E,A1F,所以EF//BC1,
又M,N分别为BC,CC1的中点,所以MN//BC1,
故EF//MN,EF⊄平面MAN,所以EF//平面MAN,
又AA1//MF,AA1=MF,所以四边形A1AMF为平行四边形,故A 1F//AM,
A1F⊄平面MAN,A1F//平面MAN,
又A1F,EF⊂平面A1EF,A1F∩EF=F,故平面A1EF//平面MAN,
所以当A1P⊂平面A1EF时,A1P//平面MAN,则点P在线段EF上,
当A1P⊥EF时,A1P取得最小值,易知|A1E|=|A1F|= 9+1= 10,
则此时P为线段EF的中点.(等腰三角形中三线合一)
由DD1//BB1可得,所以∠B1BP为异面直线BP与DD1所成的角,
且由平面几何知识可知,|BE|=1,|EP|= 22,|BP|= 102,
cs∠B1BP=|BE|2+|BP|2−|EP|22|BE|×|BP|=3 1010.
所以异面直线BP与DD1所成角的余弦值为3 1010.
故选:D.
根据A1P//平面MAN,判断出点P的轨迹,然后求出A1P取得最小值时对应的P点的位置,根据异面直线所成角的定义算出答案.
本题考查异面直线所成角、线面平行、面面平行的判定与性质等基础知识,考查运算求解能力,是中档题.
9.【答案】BD
【解析】解:对于A,由于2e1−e2=−12(−4e1+2e2),
故2e1−e2,−4e1+2e2共线,不能成为基底;
对于B,设2e1−e2=2λe2,则λ不存在,
故2e1−e2,2e2不共线,可以作为基底;
对于C,由于e1−e2=12(2e1−2e2),
所以e1−e2,2e1−2e2共线,故不可以作为基底;
对于D,设e1−e2=μ(e1+e2),则μ不存在,
故e1−e2,e1+e2不共线,可以作为基底.
故选:BD.
根据向量是否共线即可结合选项判断.
本题考查向量共线的判定,属基础题.
10.【答案】ACD
【解析】解:设弧AD所在圆的半径为R,弧BC所在圆的半径为r,
因为弧AD长度是弧BC长度的3倍,底面扇环所对的圆心角为π2,
所以π2R=3×π2r,即R=3r;
所以CD=R−r=2r=2,解得:r=1,R=3,
所以弧AD长度为32π,选项A正确;
该曲池的体积为V=(14πR2−14πr2)⋅AA1=(9π4−π4)×5=10π,选项B错误;
曲池的表面积为S=(14×2πR+14×2πr)⋅AA1+2×CD⋅AA1+2×14π(R2−r2)=π2×(3+1)×5+2×2×5+π2×8=20+14π,选项C正确;
三棱锥A−CC1D的体积为VA−CC1D=13S△CD1D⋅R=13×12×2×5×3=5,选项D正确.
故选:ACD.
设弧AD所在圆的半径为R,弧BC所在圆的半径为r,根据题意列方程组求出R、r,再判断选项中的命题是否正确.
本题考查了简单几何体的结构特征应用问题,也考查了推理与运算能力,是基础题.
11.【答案】ABD
【解析】解;对于A,因为bcsC+ccsB=b,
由正弦定理得sinBcsC+sinCcsB=sinB,
在三角形中,sin(B+C)=sinB,
所以sinA=sinB,由正弦定理得a=b,
所以△ABC是等腰三角形,故A正确;
对于B,若A>B,则a>b,
由正弦定理得sinA>sinB>0,所以sin2A>sin2B,
即1−cs2A2>1−cs2B2,所以cs2A
因为asinA=bsinB,所以sinB=bsinAa=34,
因为b>a,所以B>A,
而12<34<12,所以30°
对于D,因为角C为钝角,所以c2>a2+b2,所以c>a,c>b,
即c3>ca2+cb2>a3+b3,故D正确.
故选:ABD.
对于A,利用正弦定理化边为角,再结合两角和的正弦公式及三角形内角和定理即可判断;对于B,根据大角对大边,再根据正弦定理化边为角,结合降幂公式即可判断;对于C,利用正弦定理求解即可;对于D,由题意可得c2>a2+b2,再结合不等式的性质即可判断.
本题考查正弦定理,余弦定理的应用,属于中档题.
12.【答案】 154
【解析】解:△ABC中,若sinA:sinB:sinC=2:3:4,
则由正弦定理有a:b:c=2:3:4,
不妨设a=2k,b=3k,c=4k(k>0),
则有csC=a2+b2−c22ab=4k2+9k2−16k212k2=−14,
由C∈(0,π),得sinC= 1−cs2C= 1−116= 154.
故答案为: 154.
由正弦定理有a:b:c=2:3:4,利用余弦定理求出csC,同角三角函数的平方关系求sinC.
本题考查了正弦定理,余弦定理以及同角三角函数基本关系式在解三角形中的应用,属于基础题.
13.【答案】①②④ ①③
【解析】解:在①中,取棱的中点E,如图所示:连接NE,ME,
由正方体性质得到EN//AB,
因为AB⊄平面MNPE,EN⊂平面MNPE,所以AB//平面MNP,
因为PM与EN相交,所以AB与MP是异面直线;
②若下底面中心为O,则NO//AB,NO∩面MNP=N,
所以AB与面MNP不平行,且AB与MP是异面直线;
③因为P,M是棱的中点,在正方体中,可得PM//AB,PM⊂平面PMN,
AB⊄平面PMN,AB//平面MNP,
④中,取棱的中点E,连接PE,如图所示:
在正方体中,可得PE//AB,
PE与PM相交,所以AB与PM是异面直线,
所以AB与平面MNP不平行.
故答案为:①②④;①③.
能得出AB//面MNP,关键是看平面MNP中有没有与AB平行的直线,或者有没有过AB的平面与平面MNP平行,逐一判断即可.
本题考查直线与平面平行的判定,是中档题.
14.【答案】100
【解析】解:先作出函数f(x)的图象如右图所示,
根据三角函数图象与性质易,得A1(2, 2),A2(4, 2),B2(5,0),
根据两点之间斜率坐标公式,得kOA1= 2−02−0= 22,kA2B2= 2−04−5=− 2,
因为kOA1⋅kA2B2=−1,所以OA1⊥A2B2,
设∠A1OB0=θ,根据直线倾斜角与斜率之间的关系,得kOA1=tanθ= 22,
因为θ为锐角,根据同角三角函数之间的关系,得csθ= 63,
延长OA1和B2A2交于点D,则OD=OB2⋅csθ=5 63,
那么向量OCi(1≤i≤10)在向量OA1上的投影为OD=5 63,
于是根据平面向量数量积的几何意义,得OA1⋅OC1+OA1⋅OC2+…+OA1⋅OC10=10,|OA1||OD|=10⋅ 22+( 2)2⋅5 63=100.
故答案为:100.
先作出函数f(x)的图象,得到A1(2, 2),A2(4, 2),B2(5,0),求出kOA1和kA2B2,根据斜率之间的关系可得OA1⊥A2B2,延长OA1和B2A2交于点D,进而得到向量OCi(1≤i≤10)在向量OA1上的投影为OD,再根据平面向量数量积的几何意义即可得结果.
本题考查三角函数的图象与性质,平面向量数量积的几何意义,考查了数形结合思想与转化思想,属于中档题.
15.【答案】(1)证明:因为CD//AB,且CD⊄平面PAB,AB⊂平面PAB,所以CD//平面PAB;
(2)解:连结BD交AC于点O,连结OM,
因为PB//平面MAC,且PB⊂平面PBD,平面PBD∩平面MAC=MO,所以PB//MO,
所以△DOM~△DBP,所以PMMD=OBOD,
因为CD//AB,所以△COS~△AOB,
故OBOD=ABCD=2,
所以PMMD=2.
【解析】(1)由CD//AB,结合线面平行的判定定理证明即可;
(2)连结BD交AC于点O,连结OM,利用线面平行的性质定理可得PB//MO,再利用△DOM~△DBP和△COS~△AOB,由相似比即可得到答案.
本题考查了平面平行的判定定理和性质定理的应用,同时考查了相似三角形的相似比的应用,考查了空间想象能力与逻辑推理能力,属于基础题.
16.【答案】解:(1)因为AD=25AB,点E为AC中点,点F为BC的三等分点,且靠近点C,
所以EF=EC+CF=−12CA+13CB=13b−12a,
CD=CA+AD=CA+25AB=CA+25(CB−CA)=35CA+25CB=25b+35a.
(2)由(1)可知,CD⋅EF=(25b+35a)⋅(13b−12a)=0,
所以215b2−310a2=0,由|a|=2,可得|b|=3,
所以|CD|= CD2= (25b+35a)2= 925a2+1225a⋅b+425b2= 3625+1225×2×3×12+3625=6 35.
【解析】(1)利用向量的加减法法则结合图形求解;
(2)由CD⊥EF,可得CD⋅EF=0,从而可得215b2−310a2=0,结合已知可得|b|=3,从而可求出|CD|.
本题考查了平面向量基本定理,向量共线,向量模的求法等知识点,重在培养学生数学运算,逻辑推理,直观想象的数学素养,属中档题.
17.【答案】解:(1)若选条件①,则有csA=cb=4 2=2 2>1,不合题意;
若选条件②,由余弦定理可得a⋅a2+c2−b22ac=b⋅b2+c2−a22bc,整理得a=b,
又因为此时a+b=2 2<4,不符合题意;
若选条件③,由余弦定理可得a⋅a2+b2−c22ab+b=0,即a2+3b2−c2=0,
所以a2=c2−3b2=16−6=10,
则csA=b2+c2−a22bc=2+16−102× 2× 10= 22,
因为A∈(0,π),所以A=π4;
故(1)答案选:③;
(2)由(1)的csC=b2+a2−c22ab=2+10−162× 2× 10=− 55,
因为c∈(0,π),则sinC= 1−cs2C=2 55,
sin∠CAD=sin(34π−C)=sin34πcsC−cs34πsinC= 1010,
在△ACD中,因为ACsin∠ADC=CDsin∠CAD,
则CD=ACsin∠CADsin∠ADC= 2× 1010 22= 105.
【解析】(1)依次代入条件①②③,可得①②不成立,故只能选③;
(2)由(1)结论再结合余弦定理可得csC,进而得到sinC,结合两角和差公式得到sin∠CAD,利用正弦定理得到CD.
本题考查正余弦定理的应用,属于中档题.
18.【答案】解:(1)在Rt△ABC中,∠ABC=30°,
则AC=ABtan∠ABC=2
在Rt△ACD中,tan∠CAD=CDAD= 3,
所以∠CAD=60°,
所以AD=AC·cs∠CAD=1,∠BAD=150°,
在△ABD中,由余弦定理可得BD2=AB2+AD2−2AB·AD·cs∠BAD=19,
所以BD= 19.
(2)设∠CAD=θ,则∠ABD=60°−θ,AD=2csθ,
在△ABD中,由正弦定理可得2csθsin(60∘−θ)=2 3sin30°,
化简得:csθ= 32sinθ,
由sin2θ+cs2θ=1,
可得:sin2θ=47,
又θ为锐角,所以sinθ=2 77,即sin∠CAD=2 77.
【解析】本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式在解三角形中的综合应用,考查了数形结合思想和转化思想,属于中档题.
(1)由已知可求在Rt△ACD中,tan∠CAD=CDAD= 3,可得∠CAD=60°,可求AD,在△ABD中,由余弦定理可得BD的值.
(2)设∠CAD=θ,则∠ABD=60°−θ,AD=2csθ,在△ABD中,由正弦定理可得csθ= 32sinθ,代入sin2θ+cs2θ=1,可得:sin2θ=47,结合θ为锐角,可求sin∠CAD的值.
19.【答案】解:(1)如图,取AB的中点F,连接EF、A1B、CF.
因为E是AA1的中点,所以EF//A1B.
在正方体ABCD−A1B1C1D1中,A1D1//BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,所以A1B//D1C,所以EF//D1C,
所以E、F、C、D1四点共面.
因为E、C、D1三点不共线,所以E、F、C、D1四点共面于平面α,
所以面EFCD1即为平面α截正方体所得的截面;
(2)由(1)可知,截面EFCD1为梯形,EF= AE2+AF2= 1+1= 2,
CD1= CD2+DD12= 4+4=2 2,D1E= A1D12+A1E2= 4+1= 5,
同理可得CF= 5,
如图所示:
分别过点E、F在平面CD1EF内作EM⊥CD1,FN⊥CD1,垂足分别为点M、N,
则D1E=CF,∠ED1M=∠FCN,∠EMD1=∠FNC=90°,
所以△EMD1≌△FNC,则D1M=CN,
因为EF//CD1,EM⊥CD1,FN⊥CD1,则四边形EFNM为矩形,
所以MN=EF= 2,所以D1M=CN=CD1−MN2=2 2− 22= 22,
所以EM= ED12−D1M2= 5−12=3 22,
所以梯形CD1EF的面积为S=12(EF+CD1)⋅EM=12×3 2×3 22=92;
(3)因为多面体AEF−DD1C为三棱台,
又S△AEF=12AE⋅AF=12×12=12,S△DD1C=12DD1⋅DC=12×22=2,
且该棱台的高为2,所以该棱台的体积为:
13(S△AEF+S△DD1C+ S△AEF⋅S△DD1C)⋅AD=13(12+2+ 12×2)×2=73,
故剩余部分的体积为8−73=173.
故较小的那部分与较大的那部分的体积的比值为717.
【解析】(1)取AB的中点F,连接EF、A1B、CF,利用平行线的传递性可证得EF//D1C,可知E、F、C、D1四点共面,再由于E、C、D1三点不共线,可得出面EFCD1即为平面截正方体所得的截面;
(2)分析可知,四边形CD1EF为等腰梯形,求出该等腰梯形的高,利用梯形的面积公式可求得截面面积;
(3)利用台体的体积公式可求得三棱台AEF−DD1C的体积,并求出剩余部分几何体的体积,由此可得结果.
本题考查立体几何的综合应用,正方体的截面问题,几何体的体积问题,属中档题.
2023-2024学年江苏省无锡市市北高级中学高一(下)期中数学试卷(含解析): 这是一份2023-2024学年江苏省无锡市市北高级中学高一(下)期中数学试卷(含解析),共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
江苏省无锡市辅仁高级中学2023-2024学年高一下学期3月月考数学试卷(解析版): 这是一份江苏省无锡市辅仁高级中学2023-2024学年高一下学期3月月考数学试卷(解析版),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年江苏省无锡市辅仁高级中学高一(下)月考数学试卷(3月份)(含解析): 这是一份2023-2024学年江苏省无锡市辅仁高级中学高一(下)月考数学试卷(3月份)(含解析),共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












