2024届中考冲刺阶段-中考真题（2023广州）及变式题-选择填空题部分（广州中考数学专用）

这是一份2024届中考冲刺阶段-中考真题（2023广州）及变式题-选择填空题部分（广州中考数学专用），文件包含冲刺2024中考真题及变式题-选择填空题部分广州中考数学专用答案docx、冲刺2024中考真题及变式题-选择填空题部分广州中考数学专用docx等2份试卷配套教学资源，其中试卷共86页， 欢迎下载使用。

试题难度适中，考查范围包括数与式、图形的变化、统计与概率、方程与不等式、函数、图形的性质。试题结构稳定，由易到难顺应学生的心理特征，易、中、难题分值比例兼顾学业水平与选拔功能，无偏题、怪题，基础占比合理，注重回归课本，夯实基础，全面考查学生的“四基”能力。
【2024中考考情预测】
针对选择填空题，在考前冲刺阶段，应特别注重基础，基础中档题尽量不丢分，这就需要回归课本，查漏补缺。同时，注重基础能力培养，狠抓细节，减少不必要的错误丢分。在此基础上，关注社会与经济发展、科学技术进步和多彩校园活动等，向“四能”和“九大数学核心素养”方向靠拢。
一、2023广州真题第1
1．（ ）
A．B．C．D．
二、变式题1
2．的相反数等于（ ）
A．B．C．D．±
3．相反数是5的数是（ ）
A．5B．C．D．
4．若一个数的相反数不是正数，则这个数一定是（ ）
A．正数B．非负数C．负数D．非正数
5．的值为（ ）
A．B．C．D．
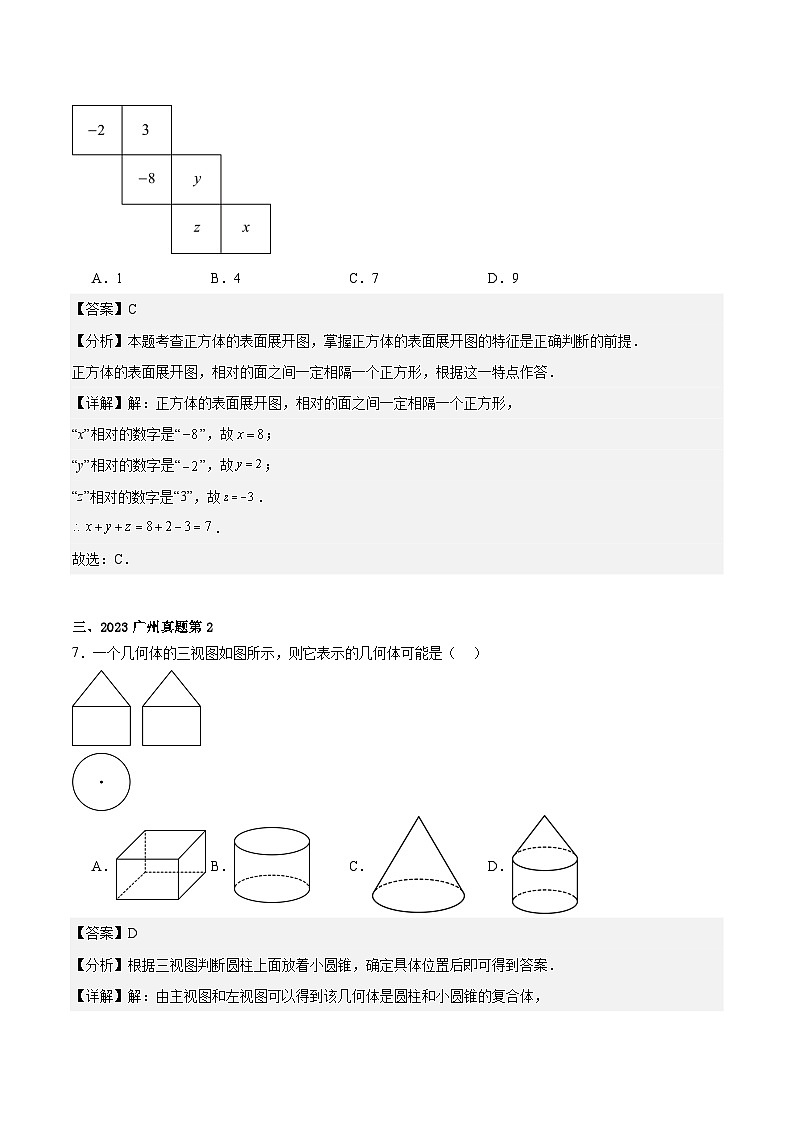
6．如图是一个正方体的表面展开图，如果相对面上所标的两个数互为相反数，那么的值是（ ）

A．1B．4C．7D．9
三、2023广州真题第2
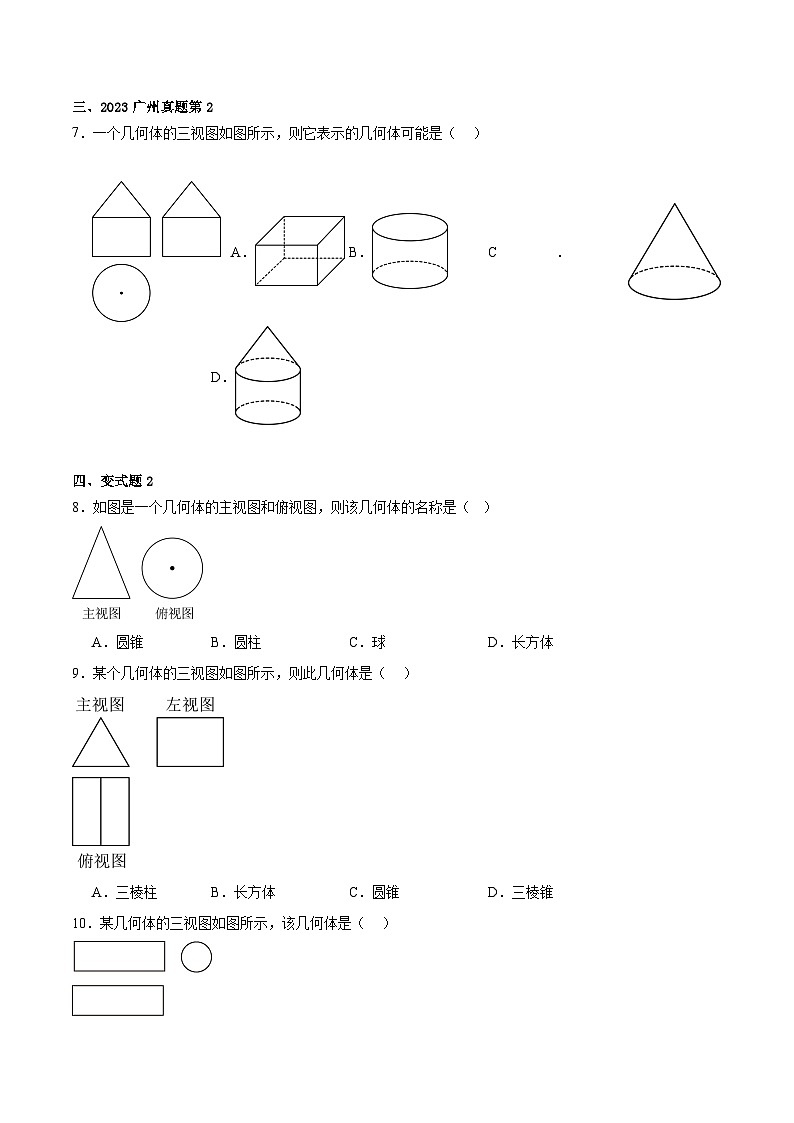
7．一个几何体的三视图如图所示，则它表示的几何体可能是（ ）
A．B．C．D．
四、变式题2
8．如图是一个几何体的主视图和俯视图，则该几何体的名称是（ ）
A．圆锥B．圆柱C．球D．长方体
9．某个几何体的三视图如图所示，则此几何体是（ ）

A．三棱柱B．长方体C．圆锥D．三棱锥
10．某几何体的三视图如图所示，该几何体是（ ）
A．圆柱B．正方体C．圆锥D．三棱柱
11．某几何体由一些大小相同的小正方体组成，如图分别是它的主视图和俯视图，那么要组成该几何体，至少需要多少个这样的小正方体（ ）
A．3B．4C．5D．6
12．某几何体的三视图如图所示，则它的表面展开图是（ ）
A．B．C．D．
五、2023广州真题第3
13．学校举行“书香校园”读书活动，某小组的五位同学在这次活动中读书的本数分别为10，11，9，10，12，下列关于这组数据描述正确的是（ ）
A．众数为10B．平均数为10C．方差为2D．中位数为9
六、变式题3
14．有一组统计数据：50、60、70、65、85、80、80．则对数据描述正确的是（ ）
A．中位数是65B．平均数80C．众数是80D．方差是85
15．一位卖“运动鞋”的经销商到一所学校对9位学生的鞋号进行了抽样调查．经销商最感兴趣的是这组数据中的（ ）
A．众数B．中位数C．平均数D．方差
16．一组数据：3，4，4，4，5，下列对这组数据的统计量说法错误的是（ ）
A．平均数是4B．中位数是4C．方差是4D．众数是4
17．某班进行演讲比赛，其中6人的成绩如下：，，，，，（单位：分），则下列说法不正确的是（ ）
A．这组数据的众数是分B．这组数据的方差是
C．这组数据的平均数是分D．这组数据的中位数是分
18．每年的6月6日是全国爱眼日，就在手机充斥着人们生活，占用大部分时间的同时，其蓝光危害以及用眼过度带来的影响也在悄然的威胁着人们的视力健康，某班为了解全班学生的视力情况，随机抽取了10名学生进行调查，将抽取学生的视力统计结果如下表．下列说法错误的是（ ）
A．平均数为4.7B．中位数为4.8
C．众数为4.8D．方差为0.0236
七、2023广州真题第4
19．下列运算正确的是（ ）
A．B．（）C．D．（）
八、变式题4
20．下列计算正确的是（ ）
A．B．C．D．
21．下列运算正确的是( )
A．B．C．D．
22．计算的结果是（ ）.
A．B．C．D．
23．下列运算正确的是（ ）
A．B．
C．D．
24．下列运算正确的是（ ）
A．B．
C．D．
九、2023广州真题第5
25．不等式组的解集在数轴上表示为（ ）
A． B．
C． D．
十、变式题5
26．将不等式组的解集表示在数轴上，正确的是（ ）．
A．B．
C．D．
27．解不等式组时，不等式①②的解集在同一条数轴上表示正确是（ ）
A． B．
C． D．
28．关于x的不等式组的解集，在数轴上表示正确的是（ ）
A． B．
C． D．
29．如图，数轴上表示的是某不等式组的解集，则这个不等式组可能是（ ）
A．B．C．D．
30．不等式组的解集在数轴上表示正确的是（ ）
A．B．
C．D．
十一、2023广州真题第6
31．已知正比例函数的图象经过点，反比例函数的图象位于第一、第三象限，则一次函数的图象一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
十二、变式题6
32．一次函数的图象经过（ ）
A．第一、二、三象限B．第二、三、四象限C．第一、二、四象限D．第二、三、四象限
33．如果当时，反比例函数的函数值随x的增大而增大，那么一次函数的图象经过（ ）
A．第一、二、三象限B．第一、二、四象限
C．第一、三、四象限D．第二、三、四象限
34．已知双曲线在二､四象限内，则直线的大致图像是（ ）
A．B．C．D．
35．反比例函数图像上有两个点，，，则的图像不经过第（ ）象限
A．一B．二C．三D．四
36．若反比例函数的图象如图所示，则一次函数的图象不经过（ ）

A．第一象限B．第二象限C．第三象限D．第四象限
十三、2023广州真题第7
37．如图，海中有一小岛A，在B点测得小岛A在北偏东30°方向上，渔船从B点出发由西向东航行10到达C点，在C点测得小岛A恰好在正北方向上，此时渔船与小岛A的距离为（ ）

A．B．C．20D．
十四、变式题7
38．如图，在坡角为30°的斜坡上要栽两棵树，要求它们之间的水平距离为，则这两棵树之间的坡面的长为（ ）
A．B．C．D．
39．如图，一棵垂直于地面的树在一次强台风中从高地面米处折断倒下，倒下部分与地面成角，这棵树在折断前的高度为（ ）
A．米B．米C．米D．米
40．如图所示，在距离铁轨的B处，观察由南京开往上海的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东方向上，后，动车车头到达C处，恰好位于B处的西北方向上，则这列动车的平均车速是（ ）
A．B．
C． D．
41．一艘渔船从港口沿北偏东60°方向航行60海里到达处时突然发生故障，位于港口正东方向的处的救援艇接到信号后，立即沿北偏东45°方向以40海里/小时的速度前去救援，救援艇到达处所用的时间为（ ）
A．小时B．小时C．小时D．小时
42．如图，在四边形ABCD中，，点P是四边形ABCD边上的一个动点．若点P到AC的距离为，则点P的位置有（ ）
A．1处B．2处C．3处D．4处
十五、2023广州真题第8
43．随着城际交通的快速发展，某次动车平均提速60，动车提速后行驶480与提速前行驶360所用的时间相同．设动车提速后的平均速度为x，则下列方程正确的是（ ）
A．B．C．D．
十六、变式题8
44．现代科技的发展已经进入5G时代，某地区将在2021年基本实现5G信号全覆盖．5G网络峰值速率为4G网络峰值速率的10倍，在峰值速率下传输4千兆数据，5G网络比4G网络快360秒，则由题意可列方程（ ）
A．B．C．D．
45．寒风乍起，甲安装队为A小区安装66台空调，乙安装队为B小区安装60台空调，两队同时开工且恰好同时完工，甲队比乙队每天多安装2台．设乙队每天安装x台，根据题意，下面所列方程中正确的是（ ）
A．B．C．D．
46．赛龙舟是端午节的主要习俗之一，也是中国民俗传统与运动精神的完美结合．2019年起，深圳大沙河生态长廊龙舟邀请赛连续4年举办，已然成为深圳市标志性的体育赛事．2022年龙舟邀请赛设置了标准龙舟（22人龙舟）500米直道竞速赛项目，其中甲、乙两队参加比赛（比赛起点相同），甲队每秒的速度比乙队快0.5米，结果甲队比乙队提前14秒到达终点．设甲队的速度为米/秒，下列方程正确的是（ ）
A．B．
C．D．
47．嘉嘉和淇淇两人同时从A地出发，骑自行车前往B地，已知A，B两地的距离为18km， ，并且嘉嘉比淇淇先到18分钟．若设淇淇每小时走x km，所列方程为，则横线上的信息可能为（ ）
A．嘉嘉每小时比淇淇多骑行3kmB．嘉嘉每小时比淇淇少骑行3km
C．嘉嘉和淇淇每小时共骑行3kmD．嘉嘉每小时骑行的路程是淇淇的3倍
48．课本习题：“A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？”下列四位同学列方程正确的是（ ）
①设A型机器人每小时搬运xkg化工原料，则：
甲列的方程为：；乙列的方程为：
②设A型机器人搬运900kg化工原料需要x小时，则：
丙列的方程为：；丁列的方程为：
A．甲、丙B．甲、丁C．乙、丙D．乙、丁
十七、2023广州真题第9
49．如图，的内切圆与，，分别相切于点D，E，F，若的半径为r，，则的值和的大小分别为（ ）
A．2r，B．0，C．2r，D．0，
十八、变式题9
50．如图，P为外一点，、分别切于点A、B，切于点E，分别交、于点C、D，若，则的周长为（ ）
A．8B．6C．12D．10
51．如图，△ABC中，内切圆I和边BC、AC、AB分别相切于点D、E、F，若∠B＝55°，∠C＝75°，则∠EDF的度数是（ ）
A．55°B．60°C．65°D．70°
52．如图，的内切圆与、、分别相切于点、、，且，，，则阴影部分（即四边形）的面积是（ ）

A．B．C．D．
53．如图，在中，，点在边上，过的内心作于点．若，，则的长为（ ）

A．6B．7C．8D．9
54．如图，的内切圆与，，相切于点，，，已知，，，，则的长是（ ）
A．B．C．D．
十九、2023广州真题第10
55．已知关于x的方程有两个实数根，则的化简结果是（ ）
A．B．1C．D．
二十、变式题10
56．若方程x2＋4x＋a＝0无实根，化简等于（ ）
A．4﹣aB．a﹣4C．﹣（a＋4）D．无法确定
57．已知关于x的一元二次方程2x2﹣x+m＝0有两个实数根，那么化简的结果为（ ）
A．m﹣1B．1﹣mC．±（m﹣1）D．m+1
58．关于x的一元二次方程无实数解，则k的取值范围是（ ）
A．B．C．D．
59．关于的方程有两个相等的实数根，则（ ）
A．B．C．D．
60．已知关于x的方程有实数根，则k的取值范围为（ ）
A．B．且C．且D．
二一、2023广州真题第11
61．近年来，城市电动自行车安全充电需求不断攀升．截至2023年5月底，某市已建成安全充电端口逾280000个，将280000用科学记数法表示为 ．
二二、变式题11
62．在比例尺为的地图上，量得两地在地图上的距离为厘米，即实际距离为28000000厘米．数据28000000用科学记数法可表示为 ．
63．“北斗系统”是我国自主建设运行的全球卫星导航系统，国内多个导航地图采用北斗优先定位．目前，北斗定位服务日均使用量已超过3600亿次．3600亿用科学记数法表示为 ．
64．向月球发射无线电波，无线电波到月球并返回地面需．已知无线电波每秒传播，则地球和月球之间的距离约是 ．
65．清代诗人袁枚创作了一首诗《苔》：“白日不到处，青春恰自来.苔花如米小，也学牡丹开”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒直径约为米，用科学记数法表示，则 .
66．福岛第一核电站核废水即便被海水稀释后放射量仍达到贝克勒尔，数据用科学记数法表示为 ．
二三、2023广州真题第12
67．已知点，在抛物线上，且，则 ．（填“<”或“>”或“=”）
二四、变式题12
68．抛物线经过点，．则m n（填“＞”，“=”或“＜”）．
69．如果点和点是抛物线（m常数）上的两点，那么 ．（填“>”、“=”、“<”）
70．已知点都在函数的图象上，则的大小关系为 ．
71．已知二次函数，当时，y的最小值为 ．
72．在平面直角坐标系中，已知点是抛物线上任意一点，则长的最小值为 ．
二五、2023广州真题第13
73．2023年5月30日是第7个全国科技工作者日，某中学举行了科普知识手抄报评比活动，共有100件作品获得一、二、三等奖和优胜奖，根据获奖结果绘制如图所示的条形图，则a的值为 ．若将获奖作品按四个等级所占比例绘制成扇形统计图，则“一等奖”对应扇形的圆心角度数为 ．

二六、变式题13
74．渌口中学的男生人数是女生人数的，男女学生人数制成扇形统计图，在扇形统计图上表示男生的扇形圆心角是 度．
75．七年级某个班学生全班参加社团活动课的扇形统计图如下图，那么扇形统计图中“其他”所占圆心角度数为 度．

76．某市各类学校占该市学校总数的百分比如下：
若根据这个统计表制作扇形统计图，则“中学”对应的扇形圆心角的度数为 ．
77．老师随机抽查了本学期学生阅读课外书册数的情况，并将抽查结果绘制成条形图（图1）和不完整的扇形图（图2），其中条形图被墨迹遮盖了一部分．总人数为 ；扇形图中5册所占的圆心角的度数为 ．
78．高尔基说：“书，是人类进步的阶梯”．阅读可以丰富知识，拓展视野，充实生活，给我们带来愉快．英才中学计划在各班设立图书角，为合理搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对全校学生进行抽样调查，收集整理喜爱的书籍类型（A．科普，B．文学，C．体育，D．其他）数据后，绘制出两幅不完整的统计图：
小亮根据这两幅不完整的统计图得出以下五个结论：①样本容量为400 ；②类型B的人数为120人；③类型C所占百分比为；④类型C所对应的扇形的圆心角为126°； ⑤类型D的人数是类型B的人数的．你判断一下小亮结论中错误的是 ． （请填写序号）
二七、2023广州真题第14
79．如图，正方形的边长为4，点E在边上，且，F为对角线上一动点，连接，，则的最小值为 ．

二八、变式题14
80．如图，四边形是正方形，点E是边上一点，且，且交正方形外角平分线于点F．若正方形边长是8，，则的长为 ．
81．如图，在边长为1的正方形中，E为边上一动点（点E，B不重合），以为直角边在直线上方作等腰直角三角形，，连接，则在点E的运动过程中，周长的最小值是 ．

82．四边形是正方形，E，F分别是和的延长线上的点，且，连接，，．若，，则的面积为 ．
83．如图，在△ABC中，∠C=90°，AC=4，BC=2，以AB为一条边向三角形外部作正方形ABDE，P为DE上一点，则四边形ACBP的面积为 ．
84．如图，正方形ABCD的边长为4，点M在AB上，且，N是BD上一动点，则的最小值为 ．
二九、2023广州真题第15
85．如图，已知是的角平分线，，分别是和的高，，，则点E到直线的距离为 ．

三十、变式题15
86．如图，AD是△ABC的角平分线，AB：AC=3：2，△ABD的面积为15，则△ACD的面积为 ．
87．如图，平分，．若，，则AB的长为 ．
88．如图，已知，O为和的平分线的交点，于点E，且，则AB与CD之间的距离是 .
89．如图，在边长为2的正方形中，，分别是边，上的动点（可与端点重合），，分别是，的中点，则的最大值为 ．
90．已知：如图，△ABC中，∠C＝90°，点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D、E、F分别是垂足，且AB＝10cm，BC＝8cm，CA＝6cm，则点O到三边AB、AC和BC的距离分别等于 ．
三一、2023广州真题第16
91．如图，在中，，，，点M是边上一动点，点D，E分别是，的中点，当时，的长是 ．若点N在边上，且，点F，G分别是，的中点，当时，四边形面积S的取值范围是 ．

三二、变式题16
92．如图，已知四边形中，，点分别是边的中点，连接，则的长是 ．

93．如图，矩形中，，，E是的中点，F是线段上一动点，P是的中点，连接，则线段的最小值为 ．

94．如图，在Rt△ABC中∠BAC＝90°，点D和点E分别是AB，AC的中点，点F和点G分别在BA和CA的延长线上，若BC＝10，GF＝6，EF＝4，则GD的长为 ．
95．在菱形ABCD中，∠D=60°，CD=4，E为菱形内部一点，且AE=2，连接CE，点F为CE中点，连接BF，取BF中点G，连接AG，则AG的最大值为 ．
96．如图，是线段上一点，和是位于直线同侧的两个等边三角形．若，则四边形的面积最小值是 ．
视力
4.5
4.6
4.7
4.8
4.9
5.0
人数
1
1
2
3
1
2
幼儿园
小学
中学
高等院校
其他