2024年中考数学精选压轴题之平行四边形与特殊的平行四边形

这是一份2024年中考数学精选压轴题之平行四边形与特殊的平行四边形，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每题3分，共36分）
1．如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（ ）
A．23+2B．5-33C．3-3D．3+1
2．如图，在四边形ABCD中，∠A=∠B=90°，AD=10cm，BC=8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是 （ ）
A．当 t＝4s 时，四边形 ABMP 为矩形
B．当 t＝5s 时，四边形 CDPM 为平行四边形
C．当 CD＝PM 时，t＝4s
D．当 CD＝PM 时，t＝4s 或6s
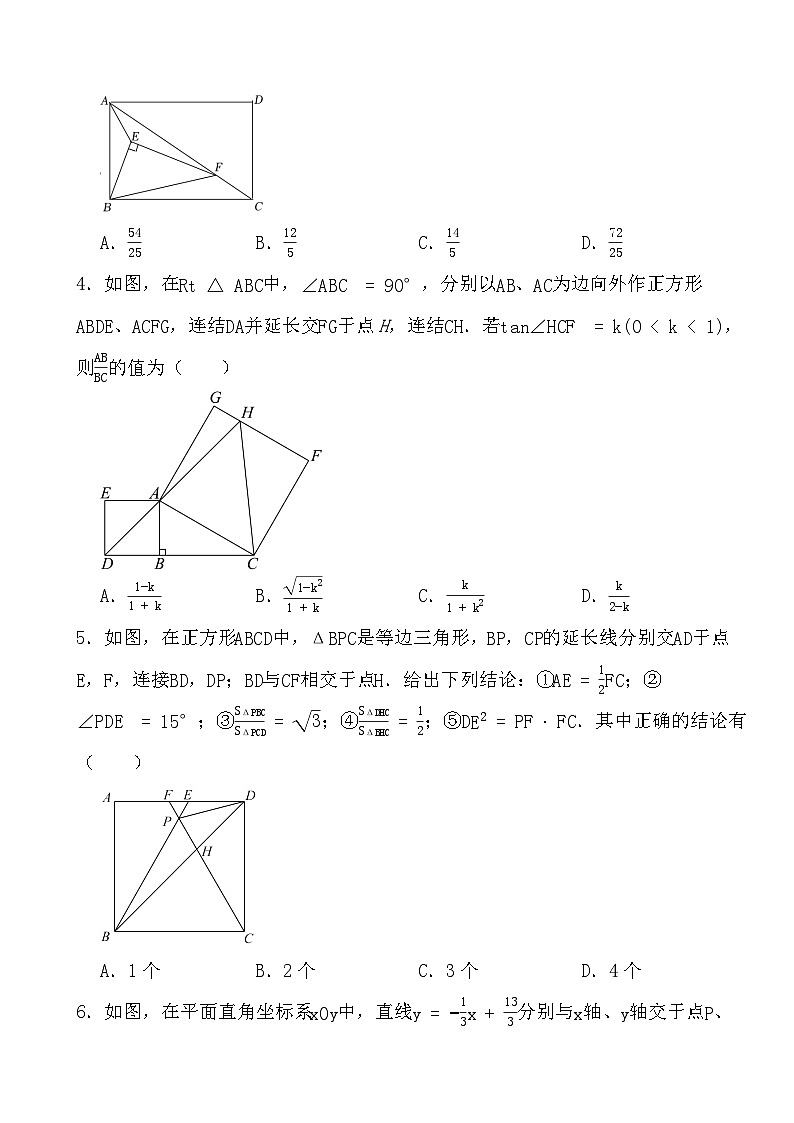
3．如图，直角三角形BEF顶点F在矩形ABCD的对角线AC上运动，连接AE．∠EBF=∠ACD，AB=6，BC=8，则AE的最小值为（ ）．
A．5425B．125C．145D．7225
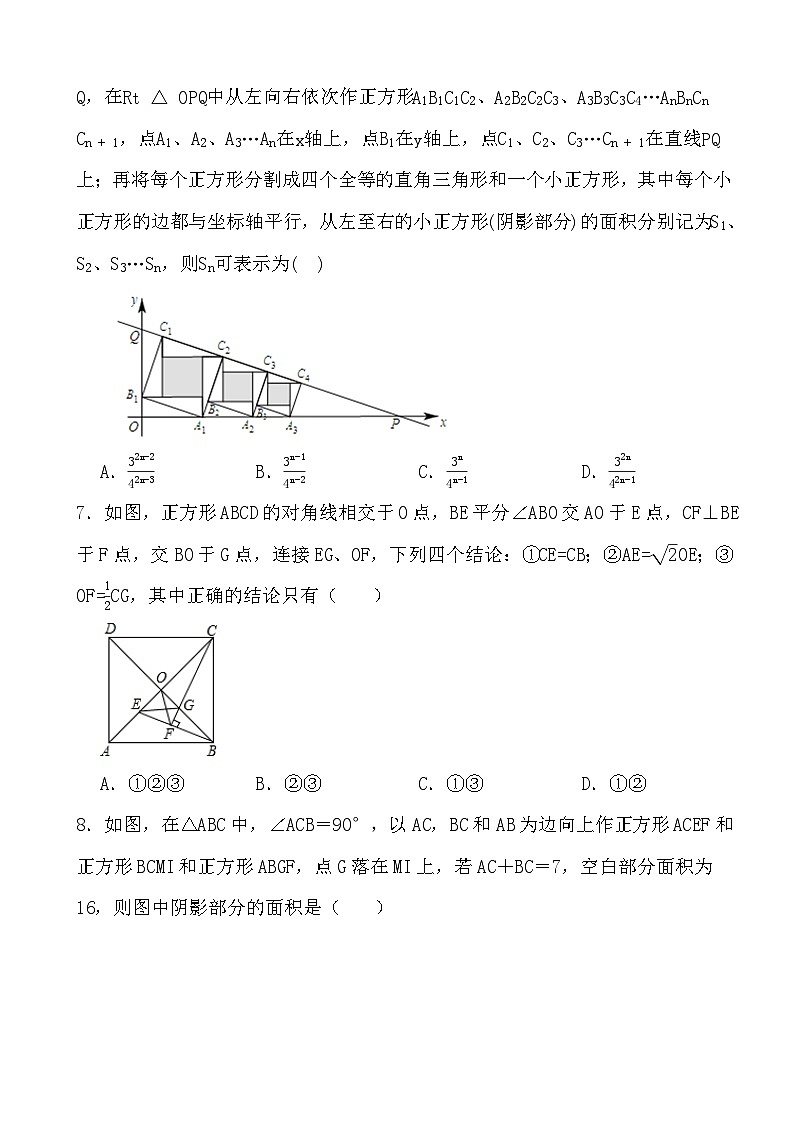
4．如图，在Rt△ABC中，∠ABC=90°，分别以AB、AC为边向外作正方形ABDE、ACFG，连结DA并延长交FG于点H，连结CH．若tan∠HCF=k(0A．1−k1+kB．1−k21+kC．k1+k2D．k2−k
5．如图，在正方形ABCD中，ΔBPC是等边三角形，BP，CP的延长线分别交AD于点E，F，连接BD，DP；BD与CF相交于点H．给出下列结论：①AE=12FC；②∠PDE=15°；③SΔPBCSΔPCD=3；④SΔDHCSΔBHC=12；⑤DE2=PF⋅FC．其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
6．如图，在平面直角坐标系xOy中，直线y=−13x+133分别与x轴、y轴交于点P、Q，在Rt△OPQ中从左向右依次作正方形A1B1C1C2、A2B2C2C3、A3B3C3C4…AnBnCnCn+1，点A1、A2、A3…An在x轴上，点B1在y轴上，点C1、C2、C3…Cn+1在直线PQ上；再将每个正方形分割成四个全等的直角三角形和一个小正方形，其中每个小正方形的边都与坐标轴平行，从左至右的小正方形(阴影部分)的面积分别记为S1、S2、S3…Sn，则Sn可表示为( )
A．32n−242n−3B．3n−14n−2C．3n4n−1D．32n42n−1
7．如图，正方形ABCD的对角线相交于O点，BE平分∠ABO交AO于E点，CF⊥BE于F点，交BO于G点，连接EG、OF，下列四个结论：①CE=CB；②AE=2OE；③OF=12CG，其中正确的结论只有（ ）
A．①②③B．②③C．①③D．①②
8．如图，在△ABC中，∠ACB＝90°，以AC，BC和AB为边向上作正方形ACEF和正方形BCMI和正方形ABGF，点G落在MI上，若AC＋BC＝7，空白部分面积为16，则图中阴影部分的面积是（ ）
A．16B．15C．665.D．995
9．如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接DF，分别交AE，AC于点G，M．P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM．有下列四个结论：
①AE垂直平分DM；②PM＋PN的最小值为32；③CF2＝GE•AE；④S△ADM＝62．
其中正确的是（ ）
A．①②B．②③④C．①③④D．①③
10．如图，在矩形ABCD中，ABA．34B．78C．89D．910
11．如图，把菱形ABCD向平移至DCEF的位置，作EG⊥AB，垂足为G，EG与CD相交于点M，GD的延长线交EF于点H，连接DE，则下列结论：①DG=DE；②∠DHE=12∠BAD；③EF+FH=2MC；④△CDE∽△DEH，则正确的结论有（ ）个
A．1B．2C．3D．4
12．如图，边长为22的正方形ABCD，对角线AC，BD相交于O，E为BC边上一动点（不与B，C重合），OF⊥OE交CD于F，G为EF中点．给出如下四个结论：①∠OEF＝45°；②点E在运动过程中，△OEF面积不变化；③△CEF周长的最小值为2+22；④点E在运动过程中，OG与CG始终相等，其中正确的结论是（ ）
A．①③B．②③C．①④D．①③④
二、填空题（每题3分，共18分）
13． 如图，在矩形ABCD中，E是AD的中点，连接BE，将△ABE沿着BE翻折得到△FBE，EF交BC于点H，延长BF，DC相交于点G，若DG=8，BC=12，则EH= ．
14．如图，正方形ABCD中，M、N分别是AD、BC边上的点，将四边形ABNM沿直线MN翻折，使得点A、B分别落在点A'、B'处，且点B'恰好为线段CD的中点，A'B'交AD于点G，作DP⊥MN于点P，交A'B'于点Q．若AG=8，则PQ= ．
15． 在菱形ABCD中，∠ABC=120°，点P是对角线BD上一动点，点Q是AD边上一动点，DP与AQ始终相等，连结AP、BQ，交点为E，连结CE，则tan∠DCE的最小值是 ．
16．如图，在长方形ABCD中，ΔAEF为等腰Rt△，且∠AEF=90°，点E在线段BC上，点F在线段CD上，若3(AB+BE)=2(AD+DF)，则SΔAEFS长方形ABCD= ．
17． 如图，在菱形ABCD中，E、F分别是 AB，BC边上的中点，G为 DE上一点，若 AB=4，∠B=∠EGF=60°，则DG的长为
18．如图，菱形ABCD中，AD=4，∠A=45°，DE⊥AB，垂足为E，点P在菱形的边上，若DE=DP，则CP的长为 ．
三、解答题（共6题，共46分）
19．如图，在平行四边形ABCD中，点E在BC边上，且AD=DE，F为线段DE上一点，且∠AFE=∠B.
（1）求证：∠AFD=∠ECD；
（2）求证：△AFD≅△DCE；
（3）若∠B=60°，CD=DF，BE=2，连结AE，求AE的长度.
20．如图①，在平行四边形ABCD中，AB=2，BC=22，∠B=45°，点E为BC中点，动点P从点E出发，沿折线EB−BA以每秒2个单位长度的速度运动．作∠PEQ=90°，EQ交边AD或边DC于点Q，连接PQ．当点P与点A重合时，点P停止运动．设点P的运动时间为t秒．（t>0）
（1）当P在AB上运动时，用含t的式子表示出线段BP的长 ；
（2）当Q落在CD的中点时，求t的值；
（3）若Q不与顶点重合，当Q落在平行四边形ABCD的某一内角平分线上时，求tan∠BEP的值；
（4）作点E关于直线PQ的对称点F，连接PF、QF，当四边形EPFQ和平行四边形ABCD重叠部分图形为轴对称四边形时，直接写出t的取值范围．
21． 已知△ABC和△ADE都是等腰三角形，且AB=AC，AD=AE，若点D在BC边上运动时，总保持∠ADE=∠B，连接CE,DE与AC交于点F．
（1）①如图1，当点D为BC边中点时，则CEBC的值为 ▲ ；
②如图2，当点D不为BC边中点时，求证：CE=BD；
（2）如图3，当点D在BC边上运动中恰好使得AE∥BC时，若AB=5，BC=6，求DF的长．
22．如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A出发沿AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动，当其中一点到达终点运动即停止．设运动时间为t秒．
（1）在运动过程中，PQ的长度能否为35cm？若能，求出t的值，若不能，请说明理由；
（2）在运动过程中，△PDQ的面积能否为8cm2？若能，求出t的值，若不能，请说明理由；
（3）取PQ的中点M，运动过程中，当∠AMD=90°时，求t的值；
23．已知：在矩形ABCD中，把矩形ABCD绕点C旋转，得到矩形FECG，且点E落在AD边上，连接BG交CE于点H．
（1）如图1，连接BE．
①求证：BE平分∠AEC；
②求证：H是BG的中点；
（2）如图2，连接FH，若FH平分∠EFG，CH=2，求AE的长．
24．
（1）如图1，已知正方形AEFG与正方形ABCD，将正方形AEFG绕点A按逆时针方向旋转，求证：BE=DG，且BE⊥DG；
（2）如图2，将（1）中的两个正方形分别改成矩形AEFG和矩形ABCD，且AEAG=ABAD=23，AE=2，AB=4，将矩形AEFG绕点A顺时针方向旋转，连接DE，BG，在旋转过程中，DE2+BG2的值是定值，请求出这个定值．
答案解析部分
1．【答案】D
2．【答案】D
3．【答案】D
4．【答案】D
5．【答案】D
6．【答案】A
7．【答案】A
8．【答案】D
9．【答案】D
10．【答案】D
11．【答案】D
12．【答案】D
13．【答案】2116
14．【答案】1855
15．【答案】23−62
16．【答案】512
17．【答案】1077
18．【答案】22或4−22或210
19．【答案】（1）证明： ∵四边形ABCD是平行四边形，
∴∠B+∠ECD=180°；
∵∠AFE=∠B，∠AFE+∠AFD=180°，
∴∠AFD=∠ECD.
（2）证明：∵四边形ABCD是平行四边形
∴AD∥BC，
∴∠ADF=∠DEC，
由（1）知：∠AFD=∠ECD，
∵AD=DE，
∴△AFD≌△DCE(AAS).
（3）解：∵△AFD≌△DCE，
∴AF=CD；
∵CD=DF，
∴AF=DF，
∵∠B=∠AFE=60°，
∴∠ADF=∠DAF=30°；
∵AD=DE，
∴∠DAE=∠DEA=75°，
∴∠EAG=45°；
∵四边形ABCD是平行四边形
∴AD∥BC，
∴∠DAE=∠AEB，
∴∠DEA=∠AEB；
∵∠AFE=∠B，AE=AE，
∴△ABE≌△AFE，
∴EF=BE=2；
如图，过E作EG⊥AF于G，
则∠AEG=∠EAG=45°，
∴AE=EG，∠GEF=∠AEF−∠AEG=30°；
在Rt△EGF中，FG=12EF=1，由勾股定理得EG=EF2−FG2=3，
在Rt△EGA中，AG=EG=3，由勾股定理得AE=AG2+EG2=6．
20．【答案】（1）2t−2
（2）解：t=1+324（过程略）
（3）解：2或2−2
（4）解：t=021．【答案】（1）解：①12
②证明：由①知，∠BAD=∠CAE．
在△BAD和△CAE中，AB=AC∠BAD=∠CAEAD=AE，
∴△BAD≌△CAE(SAS)，
∴CE=BD；
（2）解：∵AE∥BC，
∴∠AED=∠CDE，∠DCA=∠EAC，
∵∠ADE=∠AED=∠B=∠ACB，
∴∠ADE=∠CDE=∠B，
∴AB∥DE，
∴四边形ABDE为平行四边形，∠BAD=∠ADE，
∴∠BAD=∠B=∠ACB，DE=AB=5，
∴△ABD∽△CBA．
∴BDAB=ABBC，即BD5=56．
∴BD=256．
∴CD=BC−BD=116，AE=BD=256．
∵AE∥BC，
∴△AFE∽△CFD，
∴DFEF=CDAE=1125，
∴DF=1136DE=1136×5=5536．
22．【答案】（1）解：PQ的长度能为35cm，理由如下：
根据题意可知：AP=tcm，BP=AB−AP=(6−t)cm，BQ=2tcm，
∵四边形ABCD是矩形，
∴∠B=90°，
在Rt△BPQ中，BP2+BQ2=PQ2，
∴(6−t)2+(2t)2=(35)2，
解得：t=−53（舍去）或t=3，
∴当t为−53或3时，PQ的长度为35cm ；
（2）解：△PDQ的面积不能为8cm2，理由如下：
设运动x秒钟后△PDQ的面积为8cm2，
则AP=xcm，BP=(6−x)cm，BQ=2xcm，CQ=(12−2x)cm，
S△PDQ=S矩形ABCD-S△ADP-S△CDQ-S△BPQ
=AB⋅BC−12AD⋅AP−12CD⋅CQ−12BP⋅BQ，
=6×12−12×12x−12×6(12−2x)−12(6−x)⋅2x
=x2−6x+36
=8，
即x2−6x+36=8，
∴x2−6x+28=0，
∴Δ=b2−4ac=36−4×28<0
∴方程无实数根，
∴△PDQ的面积不能为8cm2；
（3）解：如图，以B为坐标原点，BC所在直线为x轴，建立平面直角坐标系，
设P(0,6−t)，Q(2t,0)，
∴M(t,3−12t)，
又∵A(0,6)，D(12,6)，
∴取AD的中点N(6,6)，连接MN，则AD=12，
∵∠AMD=90°，
∴MN=12AD=6，
∴(t−6)2+(3−12t−6)2=62，
解得：t1=6，t2=65．
23．【答案】（1）证明①如图，
由旋转性质得EC=BC，
∴∠CEB=∠CBE，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠AEB=∠CBE，
∴∠AEB=∠CEB，
∴BE平分∠AEC；
②如图，过点B作BP⊥CE于点P，
由①可知∠AEB=∠CEB，
又∵∠A=∠BPE，且BE=BE，
∴△AEB≌△PEB(AAS)，
∴BP=BA，
∵BA=DC=GC，
∴BP=GC，
又∵∠BHP=∠GHC，∠BPH=∠GCH=90°，
∴△BPH≌△GCH(AAS)，
∴BH=HG，
∴点H为BG中点，
（2）解：如图，作BP⊥CE于点P，
由（1）可知△AEB≌△PEB，△BPH≌△GCH，
∴AE=PE，PH=CH=2，
∵∠EFG=∠FEH=90°，FH平分∠EFG，
∴∠EFH=12∠EFG=45°
∴∠EHF=45°=∠EFH，
∴EF=EH=BA=DC，
设AE=PE=x，则EC=x+4，EH=x+2，
∴BC=EC=AD=x+4，EF=EH=BA=DC＝x+2，
∴ED=AD−AE=4，
∵∠EDC=90°，
∴(x+2)2+42=(x+4)2，
解得x=1，
∴AE=1．
24．【答案】（1）证明：如图，延长DG交BE于H，交AB于M，
∵四边形AEFG与四边形ABCD是正方形，
∴AE=AG，
AB=AD，
∠EAG=∠BAD=90°，
∴∠BAE+∠BAG=∠DAG+∠BAG，
∴∠BAE=∠DAG，
在△BAE和△DAG中
AE=AG∠BAE=∠DAGAB=AD，
∴△BAE≌△DAG（SAS），
∴BE=DG，∠ABE=∠ADG，
∴∠AMG+∠ADG=90°，
∵∠AMG=∠BMH，
∵∠ABE+∠BMH=90°，
∴∠BHM=90°，
∴BE⊥DG；
（2）解：如图，连接EG、BD，DG交BE于P，DG交AB于N，
∵四边形AEFG和四边矩形ABCD是矩形，
∴∠EAG=∠BAD=90°，
∴∠EAG+∠BAG=∠BAD+∠BAG，
∴∠BAE=∠DAG，
∵AEAG=ABAD=23，
AE=2，AB=4，
∴△BAE∽△DAG，AG=3，AD=6，
∴∠ABE=∠ADG，
∴∠ADG+∠AND=90°，
∵∠AND=∠BNP，
∴∠ABE+∠BNP=90°，
∴∠BPN=90°，
∴BE⊥DG，
EG2=AE2+AG2=22+32=13，
BD2=AD2+AB2=42+62=52，
DE2=PE2+PD2，
BG2=PB2+PG2，
∴DE2+BG2
=PE2+PD2+PB2+PG2
=(PE2+PG2)+(PD2+PB2)
=EG2+BD2
=13+52
=65．