中考数学一轮复习课件圆的有关概念及性质

这是一份中考数学一轮复习课件圆的有关概念及性质，共28页。PPT课件主要包含了圆的有关概念，两条弧，垂径定理及其推论，弦圆心角的关系，圆内接四边形，应用意识等内容，欢迎下载使用。

圆的有关性质(常考点)
1.圆是轴对称图形,任何一条　 　所在的直线都是圆的对称轴.圆既是中心对称图形,又是旋转对称图形,即圆具有旋转不变性.圆心就是它的对称中心. 2.垂径定理及其推论(1)垂径定理:垂直于弦的直径　 　弦,并且平分弦所对的两条弧(如图所示). 
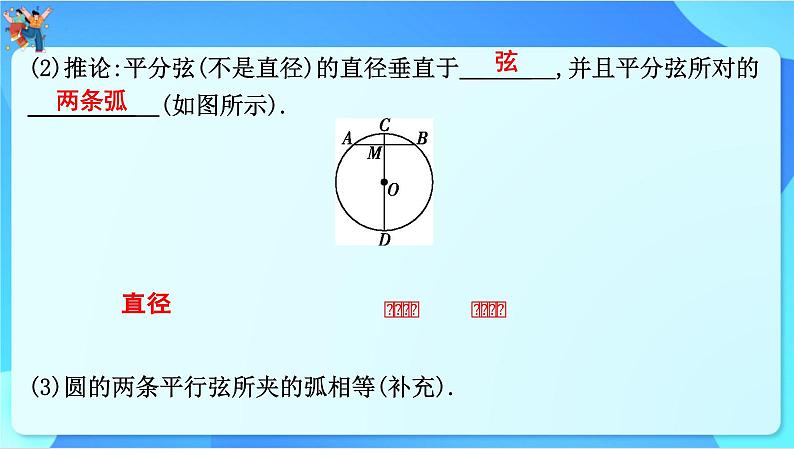
(2)推论:平分弦(不是直径)的直径垂直于　 　,并且平分弦所对的　 　(如图所示). 
(3)圆的两条平行弦所夹的弧相等(补充).
半径、弦心距和弦的一半构成直角三角形,满足勾股定理,常用于在圆中求线段的长.
3.弧、弦、弦心距、圆心角之间的关系(1)定理:在同圆或等圆中,相等的圆心角所对的弧　 　,所对的弦　 　,所对的弦的弦心距　 　. (2)推论:在同圆或等圆中,如果两个圆的圆心角、两条弧、两条弦或两条弦的弦心距中有一组量　 　,那么它们所对应的其余各组量都分别　 　. 4.圆周角定理及其推论(1)定理:一条弧所对的圆周角等于它所对的圆心角的　 　; (2)推论1:同弧或等弧所对的圆周角　 　; (3)推论2:半圆(或直径)所对的圆周角是　 　,90°的圆周角所对的弦是　 　. 
注意(1)在运用圆周角定理时,一定要注意“在同圆或等圆中”这个条件;(2)一条弦对着两条弧,对着无数个圆周角;(3)一条弧只对着一个圆心角,却对着无数个圆周角.5.圆内接四边形(1)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.(2)圆内接四边形的对角　 　. 
[典例1] (2022自贡)一块圆形玻璃镜面碎成了几块,其中一块如图所 示,测得弦AB长20 cm,弓形高CD为2 cm,则镜面半径为　 　cm. 
令镜面所在圆O的半径OB=r,则OC=r-2,根据勾股定理得OC2+BC2=OB2,进而求出半径.
在圆中,已知半径、弦、弦心距、弓形高中的两个量可以求出另外两个量;常过圆心作垂直于弦的直径,构造直角三角形,利用勾股定理和垂径定理或借助方程求解.
[变式1] (2022泸州)如图所示,AB是☉O的直径,OD垂直于弦AC于点D,DO的延长线交☉O于点E.若AC=4,DE=4,则BC的长是(　 　)
(1)两条等弧同时加上一段弧后两弧仍然相等,再通过等弧所对的弦相等即可证明;
求证:(1)AC=BD;(2)△ABE∽△DCE.
(2)根据同弧所对的圆周角相等,对顶角相等即可证明相似.
(2)∵∠B=∠C,∠AEB=∠DEC,∴△ABE∽△DCE.
应用弧、弦、圆心角的关系时的注意事项(1)必须有条件“在同圆或等圆中”;(2)可用来证明角相等、弧相等和弦相等.
圆周角定理及其推论(常考点)
连接AC,根据∠ABC=90°得出AC是圆形镜面的直径,再根据勾股定理求出AC即可得半径.
[变式2] (2023云南)如图所示,AB是☉O的直径,C是☉O上一点.若∠BOC=66°,则∠A等于(　 　)A.66°B.33°C.24°D.30°
[典例4] (2022宜昌)如图所示,四边形ABCD内接于☉O,连接OB,OD,BD,若∠C=110°,则∠OBD等于(　 　)A.15°B.20°C.25°D.30°
2.(2022长春)如图所示,四边形ABCD是☉O的内接四边形,若∠BCD=121°,则∠BOD的度数为(　 　)A.138°B.121°C.118°D.112°
3.(2023山西)如图所示,四边形ABCD内接于☉O,AC,BD为对角线,BD经过圆心O.若∠BAC=40°,则∠DBC的度数为(　 　)A.40°B.50°C.60°D.70°
4.(2023广元)如图所示,AB是☉O的直径,点C,D在☉O上,连接CD,OD,AC,若∠BOD=124°,则∠ACD的度数是(　 　)A.56°B.33°C.28°D.23°
5.(2023广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图所示,主桥拱呈圆弧形,跨度约为37 m,拱高约为 7 m,则赵州桥主桥拱半径约为(　 　)A.20 mB.28 mC.35 mD.40 m
(2022荆州)如图所示,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB= 20 cm,底面直径BC=12 cm,球的最高点到瓶底面的距离为32 cm,则球的半径为　 　cm.(玻璃瓶厚度忽略不计)