

湖北省利川市民族实验中学教联体2023-2024学年七年级下学期期中数学试题(含解析)
展开1.在下列实数中:0,,,,,,无理数有( )
A.1个B.2个C.3个D.4个
2.下列说法中正确的( ).
A.2022的相反数表示为B.9的算术平方根表示为
C.的绝对值表示为D.16的立方根表示为
3.如图所示,点在的延长线上,下列条件中能判断的是( )
A.B.
C.D.
4.下列不是假命题的有( )个
①两点之间,线段最短;②经过一点有且只有一条直线与已知直线平行;③内错角相等; ④直线外一点到这条直线的垂线段,叫做点到直线的距离.
A.1B.2C.3D.4
5.的大小关系为( )
A.B.
C.D.
6.在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为,点的对应点为,则点的坐标为( )
A.B.C.D.
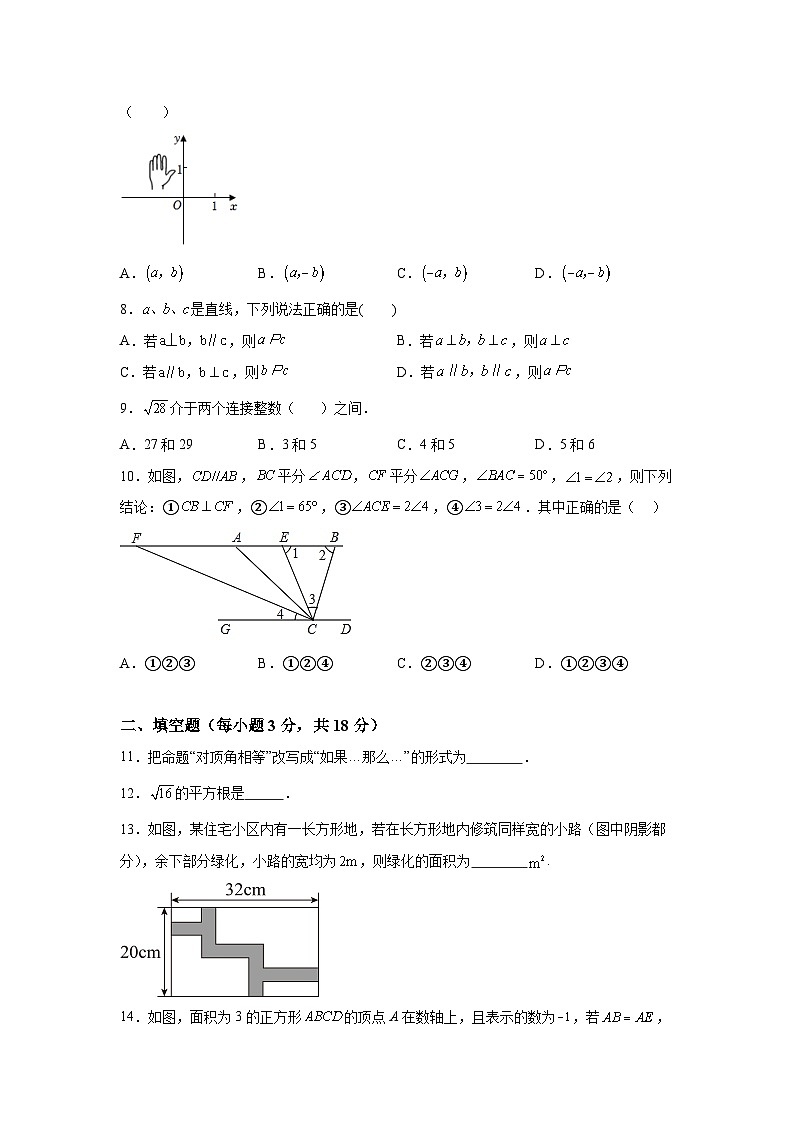
7.已知,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A.B.C.D.
8.是直线,下列说法正确的是( )
A.若,则B.若,则
C.若,则D.若,则
9.介于两个连接整数( )之间.
A.27和29B.3和5C.4和5D.5和6
10.如图,,平分,平分,,,则下列结论:①,②,③,④.其中正确的是( )
A.①②③B.①②④C.②③④D.①②③④
二、填空题(每小题3分,共18分)
11.把命题“对顶角相等”改写成“如果…那么…”的形式为 .
12.的平方根是 .
13.如图,某住宅小区内有一长方形地,若在长方形地内修筑同样宽的小路(图中阴影都分),余下部分绿化,小路的宽均为,则绿化的面积为 .
14.如图,面积为3的正方形的顶点A在数轴上,且表示的数为,若,则数轴上点E所表示的数为 .
15.在平面直角坐标系中,点 在第二象限,且距离轴个单位长度,距离轴 个单位长度,则点 的坐标为 .
16.如图,在平面直角坐标系xOy中,已知点A(2,1)、B(﹣1,1)、C(﹣1,﹣3)、D(2,﹣3),把一根长为2020个单位长度没有弹性的细线的一端固定在D处,并按D→C→B→A→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标为 .
三、解答题(共72分)
17.计算:
(1)
(2)
18.求x的值
(1)
(2)
19. 实数a,b,c是数轴上三点A,B,C所对应的数,如图,
(1)比较大小 a 0; 0; 0 ; 0
(2)化简:
20.如图,直线分别与直线,交于点E,F.平分,平分,且.求证:.
请在下面的证明过程中的横线处填写正确的结论或理由.
证明:(已知),
( ),
平分,(已知),
(角平分线定义),
又平分(已知),
(角平分线定义),
(等量代换),
( ).
21.已知:的立方根是的算术平方根是3,是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
22.如图,点A、B、C都落在网格的顶点上.
(1)写出点A、B、C的坐标;
(2)求△ABC的面积;
(3)把△ABC先向右平移4个单位长度,再向下平移5个单位长度,得△A´B´C´,画出△A´B´C´
23.如图,四边形ABCD中,,,分别是,的平分线
(1)与有什么关系,为什么?
(2)与有什么位置关系?请说明理由.
24.直线.
(1)如图1,当点为、内部一点时,连接、,请直接写出的度数;
(2)如图2,当点在直线上时,点在上,将线段沿方向平移得到线段,点在上,求证:;
(3)在(2)的条件下,如图3,点为线段上一点,在的延长线上取点,连接、,若平分,平分,,时,求的度数.
参考答案与解析
1.B
【分析】本题主要考查了无理数的定义以及算术平方根,解题的关键是掌握无限不循环小数是无理数,常见的无理数有:开不尽方的数,含的数,有规律但是不循环的数.
先将能化简的数化简,再根据无理数的定义逐个进行判断即可.
【解答】解:∵,
∴无理数有:,,共2个,
故选:B.
2.B
【分析】利用绝对值、相反数、算术平方根、立方根的表示方法进行判断即可.
【解答】解:A. 2022的相反数表示为-2022,故错误;
B. 9的算术平方根表示为,正确;
C. 的绝对值表示为,故错误;
D. 16的立方根表示为,故错误.
故选:B.
【点拨】本题主要考查的是绝对值、相反数、算术平方根、立方根的表示方法,掌握其基础性质是解题的关键.
3.B
【分析】本题主要考查平行线的判定,根据平行线的判定定理即可直接作出判断.
【解答】解:A、当时,不能证明,故该选项不符合题意;
B、当时,由内错角相等,两直线平行得,故该选项符合题意;
C、当时,得到,不能证明,故该选项不符合题意;
D、当时,由同旁内角互补,两直线平行能得到,不能证明,故该选项不符合题意.
故选:B.
4.A
【分析】本题考查判断命题的真假.根据线段的性质,平行公理,平行线的性质,点到直线的距离逐项分析判断,即可求解.
【解答】①两点之间,线段最短,不是假命题,符合题意;
②经过直线外一点有且只有一条直线与已知直线平行,原命题是假命题,不合题意;
③两直线平行,内错角相等,原命题是假命题,不合题意;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,原命题是假命题,不合题意.
故选:A.
5.B
【分析】先对题目中的无理数进行估算,再根据近似值的大小即可比较.
【解答】
解:,,,
而,
故选:B.
【点拨】本题考查的是同学们对无理数大小的估算能力及比较实数大小的方法,比较简单.
6.B
【分析】直接利用平移中点的变化规律求解即可.
【解答】横坐标从到,说明是向右移动了=,纵坐标从到,说明是向上移动了=,求原来点的坐标,则为让新坐标的横坐标都减,纵坐标都减.则点的坐标为.
【点拨】熟知点的平移规则是解题的关键.
7.B
【分析】本题考查了象限内点的坐标特征,不等式等知识点,因为,所以同号,又,所以,观察图形判断出小手盖住的点在第二象限,然后解答即可,记住各象限内点的坐标的符号是解题的关键.
【解答】∵,,
∴,
A、在第三象限,因为小手盖住的点在第二象限,故此选项不符合题意;
B、在第二象限,因为小手盖住的点在第二象限,故此选项符合题意;
C、在第四象限,因为小手盖住的点在第二象限,故此选项不符合题意;
D、在第一象限,因为小手盖住的点在第二象限,故此选项不符合题意;
故选:B.
8.D
【分析】本题考查了平行公理,根据平行公理以及平行线的性质判断即可.
【解答】解:A、在同一平面内,若,则,原说法错误,不符合题意;
B、在同一平面内,若,则,原说法错误,不符合题意;
C、在同一平面内,若,则,原说法错误,不符合题意;
D、若,则,正确,符合题意.
故选:D
9.D
【分析】由<< 可得<< 从而可得答案.
【解答】解:<<
<<
故选:
【点拨】本题考查的是无理数的估算,掌握无理数的估算的方法是解题的关键.
10.B
【分析】根据角平分线的性质可得,,再利用平角定义可得∠BCF=90°,进而可得①正确;首先计算出∠ACB的度数,再利用平行线的性质可得∠2的度数,从而可得∠1的度数;利用三角形内角和计算出∠3的度数,然后计算出∠ACE的度数,可分析出③错误;根据∠3和∠4的度数可得④正确.
【解答】解:如图,
∵BC平分∠ACD,CF平分∠ACG,
∴
∵∠ACG+∠ACD=180°,
∴∠ACF+∠ACB=90°,
∴CB⊥CF,故①正确,
∵CD∥AB,∠BAC=50°,
∴∠ACG=50°,
∴∠ACF=∠4=25°,
∴∠ACB=90°-25°=65°,
∴∠BCD=65°,
∵CD∥AB,
∴∠2=∠BCD=65°,
∵∠1=∠2,
∴∠1=65°,故②正确;
∵∠BCD=65°,
∴∠ACB=65°,
∵∠1=∠2=65°,
∴∠3=50°,
∴∠ACE=15°,
∴③∠ACE=2∠4错误;
∵∠4=25°,∠3=50°,
∴∠3=2∠4,故④正确,
故选:B.
【点拨】此题主要考查了平行线的性质,以及角平分线的性质,关键是理清图中角之间的和差关系.
11.如果两个角是对顶角,那么这两个角相等
【分析】本题考查了命题的概念,命题是由题设和结论两部分组成,根据命题的概念作答即可.
【解答】把命题“对顶角相等”改写成“如果…那么…”的形式为:
如果两个角是对顶角,那么这两个角相等.
故答案为:如果两个角是对顶角,那么这两个角相等.
12.±2
【解答】解:∵
∴的平方根是±2.
故答案为±2.
13.540
【分析】根据平移的性质将绿化部分转化为长为30m,宽为的长方形面积即可.
【解答】由平移可得到图
其中绿化部分的长为,宽为,
所以面积为,
故答案为:.
【点拨】本题考查平移,掌握平移的性质是正确解答的前提.
14.##
【分析】本题考查了实数与数轴,算术平方根的求解,先求出的长,再求出点E的坐标即可.
【解答】正方形的面积为3,
.
.
的坐标为,E在点A的右侧,
的坐标为.
故答案为:.
15.
【分析】根据点所在的象限,确定横纵坐标的符号,根据到轴、轴的距离,确定横纵坐标的数值,本题考查了点的坐标,解题的关键是:掌握四个象限内点的坐标符号特点,和到轴、轴的距离所对应的坐标数值.
【解答】解:点 在第二象限,
横坐标为负,纵坐标为正,
距离轴个单位长度,距离轴 个单位长度,
横坐标:,纵坐标为,
,
故答案为:.
16.(-1,-2)
【分析】由题意得绕四边形ABCD一周的细线长度为14,,即细线另一端在绕四边形第145圈的第4个单位长度的位置,即可得.
【解答】解:∵点A(2,1)、B(﹣1,1)、C(﹣1,﹣3)、D(2,﹣3),
∴,
,
,
,
∴绕四边形ABCD一周的细线长度为:,
,
∴细线另一端在绕四边形第145圈的第4个单位长度的位置,
即从点D向作沿,第4个单位所在的点的坐标即为所求,也就是点(-1,-2),
故答案为:(-1,-2).
【点拨】本题考查了点坐标规律,解题的关键是找出规律.
17.(1)
(2)
【分析】(1)先根据算术平方根及立方根的意义逐项化简,再算加减即可;
(2)先根据绝对值性质去绝对值及乘方、立方根的性质计算,再算加减即可.
【解答】(1)解:
;
(2)解:
.
【点拨】本题考查了实数的运算,正确化简各数是解答本题的关键.
18.(1)
(2)或
【分析】本题主要考查了求平方根的方法解方程,求立方根的方法解方程:
(1)根据求立方根的方法解方程即可;
(2)根据求平方根的方法解方程即可.
【解答】(1)解:∵,
∴,
∴;
(2)解:∵,
∴,
∴或.
19.(1)
(2)
【分析】本题主要考查了实数与数轴,实数的性质:
(1)根据数轴可得,据此可得答案;
(2)根据(1)所求先计算算术平方根,立方根和绝对值,再合并同类项即可得到答案.
【解答】(1)解:由数轴可知,,
∴,;
故答案为:;
(2)解:∵,,
∴
.
20.两直线平行,内错角相等;;;内错角相等,两直线平行
【分析】本题考查了平行线的判定与性质,熟记“两直线平行,内错角相等”及“内错角相等,两直线平行”是解题的关键.根据平行线的性质以及角平分线的定义,即可得到,进而得出结论.
【解答】证明:(已知),
(两直线平行,内错角相等),
平分,(已知),
(角平分线定义),
又平分(已知),
(角平分线定义),
(等量代换),
(内错角相等,两直线平行).
故答案为:两直线平行,内错角相等;;;内错角相等,两直线平行.
21.(1),,
(2)
【分析】本题考查了平方根、算术平方根、立方根的定义,无理数的估算.
(1)由立方根的定义可求得a的值,由算术平方根的定义可求得b的值,根据无理数的估算可确定c的值;
(2)把a、b、c的值代入代数式中求得代数式的值,即可求得其平方根;
【解答】(1)解:∵的立方根是,
∴,
解得,,
∵的算术平方根是3,
∴,
解得,,
∵,
∴,
∴的整数部分为6,
即,
因此,,,;
(2)解:当,,时,
,
∴.
22.(1)A(-1,4)、B(-4,3)、C(-3,1);(2);(3)见解析
【分析】(1)根据坐标系直接写出点的坐标即可;
(2)根据网格的特征用长方形的面积减去三个拐角三角形的面积即可;
(3)把A,B,C分别平移连接即可;
【解答】(1)根据平面直角坐标系得:A(-1,4)、B(-4,3)、C(-3,1);
(2);
(3)将A,B,C先向右平移4个单位长度,再向下平移5个单位长度,得到,,,连接即可,如图:
【点拨】本题主要考查了坐标与图形变化和平移的性质,准确分析计算是解题的关键.
23.(1),理由见解析
(2),理由见解析
【分析】(1)由角平分线的定义得,,根据四边形的内角和可得,进而可求出结论;
(2)由互余的性质可得,根据平行线的判定即可得出.
【解答】(1),理由:
∵,分别是,的平分线
∴,
∵
∴
∴
∴;
(2),理由:
在中,∵,
∴,
∵,
∴,
∴.
【点拨】本题考查了平行线的判定,多边形的内角和,直角三角形两锐角互余,关键是掌握四边形内角和为、同位角相等,两直线平行.
24.(1)
(2)见解析
(3)
【分析】(1)过点E作,证明,得出,,即可得出答案;
(2)根据平移的性质得出,根据平行线的性质得出,,即可证明结论;
(3)根据平行线的性质,结合角平分线的定义证明,过点作,得出,根据得出,根据平分,得出, 得出,即可求出答案.
【解答】(1)解:过点E作,如图所示:
∵,
∴,
∴,,
∴;
(2)证明:∵是由线段平移得到的,
∴,
∴,
∵,
∴,
∴.
(3)解:∵平分,
∴,
∵,
∴,,
∴,
过点作,如图所示:
∴,,
∴,
∵,
∴,
∴,
∵平分,
∴,
∴,
∴.
【点拨】本题主要考查了平行线的性质,角平分线的定义,平移的性质,平行公理的应用,解题的关键是熟练掌握平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
湖北省知名中小学教联体联盟2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份湖北省知名中小学教联体联盟2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含湖北省知名中小学教联体联盟2023-2024学年七年级下学期期中数学试题原卷版docx、湖北省知名中小学教联体联盟2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
湖北省恩施州利川市五校教联体2022-2023学年七年级下学期期中数学试题(解析版): 这是一份湖北省恩施州利川市五校教联体2022-2023学年七年级下学期期中数学试题(解析版),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湖北省黄冈市武穴市第二实验中学教联体2023-2024学年七年级上学期月考数学试题: 这是一份湖北省黄冈市武穴市第二实验中学教联体2023-2024学年七年级上学期月考数学试题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












