福建省福州第三中学2023-2024学年高一下学期4月期中数学试题（原卷版+解析版）

这是一份福建省福州第三中学2023-2024学年高一下学期4月期中数学试题（原卷版+解析版），文件包含福建省福州第三中学2023-2024学年高一下学期4月期中数学试题原卷版docx、福建省福州第三中学2023-2024学年高一下学期4月期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

审卷人：高一数学集备组
注意事项：
1．答题前，考生务必将自己的班级、准考证号、姓名填写在答题卡上．
2．第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷必须用0.5毫米黑色签字笔书写作答．若在试题卷上作答，答案无效．
第Ⅰ卷
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 下列向量关系式中，正确的是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】由向量加减法的运算规则，验证各选项的结果.
【详解】，A选项错误；
，B选项错误；
，C选项错误；
由向量加法的运算法则，有，D选项正确.
故选：D.
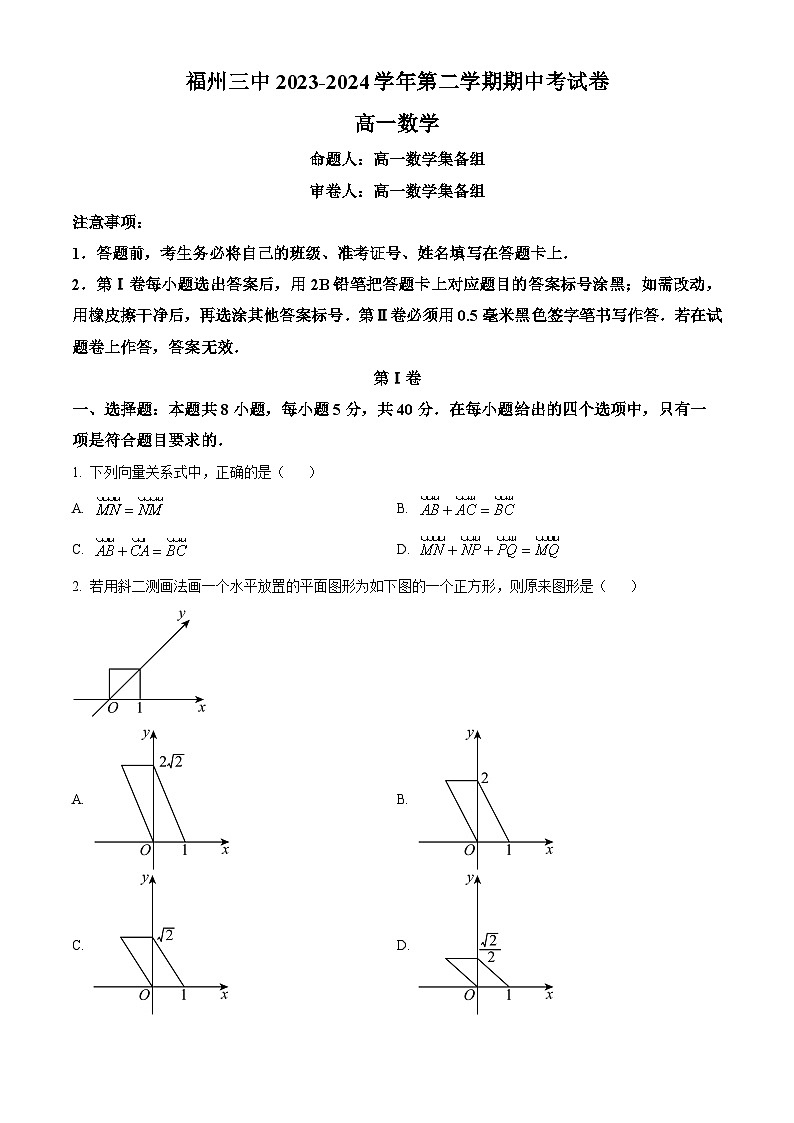
2. 若用斜二测画法画一个水平放置的平面图形为如下图的一个正方形，则原来图形是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】利用斜二测画法判断.
【详解】解：由斜二测画法知：平行或与x轴重合的线段长度不变，平行关系不变，
平行或与y轴重合的线段长度减半，平行关系不变，
故选：A
3. 若是两条不同的直线，垂直于平面，则“”是“”的
A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件
【答案】B
【解析】
【详解】若，因为垂直于平面，则或；若，又垂直于平面，则，所以“ ”是“ 的必要不充分条件，故选B．
考点：空间直线和平面、直线和直线的位置关系．
4. 设非零向量，满足，，则向量在方向上的投影向量（ ）
A. B. C. D.
【答案】A
【解析】
【分析】设的夹角为，求出即得解.
【详解】解：设的夹角为，
由得.
所以向量在方向上的投影向量为.
故选：A
5. 在正四棱台中， ，则该四棱台的体积为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】作出轴截面，过点作，结合等腰梯形的性质得高，再计算体积即可.
【详解】解：作出轴截面如图所示，过点作，垂足为，
因为正四棱台中，
所以，，，即梯形为等腰梯形，
所以，，
所以，该四棱台的体积为
故选：B
6. 如图，点为正方形的中心，平面，，是线段的中点，则（ ）
A. ，且直线是相交直线B. ，且直线是相交直线
C. ，且直线是异面直线D. ，且直线是异面直线
【答案】A
【解析】
【分析】连接，利用正方形中心的性质易得N为中点，所以易证明四点共面，再利用已知的空间关系就可以得证相等关系.
【详解】如图所示：连接，点为正方形的中心，
则经过点，且点为中点，又因为是线段的中点，
所以在中，，所以四点共面，即直线是相交直线；
因为平面，平面，所以，
又因为，所以，
又在正方形中可得：，所以，
同理可证，所以是正三角形，即，
故选：A．
7. 已知是所在平面内的一点，若|，则一定为（ ）
A. 以为底边的等腰三角形
B. 为底边的等腰三角形
C. 以为斜边的直角三角形
D. 以为斜边的直角三角形
【答案】C
【解析】
【分析】根据向量的线性运算，先得到，再由向量数量积的运算，化简整理，即可得出结果.
【详解】由得，
则，
所以，则，
所以，则，
所以是以为斜边的直角三角形.
故选：C.
8. 已知等边三角形的边长为4，D为的中点，将沿折到，使得为等边三角形，则直线与所成的角的余弦值（ ）
A. B. C. D.
【答案】D
【解析】
【分析】先根据异面直线夹角的定义找到直线与所成的角为，再利用余弦定理运算求解即可.
【详解】分别取，，的中点E，F，G，连接，，，，
则，，且，，，
所以直线与所成的角为（或其补角），
由题意可知：，，，，平面，
所以平面，
且平面，可得，则，
在中，由余弦定理可得，
所以直线与所成的角的余弦值为．
故选：D．
二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．
9. 已知m，n为两条不同的直线，，为两个不同的平面，则下列命题错误的是（ ）
A. 若，，，则B. 若，，，则
C. 若，，则D. 若，，则
【答案】ACD
【解析】
【分析】利用直线与平面的判定与性质定理及面面平行的定义、判定定理，结合空间直线、平面的位置关系逐项判断即可.
【详解】对于A，若，，，则或m与n相交或是异面直线，A错误；
对于B，由，得在平面内存在不同于n的直线l，使得，
由，得在平面内存在不同于n的直线，使得，于是，
而，则，又，因此，，B正确；
对于C，若，，则或与相交，C错误；
对于D，若，，则或，D错误.
故选：ACD
10. 已知内角A，B，C所对的边分别为a，b，c，则下列说法正确的是（ ）
A. 若，则
B. 若，，且该三角形有两解，则
C. 若，则为等腰三角形
D. 若，则为锐角三角形
【答案】ABD
【解析】
【分析】根据大边对大角及正弦定理判断A，根据图形数形结合可判断B，由正弦定理及三角恒等变换判断C，由两角和的正切公式变形可判断D.
【详解】因为，所以，由正弦定理，可知，故A正确；
如图，

，，且该三角形有两解，所以，即，
故B正确；
由正弦定理可得，，即，所以，因为，所以或，
即或，所以三角形为等腰或直角三角形，故C错误；
因为
，且，
所以，即为锐角，所以为锐角三角形，故D正确.
故选：ABD
11. 在棱长为2的正方体中，动点在正方形内运动（含边界），则（ ）
A. 有且仅有一个点，使得
B. 有且仅有一个点，使得平面
C. 当时，三棱锥的体积为定值
D. 有且仅有两个点，使得
【答案】BC
【解析】
【分析】结合图形根据约束条件由点的位置，逐一对个选项进行求解即可.
【详解】对于选项A，当与重合或与重合时满足，故A不正确；
对于选项B，因为A，，，平面，
所以平面，
若平面，则平面与平面重合，
此时必与重合，有且仅有一个点，使得平面，故B正确；
对于选项C，因为，平面，平面，所以面，
所以点到平面的距离等于到平面的距离，
所以为定值，故C正确；
对选项D，易知，，由，，得，
所以点的轨迹是侧面内以B为圆心，5为半径的弧，
即有无数个点满足题意，故D不正确．
故选：BC
第Ⅱ卷
三、填空题：本大题共3小题，每小题5分，共15分．
12. 已知轴截面为正三角形的圆锥的高与球O的直径相等，则圆锥的表面积与球O的表面积的比值是______．
【答案】1
【解析】
【分析】利用轴截面为等边三角形去写出圆锥底面半径，高，母线长之间的关系，再结合圆锥的高与球的直径相等，找到不同几何体之间的变量关系，再应用对应几何体的表面积公式即可解得.
【详解】设圆锥的底面半径为r，球O的半径为R，
因为圆锥的轴截面为正三角形，所以圆锥的高，母线，
由题可知：，所以球O的半径
所以圆锥的表面积，球O的表面积，
即，
故答案为：1．
13. 小明同学在广场上对纪念碑的高度进行测量，并绘制出测量方案示意图（如图），纪念碑的最顶端记为A点，纪念碑的最底端记为B点（B在A的正下方），在广场内（与B在同一水平面内）选取C，D两点，测得CD的长为15米，，在点C测得A的仰角为，在点D测得A的仰角为．根据以上测量数据，纪念碑的高度为______米．
【答案】15
【解析】
【分析】根据锐角三角函数的定义结合余弦定理即可求解.
【详解】设米，在中，，，得，
在中，，，得，
在中，，，则由余弦定理得，
，解得，即
所以纪念碑高度为15米．
故答案为：15．
14. 已知中，，，是线段上的两点，满足，，，，则__________．
【答案】
【解析】
【分析】根据角分线的向量性质及中线的向量性质化简得解.
【详解】由已知，
，则，
所以，则，
所以，
即，
即，
又点在上，所以，
所以，即，
又，
则，，
即，
联立，得，
解得，或（舍），
所以，则，
所以，
故答案为：.
四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．
15. 如图，在中，，点是的中点，设，

（1）用表示；
（2）如果，有什么位置关系？用向量方法证明你的结论.
【答案】（1），
（2），证明见解析
【解析】
【分析】（1）根据向量的线性运算法则，准确化简，即可求解；
（2）因为，化简，即可得到结论.
【小问1详解】
解：因为，所以，
因为是的中点，
可得
【小问2详解】
解：.
因，
则
以，所以.
16. 已知的内角A，B，C的对边分别为a，b，c，且．
（1）求B；
（2）若，的面积为，求．
【答案】（1）
（2）
【解析】
【分析】（1）利用正弦定理边化角，结合两角和的正弦公式化简，可得，即可求得答案；
（2）利用三角形面积公式求出，再由余弦定理求出答案
【小问1详解】
因为，所以，
即，
所以．
因为，所以，所以，
又，所以．
【小问2详解】
因为，所以
又由余弦定理得
即，解得.
17. 如图，在三棱柱中，D在线段AC上．
（1）若DAC中点，求证：平面；
（2）若M为BC的中点，直线平面，求．
【答案】（1）证明见解析
（2）2
【解析】
【分析】（1）连接交于点O，连接OD，证明，证明平面；
（2）设交于点E，连接DE，得到，利用平行即可求解.
【小问1详解】
连接交于点O，连接OD，
∵三棱柱，∴四边形为平行四边形，∴O为的中点，
又∵D为AC的中点，∴
∴平面，平面，∴平面
【小问2详解】
设交于点E，连接DE,
∵平面，平面，平面平面
∴，∴
又∵四边形为平行四边形，M为BC的中点
∴，∴
18. 在中，角A，B，C的对边分别为a，b，c，已知S为的面积且.
（1）若，求外接圆的半径；
（2）若为锐角三角形，求的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）利用三角形面积公式和余弦定理化简可得，计算可求，进而利用正弦定理求得外接圆的半径；
（2）由，设,由题意可求，利用正切函数的性质可求,可得,利用正弦定理，三角函数恒等变换的应用可求，,进而可求的取值范围.
【小问1详解】
∵S为的面积且，,
∴,即，,∴.
∴，解得：.
【小问2详解】
由（1）可知，，
∴
∵为锐角三角形，，∴，∴，∴，
设，则，
∴时，
19. 如图，在四棱锥中，平面，，，，，，E是的中点．
（1）证明：平面；
（2）若直线与平面所成的角和与平面所成的角相等，求四棱锥的体积．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）连接，证明，由线面垂直的性质证明，由线面垂直的判定定理即可得证；
（2）思路一：由线面角相等得，由等面积法求得，再求得底面梯形面积即可求解，思路二：由线面角相等得，由等体积法得，结合梯形面积公式、棱锥体积公式即可得解.
【小问1详解】
连接AC，
由，，，∴．
∵，E是中点，所以．
∵平面，平面，∴．
又∵，平面，∴平面．
【小问2详解】
过点B作交于G，交于F，
则由（1）可得平面，
∴平面．
∴为直线与平面所成的角，
又∵平面，∴为直线与平面所成的角．
又∵在和中，，是公共边，
∴，∴．
又∵，，∴四边形是平行四边形，
∴．∴．
在中，，，∴，
∴由得，即，
又∵梯形的面积为，
∴四棱锥的体积为；
第（2）问解法二：
因为平面，所以是在平面内的射影，
∠PBA是与平面所成的角，
设，则．
设B到平面的距离为d，与平面所成的角为，
则，
因为与平面所成的角与与平面所成的角相等，所以．
如图，在梯形中，
过C作于H，则，，所以，
由可得，所以．
过E作于F，则．
由，得，
即，所以，解得．
又∵梯形的面积为，
∴四棱锥的体积为．
20. 对于向量集，记向量．如果存在向量，使得，那么称是向量集的“长向量”．
（1）设向量，．若是向量集的“长向量”，求实数x的取值范围；
（2）设向量，，则向量集是否存在“长向量”？给出你的结论并说明理由；
（3）已知均是向量集的“长向量”，其中，．设在平面直角坐标系xOy中的点集，其中，，且与关于点对称，与关于点对称，求的最小值．
【答案】（1）
（2）存在“长向量”，且“长向量”为，，理由见解析
（3）4044
【解析】
【分析】（1）根据向量模长的不等关系，解得的范围即可；
（2）根据“长向量”的定义，结合三角函数的性质解不等式即可；
（3）根据向量坐标代入计算，结合向量不等式得到，再设，得到向量关系，从而求得最值.
【小问1详解】
由题意可得：，，，
则，解得：.
【小问2详解】
存在“长向量”，且“长向量”，，理由如下：
由题意可得，若存在“长向量”，只需使，
因为，，，，，，
所以，故只需使
，
即，即，
当或6时，符合要求，故存在“长向量”，且“长向量”为，.
【小问3详解】
由题意，得，，即，
即，同理，
三式相加并化简，得：，
即，，所以，
设，由，解得，
即
设，则依题意得：，
得，
故，
，
所以，
因为
所以，
当且仅当时等号成立，
所以.
【点睛】关键点点睛：本题考查向量新定义问题.关键点是根据已学知识，理解题中“长向量”的定义，将向量坐标代入计算，再结合向量不等式得到，得到向量关系，从而求得最值.