湖南省张家界市慈利县2023-2024学年八年级下学期期中考试数学试题

这是一份湖南省张家界市慈利县2023-2024学年八年级下学期期中考试数学试题，共10页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。
考生注意：全卷共有三道大题，满分100分，时量120分钟。
一、单选题（每小题3分，共10道小题，合计30分）
1．下列各组数中，以它们为边长能构成直角三角形的是（ ）
A．1，3，4B．2，3，4C．1，1，D．5，12，13
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A． B． C． D．
3．矩形具有而平行四边形不一定具有的性质是（ ）
A．对边相等B．对角相等
C．对角线相等D．对角线互相平分
4．直角三角形中，两直角边分别是和，则斜边上的中线长是（ ）
A．6.5B．C．D．
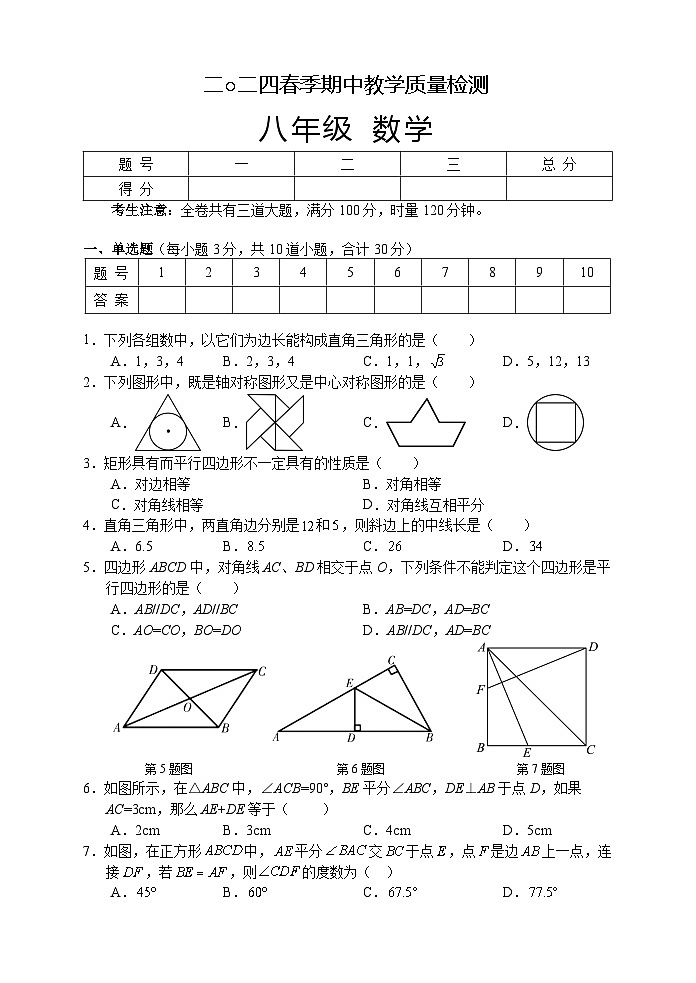
5．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）
A．AB//DC，AD//BCB．AB=DC，AD=BC
C．AO=CO，BO=DOD．AB//DC，AD=BC

第5题图 第6题图 第7题图
6．如图所示，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（ ）
A．2cmB．3cmC．4cmD．5cm
7．如图，在正方形中，平分交于点，点是边上一点，连接，若，则的度数为（ ）
A．B．C．D．
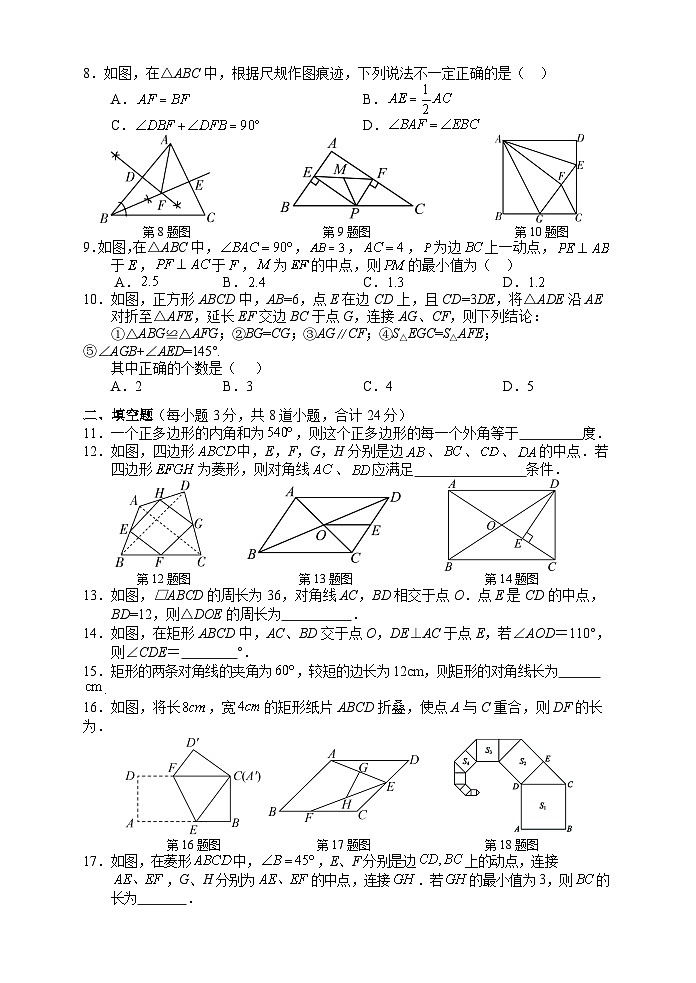
8．如图，在△ABC中，根据尺规作图痕迹，下列说法不一定正确的是（ ）
A．B．
C．D．

第8题图 第9题图 第10题图
9．如图，在△ABC中，，，，为边上一动点，于，于，为的中点，则的最小值为（ ）
A．B．C．D．
10．如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，则下列结论：
①△ABG≌△AFG；②BG=CG；③AG∥CF；④S△EGC=S△AFE；⑤∠AGB+∠AED=145°.
其中正确的个数是（ ）
A．2B．3C．4D．5
二、填空题（每小题3分，共8道小题，合计24分）
11．一个正多边形的内角和为，则这个正多边形的每一个外角等于 度．
12．如图，四边形中，E，F，G，H分别是边、、、的中点．若四边形为菱形，则对角线、应满足 条件．

第12题图 第13题图 第14题图
13．如图，□ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ．
14．如图，在矩形ABCD中，AC、BD交于点O，DE⊥AC于点E，若∠AOD＝110°，则∠CDE＝ °．
15．矩形的两条对角线的夹角为，较短的边长为12cm，则矩形的对角线长为 .
16．如图，将长，宽的矩形纸片ABCD折叠，使点A与C重合，则DF的长为．

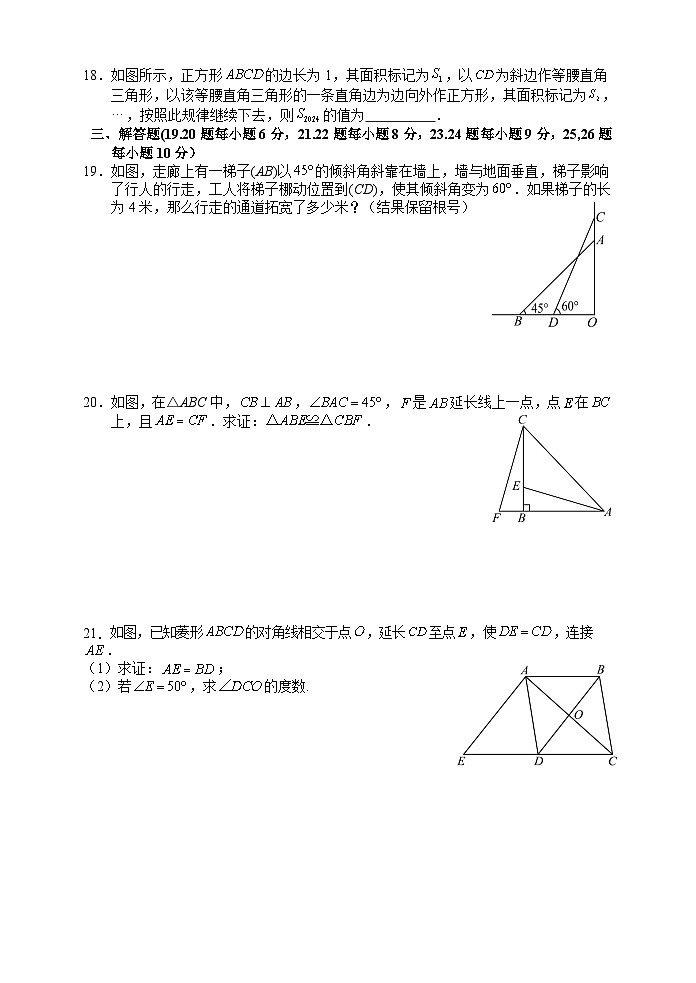
第16题图 第17题图 第18题图
17．如图，在菱形中，，E、F分别是边上的动点，连接，G、H分别为的中点，连接．若的最小值为3，则的长为 ．
18．如图所示，正方形的边长为1，其面积标记为，以为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为，，按照此规律继续下去，则的值为 ．
三、解答题(19.20题每小题6分，21.22题每小题8分，23.24题每小题9分，25,26题每小题10分）
19．如图，走廊上有一梯子(AB)以的倾斜角斜靠在墙上，墙与地面垂直，梯子影响了行人的行走，工人将梯子梛动位置到(CD)，使其倾斜角变为．如果梯子的长为4米，那么行走的通道拓宽了多少米？（结果保留根号）
20．如图，在△ABC中，，，是延长线上一点，点在上，且．求证：．
如图，已知菱形的对角线相交于点，延长至点，使，连接．
（1）求证：；
（2）若，求的度数.
22．如图，已知矩形，延长至点，使得，对角线，交于点，连结．
（1）求证：四边形是平行四边形；
（2）若，，求的长．
23．如图，在△ABC中，，是边上的中线，E是的中点，过点A作的平行线交的延长线于点F，连接．
（1）求证：四边形是菱形；
（2）若，平行线与间的距离为，求菱形的面积．
24．如图，在菱形中，对角线，交于点O，过点A作的垂线，垂足为点E，延长到点F，使，连接．
（1）求证：四边形是矩形；
（2）连接，若，，求的长．
25．在△ABC中，，D为△ABC内一点，连接，，延长到点，使得
（1）如图1，延长到点，使得，连接，，若，求证：；
（2）连接，交的延长线于点，连接，依题意补全图2，若，用等式表示线段与的数量关系，并证明．

26．如图，以点A为旋转中心将正方形逆时针旋转角，得到正方形．作直线，过点F作，垂足为H，连接．
（1）如图1，当时，请直接写出和的数量关系；
（2）如图2，当时，（1）中的结论是否成立，如果成立请证明，如果不成立请说明理由；
（3）当点E在的垂直平分线上时，请直接写出的长度.
题 号
一
二
三
总 分
得 分
题 号
1
2
3
4
5
6
7
8
9
10
答 案
二○二四年春季期中教学质量检测
八年级数学参考答案
一、选择题（每小题3分，共10道小题，合计30分）
11．7212．13．1514．35
15．2416．317．18．
19．行走的通道拓宽了米
解：∵，，
∴，，
∴，分
∵，
∴，
∴分
则．
答：行走的通道拓宽了米．分
20．证明略。（6分）
21．（1）四边形是菱形，
，，，，
四边形是平行四边形，
；分
（2）由（1）可知，四边形是平行四边形，
，，
四边形是菱形，
，
，
．分
22．解：（1）四边形是矩形，
，．，
，．
四边形是平行四边形．分
（2）解：过点作于点．
矩形，，
是的中点，
是的中位线，有．分
在中，，，
．分
23．（1）∵是的中点，
∴．∵，
∴，，
在和中，∴，∴．
∵是边中线，，
∴，∴．
∵，∴四边形是平行四边形．
∵，∴四边形是菱形．分
（2）作于点G，则，
∵，
∴是等边三角形，，
∴，
∵，
∴，∴，
∴，
∴菱形的面积是．（4分）
24．（1）证明：四边形是菱形，
且，，
，，
，
四边形是平行四边形， 分
，，
四边形是矩形；分
（2）解：四边形是菱形，
，，
，，
，
，，
．分
25．（1）证明：在和中，
，∴ ，∴ ，
∴ ，
∵，∴． 分
（2）解：补全后的图形如图所示，，分
证明如下：
延长BC到点M，使CM＝CB，连接EM，AM，
∵，CM＝CB，
∴ 垂直平分BM，∴，
在和中，，
∴ ，
∴ ，，
∵，∴ ，∴ ，
∵，∴，
∴，即，
∵，∴ ，∴ ．分
26．（1） （2）成立，见解析 （3）或
（1）解：
理由：∵正方形逆时针旋转得到正方形，
∴，，，
∴，都是等边三角形，
∴，，
∴，
又，∴，∴；分
（2）解：（1）中结论成立，
理由：过A作于M，
由（1）知：，
∴，
∵，，，
∴，
∴，
∵，，
∴，，
∴，
∵， ，
∴∴，∴；分
（3）解：①当点E在下方时，
如图，过点E作于N，
∵点E在的垂直平分线上，
∴，
∴，∴，
∴，
由（2）知：；分
②当点E在上方时，
如图，过点E作延长线于N，
同理：，，∴，
∴，
由（2）知：；
综上，的长度为或．分1
2
3
4
5
6
7
8
9
10
D
D
C
A
D
B
C
B
D
C