2023-2024学年山东省青岛市即墨区多校联考七年级（下）期中数学试卷（含解析）

这是一份2023-2024学年山东省青岛市即墨区多校联考七年级（下）期中数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.计算(−54)2023×(−0.8)2024=( )
A. −1B. 1C. −1.25D. −0.8
2.新时代中国科技事业蓬勃发展，清华大学团队首次制备出亚1纳米栅极长度的晶体管，实现等效的物理栅长为0.34纳米，将数据0.00000000034米用科学记数法表示为( )
A. 3.4×10−9B. 0.34×10−9C. 3.4×10−10D. 0.34×10−10
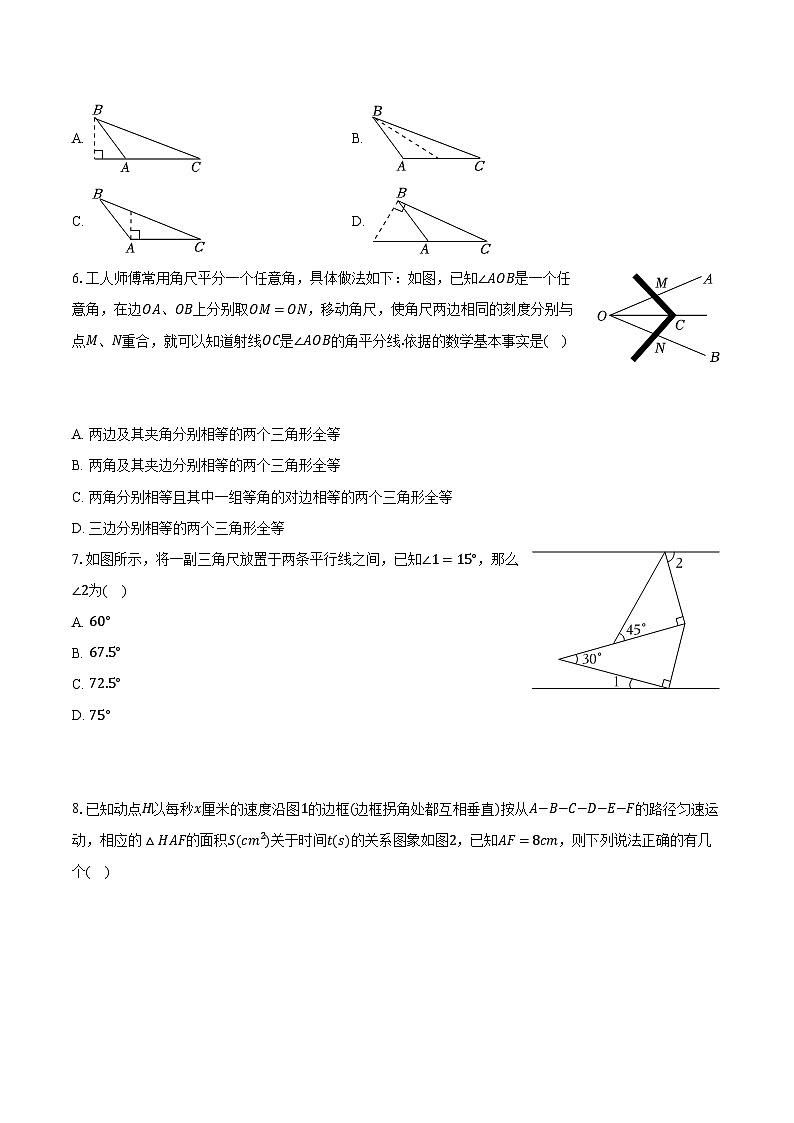
3.如图，将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分)，并将剩余部分沿虚线剪开，得到两个长方形，再将这两个长方形拼成一个大的长方形.这两个图能解释一个等式是( )
A. x(x−1)=x2−xB. (x−1)(x+1)=x2−1
C. (x−1)2=x2−2x+1D. (x+1)2=x2+2x+1
4.下列说法中正确的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 两条直线有两种位置关系：平行或相交
C. 同一平面内，垂直于同一直线的两条直线平行
D. 三条线段两两相交，一定有三个交点
5.下列各图中，正确画出AC边上的高线的是( )
A. B.
C. D.
6.工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M、N重合，就可以知道射线OC是∠AOB的角平分线.依据的数学基本事实是( )
A. 两边及其夹角分别相等的两个三角形全等
B. 两角及其夹边分别相等的两个三角形全等
C. 两角分别相等且其中一组等角的对边相等的两个三角形全等
D. 三边分别相等的两个三角形全等
7.如图所示，将一副三角尺放置于两条平行线之间，已知∠1=15°，那么∠2为( )
A. 60°
B. 67.5°
C. 72.5°
D. 75°
8.已知动点H以每秒x厘米的速度沿图1的边框(边框拐角处都互相垂直)按从A−B−C−D−E−F的路径匀速运动，相应的△HAF的面积S(cm2)关于时间t(s)的关系图象如图2，已知AF=8cm，则下列说法正确的有几个( )
①动点H的速度是2cm/s；
②BC的长度为3cm；
③当点H到达D点时△HAF的面积是8cm2；
④b的值为14；
⑤在运动过程中，当△HAF的面积是30cm2时，点H的运动时间是3.75s和10.25s．
A. 2个B. 3个C. 4个D. 5个
二、填空题：本题共8小题，每小题3分，共24分。
9.小明在进行两个多项式的乘法运算时，不小心把一个多项式乘以(x−2y)错抄成除以(x−2y)，结果得到(3x−y)，则该多项式是______．
10.有一条长方形纸带，按如图方式折叠，图中的∠1=130°，则∠2的度数为______．
11.如图，在2×2的正方形网格中，线段AB、CD的端点均在格点上，则∠1+∠2=______°.
12.若3x+y−4=0，则8x⋅2y的结果是______．
13.某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
设鸭的质量为x千克，烤制时间为t，估计当x=6千克时，t的值为______分．
14.现有若干张卡片，分别是正方形卡片A、B和长方形卡片C，卡片大小如图所示，如果要拼一个长为(a+2b)，宽为(a+b)的大长方形，则需要C类卡片张数为______张.
15.小亮在计算3m(11m+4n)的值时，把n的值看错了，其结果等于25，细心的小敏把正确的n的值代入计算，其结果也是25.为了探究明白，她又把n=2023代入，结果还是25.则m的值为______．
16.我们知道下面的结论：若am=an(a>0,a≠1)，则m=n.利用这个结论解决下列问题：设2m=3，2n=6，2p=12.现给出关于m，n，p之间的关系式：①n−m=1；②m+p=2n；③m+n=2p−3；④n+p=4m.其中正确的有______.(填序号)
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题4分)
如图，已知∠α，用尺规作图作∠β，使∠β=2∠α，不写作法，但要保留作图痕迹．
18.(本小题12分)
计算：
(1)(−3a2)3+2a2⋅a4−a8÷a2；
(2)(π−3.14)0−(12)−3−12022；
(3)(2a+b)(b−2a)−(a−3b)2；
(4)(x+y−3)(x−y+3)．
19.(本小题6分)
先化简，再求值：(x−3)2+(x+4)(x−4)+2x(2−x)，其中x=−2．
20.(本小题8分)
一汽车油箱里有油40L，在行驶过程中，每小时耗油2.5L，回答下列问题：
(1)汽车行驶1h后油箱里还有油______L，汽车行驶6h后油箱里还有油______L；
(2)这一变化过程中共有______个变量，其中______是变量，______是常量；
(3)设汽车行驶的时间为x h，油箱里剩下的油为Q L，请用含x的式子表示Q；
(4)这辆汽车最多能行驶多少小时？
21.(本小题8分)
小明从家出发骑自行车去上学，当他以往常的速度骑了一段路后，突然想起要买圆规，于是又折回到刚经过的文具店，买到圆规后继续骑车去学校.如图是他本次上学过程中离家距离与所用时间的关系图，根据图象回答下列问题：
(1)小明家到学校的路程是______米；
(2)小明在文具店停留了______分钟；
(3)本次上学途中，小明一共行驶了______米；
(4)交通安全不容忽视，我们认为骑自行车的速度超过15千米/时就超过了安全限度.通过计算说明：在整个上学途中哪个时间段小明的骑车速度最快，最快速度在安全限度内吗？
22.(本小题6分)
如图，已知三点B、C、D在同一条直线上，∠B=∠1，∠2=∠E，试说明AC/​/ED的理由．
解：因为∠B=∠1，(已知)
所以AB//CE.(______)
所以∠2= ______.(______)
因为∠2=∠E，(已知)
所以______=∠E.(______)
所以AC//ED.(______)
23.(本小题8分)
如图，点B、E在AF上，已知△ABC≌△FED，∠A和∠F是对应角，CB和DE是对应边．
(1)再写出其他的一组对应边和一组对应角；
(2)判断AC与DF的位置关系，并说明理由；
(3)若AF=8，BE=2，求AB的长．
24.(本小题8分)
知识储备：我们知道，把完全平方公式(a±b)2=a2±2ab+b2适当变形，可解决很多数学问题.例如：若a+b=3，ab=1，则a2+b2的值为______．
获得新知：若(5−m)(m−4)=−3，求(5−m)2+(m−4)2的值．
解：设a=5−m，b=m−4，则ab=−3，a+b=1，
∴a2+b2=(a+b)2−2ab=1−2×(−3)=7，即(5−m)2+(m−4)2=7．
解决问题：
(1)若x满足(30−x)2+(x−20)2=120，求(30−x)(x−20)的值；
(2)如图，一户人家有一块长方形土地ABCD，AB=30，AD=24，其内部有一条宽度为a的L型种植区域①，其余部分(长方形AEFG)为种植区域②，测量区域②的面积为340；阿凡提有两块正方形的土地AGHI与AJKE跟这户人家的种植区域②相邻，正方形土地的边长分别为AG与AE.这户人家对阿凡提的两块地垂涎已久，提出要将自己的土地与阿凡提交换，阿凡提有没有损失呢？请你运用所学的数学知识进行解释．
25.(本小题12分)
(1)方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在△ABC中，AB=8，AC=6，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法(如图2)，
①延长AD到M，使得DM=AD；
②连接BM，通过三角形全等把AB、AC、2AD转化在△ABM中；
③利用三角形的三边关系可得AM的取值范围为AB−BM方法总结：上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系．
(2)请你写出图2中AC与BM的数量关系和位置关系，并加以证明．
(3)深入思考：如图3，AD是△ABC的中线，AB=AE，AC=AF，∠BAE=∠CAF=90°，请直接利用(2)的结论，试判断线段AD与EF的数量关系，并加以证明．
答案和解析
1.【答案】D
【解析】解：原式=(−54)2023×(45)2023×45
=(−54×45)2023×45
=−45
=−0.8．
故选：D．
根据幂的乘方与积的乘方法则进行解题即可．
本题考查幂的乘方与积的乘方，熟练掌握运算法则是解题的关键．
2.【答案】C
【解析】解：将0.00000000034用科学记数法表示应为3.4×10−10．
故选：C．
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
本题考查了用科学记数法表示较小的数，掌握形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定是关键．
3.【答案】B
【解析】解：将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分)，剩余部分的面积为两个正方形的面积差，即x2−1，
将剩余部分沿着虚线剪开，拼成的长方形的长为(x+1)，宽为(x−1)，因此面积为(x+1)(x−1)，
所以有x2−1=(x+1)(x−1)，
即(x+1)(x−1)=x2−1，
故选：B．
用“两种”方法分别用代数式表示裁剪后剩余部分的面积和拼成的长方形的面积即可．
本题考查平方差公式的几何背景，掌握平方差公式的结构特征是正确解答的关键．
4.【答案】C
【解析】解：A、根据平行公理：经过直线外一点，有且只有一条直线与已知直线平行，可判断A不合题意；
B、两条不重合的直线有两种位置关系：平行和相交，可判断B不符合题意；
C、同一平面内，垂直于同一直线的两条直线平行，可判断C符合题意；
D、三条线段两两相交，有三个交点或一个交点，可判断D不合题意．
故选：C．
根据“经过直线外一点，有且只有一条直线与已知直线平行”和两条直线的位置关系判断A、B；根据平行线的判定定理和相交线段的交点问题判断C、D选项的正误．
本题主要考查了相交线，平行线的判定和两直线的位置关系，熟练掌握定义和公理是解题的关键．
5.【答案】A
【解析】解：△ABC中AC边上的高即为过点B作AC的垂线段，该垂线段即为AC边上的高，四个选项中只有选项D符合题意，
故选：A．
根据三角形高的定义判断即可得到答案．
本题主要考查了三角形高线定义，解题的关键是熟知过三角形一个顶点作对边的垂线得到的线段叫三角形的高．
6.【答案】D
【解析】解：∵角尺两边相同的刻度分别与点M、N重合
∴CM=CN，
在△OCM和△OCN中，
CM=CNOM=ONOC=OC，
∴△OCM≌△OCN(SSS)，
∴∠MOC=∠NOC，
即OC平分∠AOB，
∴依据的数学基本事实是三边分别相等的两个三角形全等．
故选：D．
依题意得CM=CN，然后可依据“SSS”判定△OCM和△OCN全等，从而得∠MOC=∠NOC，据此可得出所依据的数学基本事实．
此题主要考查了全等三角形的判定，熟练掌握三边分别相等的两个三角形全等是解决问题的关键．
7.【答案】D
【解析】解：如下图所示，作∠3，∠4，∠5，
∠5=180°−∠1−90°=75°，
∵∠4=∠5，
∴∠4=75°，
∵∠3=180°−90°−60°，
∴∠3=30°，
∴∠2=180°−∠3−∠4=180°−30°−75°=75°，
故选：D．
先求出∠3和∠4的度数，再根据三角形内角和定理求解即可．
本题考查了三角形内角和定理和平行直线的性质，熟记三角形内角和定理是解题的关键．
8.【答案】A
【解析】解：当点H在AB上时，如图所示，
AH=xt (cm)，
S△HAF=12×AF×AH=4xt(cm2)，
此时三角形面积随着时间增大而逐渐增大，
当点H在BC上时，如图所示，HP是△HAF的高，且HP=AB，
∴S△HAF=12×AF×AB，此时三角形面积不变，
当点H在CD上时，如图所示，HP是△HAF的高，C，D，P三点共线，
S△HAF=12×AF×HP，点H从点C点D运动，HP逐渐减小，故三角形面积不断减小，
当点H在DE上时，如图所示，HP是△HAF的高，且HP=EF，
S△HAF=12×AF×EF，此时三角形面积不变，
当点H在EF时，如图所示，
S△HAF=12×AF×HF，点H从点E向点F运动，HF逐渐减小，故三角形面积不断减小直至零，
对照图2可得0≤t≤5时，点H在AB上，
S△HAF=4xt=4⋅5x=40(cm2)，
∴x=2，AB=2×5=10(cm)，
∴动点H的速度是2cm/s，
故①正确，
5≤t≤8时，点H在BC上，此时三角形面积不变，
∴动点H由点B运动到点C共用时8−5=3(s)，
∴BC=2×3=6(cm)，
故②错误，
8≤t≤12时，当点H在CD上，三角形面积逐渐减小，
∴动点H由点C运动到点D共用时12−8=4(s)，
∴CD=2×4=8(cm)，
∴EF=AB−CD=10−8=2(cm)，
在D点时，△HAF的高与EF相等，即HP=EF，
∴S△HAF=12×AF×EF=12×8×2=8(cm2)，
故③正确，
12≤t≤b，点H在DE上，DE=AF−BC=8−6=2(cm)，
∴动点H由点D运动到点E共用时2÷2=1(s)，
∴b=12+1=13，
故④错误．
当△HAF的面积是30cm2时，点H在AB上或CD上，
点H在AB上时，S△HAF=4xt=8t=30(cm2)，
解得t=3.75(s)，
点H在CD上时，
S△HAF=12×AF×HP=12×8×HP=30(cm2)，
解得HP=7.5(cm)，
∴CH=AB−HP=10−7.5=2.5(cm)，
∴从点C运动到点H共用时2.5÷2=1.25(s)，
由点A到点C共用时8s，
∴此时共用时8+1.25=9.25(s)，
故⑤错误．
故选：A．
先根据点H的运动，得出当点H在不同边上时△HAF的面积变化，并对应图2得出相关边的边长，最后经过计算判断各个说法．
本题是动点函数的图象问题．考查了三角形的面积公式，函数图象的性质，理解函数图象上的点表示的意义，是解决本题的关键．
9.【答案】3x2−7xy+2y2
【解析】解：由题意可知该多项式为：(3x−y)⋅(x−2y)
=3x2−6xy−xy+2y2
=3x2−7xy+2y2
故答案为：3x2−7xy+2y2
根据整式的运算法则即可求出答案．
本题考查整式的运算，解题的关键是熟练整式的运算法则，本题属于基础题型．
10.【答案】25°
【解析】解：如图，
由折叠的性质可得∠3=180°−∠12=180°−130°2=25°，
由长方形纸带的对边平行得，∠2+∠3+∠1=180°，
∴∠2=180°−25°−130°=25°，
故答案为：25°．
由折叠的性质求出∠3的度数，由长方形纸带的对边平行求出∠2的度数即可．
本题考查了平行线的性质，折叠的性质，熟练掌握这两个知识点是解题的关键．
11.【答案】90
【解析】解：由题意可得CO=AO，BO=DO，
在△AOB和△COD中AO=CO∠O=∠OBO=DO，
∴△AOB≌△COD(SAS)，
∴∠1=∠BAO，
∵∠2+∠BAO=90°，
∴∠1+∠2=90°．
故答案为：90．
首先证明△AOB≌△COD，利用全等三角形的性质可得∠1=∠BAO，进而可得答案．
此题主要考查了全等三角形的判定及性质，关键是掌握全等图形的判定方法和性质．
12.【答案】16
【解析】解：∵3x+y−4=0，
∴3x+y=4，
∴8x⋅2y=(23)x⋅2y=23x⋅2y=23x+y=24=16．
故答案为：16．
根据幂的乘方与积的乘方法则、同底数幂的乘法法则进行解题即可．
本题考查幂的乘方与积的乘方、同底数幂的乘法，熟练掌握运算法则是解题的关键．
13.【答案】260
【解析】解：由题意得，鸭的质量每增加1千克，烤制时间增加40分，
故该函数解析式为t=40x+20，
∴当x=6时，
t=40×6+20=260分，
故答案为：260．
由题意可得该函数解析式为t=40x+20，再将x=6代入求解即可．
此题考查了运用函数解决实际问题的能力，关键是能正确理解问题间数量关系，并正确运用函数知识进行求解．
14.【答案】3
【解析】解：(a+2b)(a+b)=a2+3ab+2b2．
则需要C类卡片张数为3张．
故答案为：3．
拼成的大长方形的面积是(a+2b)(a+b)=a2+3ab+2b2，即需要一个边长为a的正方形，2个边长为b的正方形和3个C类卡片的面积是3ab．
本题考查了多项式乘多项式的运算，需要熟练掌握运算法则并灵活运用，利用各个面积之和等于总的面积也比较关键．
15.【答案】±5
【解析】解：3m(11m+4n)
=25m2−4n2+9m2+12mn+4n2−33m2−12mn
=m2，
所以这个结果与n的取值无关，是25，
∵m2=25，
∴m=±5；
故答案为：±5．
先根据整式混合运算的法则化简原式，得出这个结果与n的取值无关，进一步即可求出m．
本题考查了整式的混合运算，正确理解题意、熟练掌握整式混合运算的法则是解题的关键．
16.【答案】①②③
【解析】解：∵2m=3，2n=6，
∴2n−m=2n÷2m=6÷3=2=21，
∴n−m=1，故①正确，符合题意；
∴2m+p=2m⋅2p=3×12=36=62=(2n)2=22n，
∵2p=12，
∴m+p=2n，故②正确，符合题意；
∵2m+n=2m⋅2n=3×6=18，22p−3=22p÷23=(2p)2÷8=122÷8=144÷8=18，
∴2m⋅2n=2m+n=22p−3，
∴m+n=2p−3，故③正确，符合题意；
∵2n+p=2n⋅2p=6×12=48，24m=(2m)4=34=81，
∴2n+p≠24m，
∴n+p≠4m，故④错误，不符合题意；
∴正确的有：①②③，
故答案为：①②③．
根据同底数幂的除法的逆运算法则可以判断①；根据同底数幂的乘法的逆运算法则及幂的乘方的逆运算法则可以判断②；根据同底数幂的乘法的逆运算法则、同底数幂的除法的逆运算法则及幂的乘方的逆运算法则可以判断③；根据同底数幂的乘法的逆运算法则及幂的乘方的逆运算法则可以判断可以判断④．
本题主要考查了同底数幂的除法的逆运算、同底数幂的乘法的逆运算及幂的乘方的逆运算，熟练掌握运算法则是解题的关键．
17.【答案】解：如图，∠AOB即为所求．

【解析】利用尺规根据要求作出图形即可．
本题考查作图−复杂作图，解题的关键是熟练掌握五种基本作图，属于中考常考题型．
18.【答案】解：(1)(−3a2)3+2a2⋅a4−a8÷a2
=−27a6+2a6−a6
=−26a6；
(2)(π−3.14)0−(12)−3−12022
=1−8−1
=−8；
(3)(2a+b)(b−2a)−(a−3b)2
=b2−4a2−(a2−6ab+9b2)
=b2−4a2−a2+6ab−9b2
=−8b2−5a2+6ab；
(4)(x+y−3)(x−y+3)
=[x+(y−3)][x−(y−3)]
=x2−(y−3)2
=x2−y2+6y−9．
【解析】(1)先算乘方，再算乘除，后算加减，即可解答；
(2)先化简各式，然后再进行计算即可解答；
(3)利用平方差公式，完全平方公式进行计算，即可解答；
(4)利用平方差公式，完全平方公式进行计算，即可解答．
本题考查了整式的混合运算，平方差公式，完全平方公式，零指数幂，负整数指数幂，准确熟练地进行计算是解题的关键．
19.【答案】解：(x−3)2+(x+4)(x−4)+2x(2−x)
=x2−6x+9+x2−16+4x−2x2
=−2x−7，
当x=−2时，原式=−2×(−2)−7=4−7=−3．
【解析】先利用完全平方公式，平方差公式，单项式乘多项式的法则进行计算，然后把x的值代入化简后的式子进行计算，即可解答．
本题考查了整式的混合运算−化简求值，完全平方公式，平方差公式，准确熟练地进行计算是解题的关键．
20.【答案】37.5 25 2 邮箱里剩下的油量和行驶的时间 每小时耗油的油量
【解析】解：(1)40−2.5=37.5(L)，
40−2.5×6=25(L)，
故答案为：37.5；25．
(2)这一变化过程中共有2个变量，
其中邮箱里剩下的油量和行驶的时间是变量，
每小时耗油的油量是常量，
故答案为：2；邮箱里剩下的油量和行驶的时间；每小时耗油的油量．
(3)Q=40−2.5x．
(4)40−2.5x=0，
解得x=16．
答：这辆汽车最多能行驶16小时．
(1)根据邮箱里剩下的油量=油箱里原有的油量−耗油的油量，即可求出答案．
(2)根据题中的三个数量：油箱里原有的油量、油箱里剩下的油量和行驶的时间，直接判断出变化的量就是变量和不变的量就是常量．
(3)根据邮箱里的剩下的油量=油箱里原有的油量−每小时耗油的油量×时间，直接用字母表达即可．
(4)根据题意，使剩下的油量Q=0，即可用表达式求出结果．
本题考查了常量和变量的问题，解题的关键是根据题中的等量关系式来解答．
21.【答案】1800 3 3000
【解析】解：(1)由图象可得，小明家到学校的路程是1800米，
故答案为：1800；
(2)小明在书店停留了12−9=3(分钟)，
故答案为：3；
(3)本次上学途中，小明一共行驶了：
1200+(1200−600)+(1800−600)=1200+600+1200=3000(米)，
故答案为：3000；
(4)当时间在0～6分钟内时，速度为：1200÷6=200(米/分)，
当时间在6～9分钟内时，速度为：(1200−600)÷(9−6)=200(米/分)，
当时间在12～15分钟内时，速度为：(1800−600)÷(15−12)=400(米/分)，
15千米/时=250米/分，
∵400>250，
∴在12～15分钟时间段小明的骑车速度最快，不在安全限度内．
(1)根据函数图象中的数据可以得到小明家到学校的路程和在书店停留的时间；
(2)根据函数图象中的数据可以得到小明在书店停留的时间；
(3)根据函数图象中的数据可以得到本次上学途中，小明一共行驶的路程；
(4)根据题意和函数图象可以得到各段内对应的速度，从而可以解答本题．
本题考查从函数的图象中获取信息，解题的关键是利用数形结合的思想解答．
22.【答案】同位角相等，两直线平行 ∠ACE 两直线平行，内错角相等 ∠ACE 等量代换 内错角相等，两直线平行
【解析】解：因为∠B=∠1(已知)
所以AB//CE(同位角相等，两直线平行)
所以∠2=∠ACE(两直线平行，内错角相等)
因为∠2=∠E(已知)
所以∠ACE=∠E(等量代换)
所以AC//ED(内错角相等，两直线平行)
故答案为：同位角相等，两直线平行；∠ACE；两直线平行，内错角相等；∠ACE；等量代换；内错角相等，两直线平行．
根据平行线的性质与判定进行填空，即可求解．
本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．
23.【答案】解：(1)∵△ABC≌△FED，
∴∠ABC和∠DEF是对应角，∠C和∠D是对应角，AC和FD是对应边，AB和EF是对应边；(答案不唯一)
(2)AC//DF．
理由：因为△ABC≌△FED，
所以∠A=∠F，
所以AC/​/DF．
(3)因为△ABC≌△FED，
所以AB=FE，
所以AB−BE=FE=BE，即AE=BF．
因为AF=8，BE=2，
所以AE+BF=AF−BE=6，
所以AE=3，
所以AB=AE+BE=5．
【解析】(1)根据全等三角形的性质求解即可；
(2)根据全等三角形的性质得到∠A=∠F，即可判定AC/​/DF；
(3)根据全等三角形的对应边相等得到AB=FE，进而得出AE=BF，根据线段的和差求解即可．
此题考查了全等三角形的性质，熟记全等三角形的性质是解题的关键．
24.【答案】7
【解析】解：知识储备：a2+b2=(a+b)2−2ab=32−2×1=7，
故答案为：7；
(1)2(30−x)(x−20)=[(30−x)+(x−20)]2−[(30−x)2+(x−20)2]=102−120=−20，
∴(30−x)(x−20)=−10；
(2)由题意得，AG=AD−DG=24−a，AE=AB=BE=30−a，(24−a)(30−a)=340，
长方形ABCD的面积=30×24=720，
正方形AGHI、正方形AJKE的面积=(24−a)2+(30−a)2=[(30−a)−(24−a)]2+2(30−a)(24−a)=62+2×340=716，
∵716<720，
∴阿凡提没有损失．
知识储备：a2+b2=(a+b)2−2ab可得；
(1)2(30−x)(x−20)=[(30−x)+(x−20)]2−[(30−x)2+(x−20)2]，代入(30−x)2+(x−20)2=120，可得；
(2)由题意得，AG=AD−DG=24−a，AE=AB=BE=30−a，(24−a)(30−a)=340，分别计算长方形ABCD的面积和正方形AGHI、正方形AJKE的面积，进行比较可得阿凡提有没有损失．
把他开除了整式的混合运算，关键是掌握完全平方公式．
25.【答案】解：(1)1(2)AC//BM，且AC=BM，
理由是：由(1)知，△MDB≌△ADC，
∴∠M=∠CAD，AC=BM，
∴AC//BM；
(3)EF=2AD，
理由：如图，延长AD到M，使得DM=AD，连接BM，
由(1)知，△BDM≌△CDA(SAS)，
∴BM=AC，
∵AC=AF，
∴BM=AF，
由(2)知：AC//BM，
∴∠BAC+∠ABM=180°，
∵∠BAE=∠FAC=90°，
∴∠BAC+∠EAF=180°，
∴∠ABM=∠EAF，
在△ABM和△EAF中，
AB=EA∠ABM=∠EAFBM=AF
∴△ABM≌△EAF(SAS)，
∴AM=EF，
∵AD=DM，
∴AM=2AD，
∵AM=EF，
∴EF=2AD，
即：EF=2AD．
【解析】【分析】
本题是三角形综合题，考查了全等三角形的判定和性质，倍长中线法，构造全等三角形是解本题的关键．
(1)先判断出BD=CD，由“SAS”可证△MDB≌△ADC，得出BQ=AC=6，最后用三角形三边关系即可得出结论；
(2)由(1)知，△MDB≌△ADC，根据全等三角形的性质和平行线的判定即可得出结论；
(3)同(1)的方法得出△BDM≌△CDA，则BM=AC，进而判断出∠ABM=∠EAF，进而判断出△ABM≌△EAF，得出AM=EF，∠BAM=∠AEF，即可得出结论．
【解答】
解：(1)如图2，延长AD到M，使得DM=AD，连接BM，
∵AD是△ABC的中线，
∴BD=CD，
在△MDB和△ADC中，
BD=CD∠BDM=∠CDADM=AD
∴△MDB≌△ADC(SAS)，
∴BM=AC=6，
在△ABM中，AB−BM∴8−6∴1故答案为：1(2)见答案；
(3)见答案．鸭的质量/千克
1
1.5
2
2.5
3
3.5
4
烤制时间/分
60
80
100
120
140
160
180