

2024年河北省石家庄市高考数学质检试卷(一)(含详细答案解析)
展开1.抛物线y2=−12x的准线方程是( )
A. y=12B. y=18C. x=14D. x=18
2.已知复数z1=21+i,复数z2=2i,则|z1−z2|=( )
A. 1B. 2C. 10D. 10
3.已知命题p:∀x∈(0,+∞),ex>lnx,则( )
A. p是假命题,¬p:∃x∈(−∞,0),ex≤lnx
B. p是假命题,¬p:∃x∈(0,+∞),ex≤lnx
C. p是真命题,¬p:∃x∈(−∞,0),ex≤lnx
D. p是真命题,¬p:∃x∈(0,+∞),ex≤lnx
4.已知圆台O1O上下底面圆的半径分别为1,3,母线长为4,则该圆台的侧面积为( )
A. 8πB. 16πC. 26πD. 32π
5.下列不等式成立的是( )
A. lg60.5>lg60.7B. 0.60.5>lg0.60.5
C. lg60.6>lg50.5D. 0.60.6>0.60.5
6.集校为了解本校高一男生身高和体重的相关关系,在该校高一年级随机抽取了7名男生,测量了他们的身高和体重得下表:
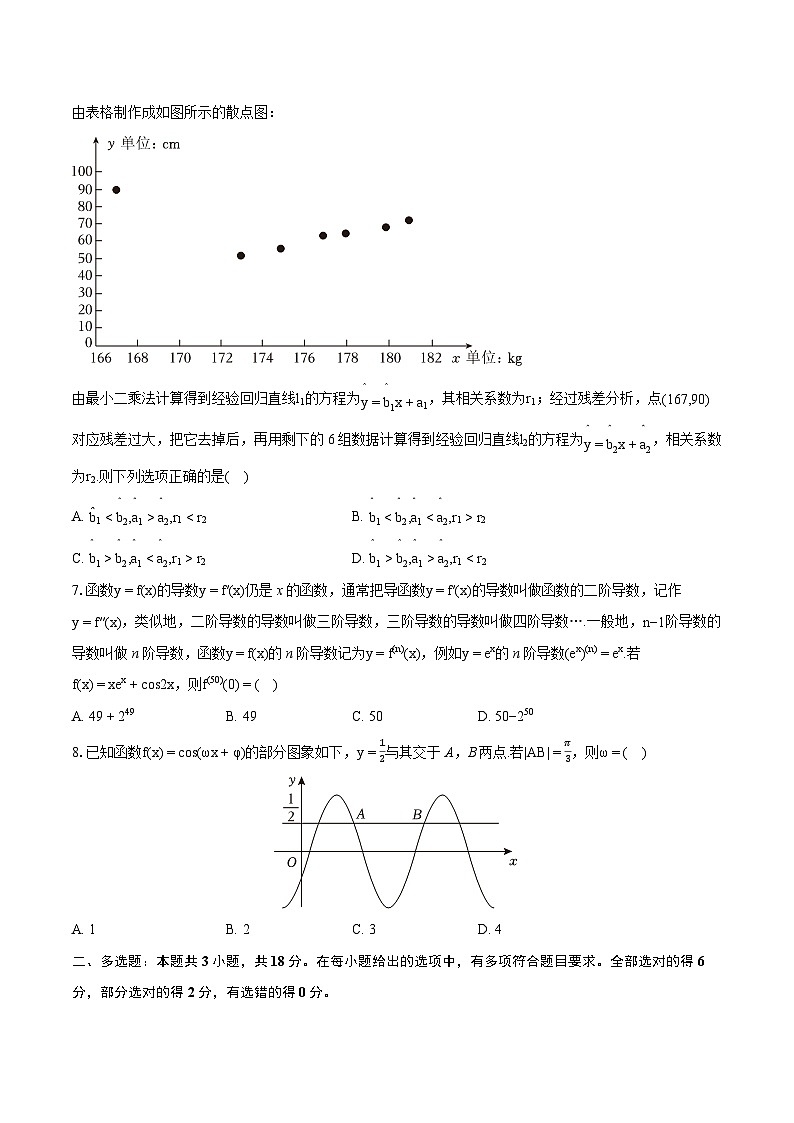
由表格制作成如图所示的散点图:
由最小二乘法计算得到经验回归直线l1的方程为y =b 1x+a1,其相关系数为r1;经过残差分析,点(167,90)对应残差过大,把它去掉后,再用剩下的6组数据计算得到经验回归直线l2的方程为y =b 2x+a 2,相关系数为r2.则下列选项正确的是( )
A. b1a 2,r1
C. b 1>b 2,a 1r2D. b 1>b 2,a 1>a 2,r1
A. 49+249B. 49C. 50D. 50−250
8.已知函数f(x)=cs(ωx+φ)的部分图象如下,y=12与其交于A,B两点.若|AB|=π3,则ω=( )
A. 1B. 2C. 3D. 4
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.甲在一次面试活动中,7位考官给他们打分分别为:61、83、84、87、90、91、92.则下列说法正确的有( )
A. 这7个分数的第70百分位数为87
B. 这7个分数的平均数小于中位数
C. 去掉一个最低分和一个最高分后,分数的方差会变小
D. 去掉一个最低分和一个最高分后,分数的平均数会变小
10.如图,在圆柱O1O中,轴截面ABCD为正方形,点F是AB的上一点,M为BD与轴O1O的交点,E为MB的中点,N为A在DF上的射影,且EF//平面AMN,则下列选项正确的有( )
A. CF//平面AMN
B. AN⊥平面DBF
C. DB⊥平面AMN
D. F是AB的中点
11.已知F1,F2是双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点,|F1F2|=2c,P(x1,y1)为C右支上一点,F1P⊥F2P,△F1PF2的内切圆的圆心为E(x2,y2),半径为r,直线PE与x轴交于点M(x3,0),则下列结论正确的有( )
A. x2=a
B. r= c2+a2−c
C. x1x3=x22
D. 若△F1PF2的内切圆与y轴相切,则双曲线C的离心率为 3+1
三、填空题:本题共3小题,共13分。
12.已知向量a,b的夹角为π6,且|a|=2,|b|=1,则|a+ 3b|=______.
13.已知x是第二象限角,若cs(x−70∘)=15,则sin(x+110∘)=______.
14.已知等差数列{an}的公差与等比数列{bn}的公比相等,且b1−a1=1,b2−a2=1,b3−a4=1,则bn=______;若数列{an}和{bn}的所有项合在一起,从小到大依次排列构成一个数列{cn},数列{cn}的前n项和为Sn,则使得Sncn+1>12成立的n的最小值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足a2+b2+ 2ab=c2.
(1)求角C的大小;
(2)若b=1,c=2bcsB,求△ABC的面积.
16.(本小题15分)
如图,P为圆锥的顶点,AC为圆锥底面的直径,△PAC为等边三角形,O是圆锥底面的圆心,△ABD为底面圆O的内接正三角形,且边长为2 3,点E为线段PC中点.
(1)求证:平面BED⊥平面ABD;
(2)M为底面圆O的劣弧AB上一点,且∠ACM=30∘.求平面AME与平面PAC夹角的余弦值.
17.(本小题15分)
已知椭圆E:x2a2+y2b2=1(a>b>0)过点(1,83),且其离心率为13.
(1)求椭圆E的方程;
(2)过点(−1,0)的斜率不为零的直线与椭圆E交于C,D两点,A,B分别为椭圆E的左、右顶点.直线AC,BD交于一点P,M为线段PB上一点,满足OM//PA.问OA⋅OM是否为定值.若是,求出该定值;若不是,说明理由(O为坐标原点).
18.(本小题17分)
某商场周年庆进行大型促销活动,为吸引消费者,特别推出“玩游戏,送礼券”的活动,活动期间在商场消费达到一定金额的人可以参加游戏,游戏规则如下:在一个盒子里放着六枚硬币,其中有三枚正常的硬币,一面印着字,一面印着花;另外三枚硬币是特制的,有两枚双面都印着字,一枚双面都印着花,规定印着字的面为正面,印着花的面为反面.游戏者蒙着眼睛随机从盒子中抽取一枚硬币并连续投掷两次,由工作人员告知投掷的结果,若两次投掷向上的面都是正面,则进入最终挑战,否则游戏结束,不获得任何礼券.最终挑战的方式是进行第三次投掷,有两个方案可供选择:方案一,继续投掷之前抽取的那枚硬币,如果掷出向上的面为正面,则获得200元礼券,方案二,不使用之前抽取的硬币,从盒子里剩余的五枚硬币中再次随机抽取一枚投掷,如果数出向上的面为正面,则获得300元礼券,不管选择方案一还是方案二,如果掷出向上的面为反面,则获得100元礼券.
(1)求第一次投掷后,向上的面为正面的概率.
(2)若已知某顾客抽取一枚硬币后连续两次投掷,向上的面均为正面,求该硬币是正常硬币的概率.
(3)在已知某顾客进入了最终挑战环节的条件下,试分别计算他选择两种抽奖方案最终获得的礼券的数学期望,并以此判断应该选择哪种抽奖方案更合适.
19.(本小题17分)
已知函数f(x)=ex−ax2,(a>0).
(1)若函数f(x)有3个不同的零点,求a的取值范围;
(2)已知f′(x)为函数f(x)的导函数,f′(x)在R上有极小值0,对于某点P(x0,f(x0)),f(x)在P点的切线方程为y=g(x),若对于∀x∈R,都有(x−x0)⋅[f(x)−g(x)]≥0,则称P为好点.
①求a的值;②求所有的好点.
答案和解析
1.【答案】D
【解析】【分析】
本题考查抛物线的性质,考查学生的计算能力,属于基础题.
抛物线y2=−12x的开口向左,且2p=12,由此可得抛物线y2=−12x的准线方程.
【解答】
解:抛物线y2=−12x的开口向左,且2p=12,∴p2=18
∴抛物线y2=−12x的准线方程是x=18
故选D.
2.【答案】C
【解析】解:∵z1=21+i=2(1−i)(1+i)(1−i)=1−i,
∴|z1−z2|=|1−i−2i|=|1−3i|= 1+9= 10.
故选:C.
化简复数z1,利用复数的运算和模长公式求解.
本题考查复数的模长公式,属于基础题.
3.【答案】D
【解析】解:∀x∈(0,+∞),ex的图象恒在y=lnx图象的上方,
则ex>lnx,p为真命题,
¬p:∃x∈(0,+∞),ex≤lnx,故D正确.
故选:D.
先判断命题的真假,再结合命题否定的定义,即可求解.
本题主要考查全称命题的否定,属于基础题.
4.【答案】B
【解析】解:圆台O1O上下底面圆的半径分别为1,3,母线长为4,
所以圆台的侧面积为S侧=π(r+r′)l=π(1+3)×4=16π.
故选:B.
根据圆台的侧面积公式计算即可.
本题考查了圆台的侧面积计算问题,是基础题.
5.【答案】C
【解析】解:对于A,∵y=lg6x是(0,+∞)上的增函数,且0.7>0.5,
∴lg60.5
∴0.60.5
∴lg60.6>lg50.6,
又∵y=lg5x是(0,+∞)上的增函数,且0.6>0.5,
∴lg50.6>lg50.5,
∴lg60.6>lg50.5,故C正确;
对于D,∵y=0.6x在R上单调递减,且0.6>0.5,
∴0.60.6<0.60.5,故D错误.
故选:C.
利用指数函数和对数函数的单调性求解.
本题主要考查了指数函数和对数函数的性质,属于基础题.
6.【答案】A
【解析】解:由散点图可知,身高与体重正相关,r1>0,r2>0,
因为离群点(167,90)的纵坐标90相对过大,
所以去掉离群点后回归直线的截距变小而斜率变大,所以a 2b 1,
去掉离群点后样本数据的信息相关程度更强,拟合效果会更好,
所以r1
由散点图可知r1>0,r2>0,去掉离群点后回归直线的截距变小、斜率变大,而拟合效果会更好,进而得到结果.
本题主要考查了散点图的应用,考查了线性回归方程的性质,属于中档题.
7.【答案】D
【解析】解:f′(x)=ex+xex−2sin2x=(x+1)ex−2sin2x,f′′(x)=ex+(x+1)ex−4cs2x=(x+2)ex−4cs2x,
∴f(50)(x)=(x+50)ex−250cs2x,
∴f(50)(0)=50−250.
故选:D.
可通过求一阶导数和二阶导数找规律,从而得出f(x)的50阶导数,然后即可得出答案.
本题考查了基本初等函数和复合函数的求导公式,是中档题.
8.【答案】D
【解析】解:设A(x1,12),B(x2,12),则由|AB|=π3,得x2−x1=π3,
由csx=12,得x=π3+2kπ或x=5π3+2kπ,k∈Z,
由图可知,ωx2+φ−(ωx1+φ)=5π3−π3=4π3,即ω(x2−x1)=4π3,
所以ω=4.
故选:D.
根据余弦函数的性质即可得.
本题考查三角函数的性质,属于中档题.
9.【答案】BC
【解析】解:选项A,7×70%=4.9,所以第70百分位数为90,故选项A错误.
选项B,中位数为87,平均数为(61+83+84+87+90+91+92)÷7=588÷7=84,
所以平均数小于中位数,故选项B正确;
选项C,去掉一个最低分和一个最高分后,分数更为集中,离散程度减小,所以方差会变小,故选项C正确;
选项D,平均数为(61+83+84+87+90+91+92)÷7=588÷7=84,
去掉一个最低分和一个最高分后,平均数为(83+84+87+90+91)÷5=435÷5=87,所以平均数会变大,故选项D错误.
故选:BC.
根据平均数、中位数、方差和百分位数的定义求解.
本题主要考查了平均数、中位数、方差和百分位数的定义,属于基础题.
10.【答案】BCD
【解析】解:对A选项,如图,延长AM,则AM过C,
∴CF与平面AMN交于点C,∴A选项错误;
对B选项,∵AB为圆O的直径,∴BF⊥AF,
又AD⊥底面圆O,且BF⊂底面圆O,∴BF⊥AD,
又AF∩AD=A,且AF,AD⊂平面ADF,
∴BF⊥平面ADF,又AN⊂平面ADF,
∴AN⊥BF,又AN⊥DF,BF∩DF=F,且BF,DF⊂平面DBF,
∴AN⊥平面DBF,∴B选项正确;
对C选项,由B选项分析可知:AN⊥平面DBF,又BD⊂平面DBF,
∴BD⊥AN,又轴截面ABCD为正方形,
∴BD⊥AM,又AN∩AM=A,且AN,AM⊂平面AMN,
∴BD⊥平面AMN,∴C选项正确;
对D选项,∵EF//平面AMN,
又EF⊂平面DEF,且平面AMN∩平面DEF=MN,
∴EF//MN,又易知DMME=2,
∴DNNF=DMME=2,
设NF=x,则DN=2x,DF=3x,设正方形截面ABCD的边长为2,
由AN⊥DF,可得AN2=AD2−DN2=4−4x2,
∴AF2=AN2+NF2=4−4x2+x2=4−3x2,又AD⊥AF,
∴AD2+AF2=DF2,
∴4+4−3x2=9x2,∴x2=23,
∴AF2=4−3x2=2,∴AF= 2,
又AB=2,BF⊥AF,∴BF= 2,∴AF=BF,
∴F是AB的中点,∴D选项正确.
故选:BCD.
根据线面平行的性质定理,线面垂直的判定定理,解三角形,即可分别求解.
本题考查线面平行的性质定理,线面垂直的判定定理,解三角形,属中档题.
11.【答案】ACD
【解析】解:A.如图,
作EF⊥PF2,EG⊥F1F2,EH⊥PF1,
根据切线长定理,|PH|=|PF|,|F1H|=|F1G|,|F2F|=|F2G|,
又|PF1|−|PF2|=2a,所以|F1H|−|FF2|=2a,|F1G|−|F2G|=2a,
所以(c+x2)−(c−x2)=2a,即x2=a,故A正确;
B.因为|PF1|−|PF2|=2a,PF1⊥PF2,
所以|PF2|2+(|PF2|+2a)2=4c2,解得:|PF2|= 2c2−a2−a,|PF1|= 2c2−a2+a,
所以r=2S△PF1F2C△PF1F2=|PF1||PF2||PF1|+|PF2|+|F1F2|=(2c2−a2)−a22 2c2−a2+2c=b2 c2+b2+c= c2+b2−c,故B错误;
C.由内切圆的性质可知,PE为角平分线,则|PF1||PF2|=|MF1||MF2|,即ex1+aex1−a=x3+cc−x3,整理为2ex1x3=2ac,即cax1x3=ac,
所以x1x3=a2,由A选项的证明可知,a2=x22,即x1x3=x22,故C正确;
D.若△F1PF2的内切圆与y轴相切,则r=x2,
则由选项AB知,a= c2+b2−c,即2c2−a2=(a+c)2,
则c2−2ac−2a2=0,即e2−2e−2=0,e= 3+1或e=1− 3(舍),
所以双曲线C的离心率为 3+1,故D正确.
故选:ACD.
利用切线性质,判断A,利用内切圆的半径表示三角形的面积,即可判断B,利用角平分线定理和焦半径公式,结合判断C,根据几何关系,转化为关于a,c的齐次方程,即可判断D.
本题主要考查双曲线的性质,属于中档题.
12.【答案】 13
【解析】解:由题意,向量a,b的夹角为π6,
且|a|=2,|b|=1,
所以|a+ 3b|= (a+ 3b)2
= a2+2 3a⋅b+3b2
= 4+2 3×2×1× 32+3
= 13.
故答案为: 13.
根据平面向量数量积的性质及题设条件进行运算即可.
本题考查平面向量数量积的性质及运算,属基础题.
13.【答案】−2 65
【解析】解:∵x∈(90∘,180∘),∴x−70∘∈(20∘,110∘),且cs(x−70∘)=15,
∴sin(x−70∘)=2 65,
∴sin(x+110∘)=sin(70∘−x)=−sin(x−70∘)=−2 65.
故答案为:−2 65.
根据三角函数的诱导公式和平方关系即可得解.
本题考查了诱导公式和平方关系的运用,是基础题.
14.【答案】2n 27
【解析】解:设等差数列{an}的公差d与等比数列{bn}的公比q相等,即d=q,q≠0,
由b1−a1=1,b2−a2=1,b3−a4=1,可得b1q−(a1+d)=1,b1q2−(a1+3d)=1,
解得d=q=2,a1=1,b1=2,
则bn=2n,an=2n−1;
设cn=2k,
则Sn=[(2×1−1)+(2×2−1)+(2×3−1)+…+(2×2k−1−1)]+(2+22+…+2k)
=2k−1(1+2⋅2k−1−1)2+2(1−2k)1−2=22k−2+2k+1−2.
由Sn>12cn+1得22k−2+2k+1−2>12(2k+1)⇒(2k−1)2−20⋅2k−1−14>0.
⇒2k−1≥25,∴k≥6.
所以只需研究25
cn+1=2m+1,m为等差数列的项数,且m>16.
由m2+26−2>12(2m+1)得m2−24m+50>0,
∴m≥22,n=m+5≥27.
故满足条件的n最小值为27.
故答案为:2n,27.
先根据等差数列以及等比数列的通项公式,解方程可得首项和公差、公比,可得所求bn;
再由等差数列和等比数列的求和公式确定满足条件的项数的取值范围,再列不等式求满足条件的项数的最小值.
本题考查分组求和方法、等差数列和等比数列的通项公式与求和公式,考查推理能力与计算能力,属于难题.
15.【答案】解:(1)因为a2+b2+ 2ab=c2,
所以由余弦定理可得csC=a2+b2−c22ab=− 2ab2ab=− 22,
又C∈(0,π),
所以C=3π4;
(2)因为b=1,c=2bcsB,C=3π4,
所以sinC=2sinBcsB=sin2B= 22,
又B∈(0,π4),可得2B∈(0,π2),
所以2B=π4,可得B=π8,
所以A=π−B−C=π−π8−3π4=π8=B,可得a=b=1,
所以△ABC的面积S=12absinC=12×1×1× 22= 24.
【解析】(1)由题意利用余弦定理可得csC的值,结合C∈(0,π),即可求解C的值;
(2)由题意利用正弦定理,二倍角公式可求sin2B= 22,可求2B∈(0,π2),可得B=π8,利用三角形内角和定理可求A=B,可得a=b=1,进而利用三角形的面积公式即可求解.
本题主要考查了正弦定理,余弦定理,二倍角公式,三角形内角和定理以及三角形的面积公式在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.
16.【答案】(1)证明:设AC,BD交于F,连接EF,
在△ABD中,由正弦定理知,AC=2R=BDsinA=4,
在△OFB中,OF=OBsin30∘=1,
所以F为OC中点,所以EF//PO,
又PO⊥平面ABD,所以EF⊥平面ABD,
又EF⊂平面BED,因此平面BED⊥平面ABD;
(2)解:由(1)知,FA,FB,FE两两垂直,
以点F为坐标原点,FA,FB,FE所在直线分别为x轴,y轴,z轴,
建立如图所示空间直角坐标系,
则A(3,0,0),M(2, 3,0),E(0,0, 3),
故AM=(−1, 3,0),AE=(−3,0, 3),
设平面AME的一个法向量为n1=(x,y,z),
则由n1⋅AM=−x+ 3y=0n1⋅AE=−3x+ 3z=0,令x= 3,可得y=1,z=3,
则平面AME的一个法向量为n1=( 3,1,3),
不妨取平面PAC的一个法向量为n2=(0,1,0),
则cs
因此平面AME与平面PAC夹角的余弦值为 1313.
【解析】(1)设AC,BD交于F,连接EF,证明EF//PO,则可得PO⊥平面ABD,由面面垂直的判定定理即可证得结论;
(2)建立空间直角坐标系,求得平面AME与平面PAC的法向量,利用向量夹角公式求得面面角的夹角余弦值.
本题考查面面垂直的判定,考查面面角夹角余弦值求法,属中档题.
17.【答案】解:(1)设椭圆的半焦距为c,
由题意知,1a2+649b2=1ca=13a2−b2=c2,解得a2=9,b2=8,
所以C的方程为x29+y28=1.
(2)设直线CD的方程为x=ty−1,C(x1,y1),D(x2,y2),
联立x=ty−1x29+y28=1,得(8t2+9)y2−16ty−64=0,
所以y1+y2=16t8t2+9,y1y2=−648t2+9,
由题意知,A(−3,0),B(3,0),
所以直线AC的方程为y=y1x1+3(x+3),直线BD的方程为y=y2x2−3(x−3),
联立两条直线的方程可得x=−3[x1y2+x2y1+3(y2−y1)]x2y1−x1y2−3(y1+y2)=−3[(ty1−1)y2+(ty2−1)y1+3(y2−y1)](ty2−1)y1−(ty1−1)y2−3(y1+y2)=−3×2ty1y2+2y2−4y1−4y1−2y2=6(ty1y2+y2−2y1)4y1+2y2,
即xP=6(ty1y2+y2−2y1)4y1+2y2,
因为OM//PA,且O是AB的中点,所以M是PB的中点,
所以xM=xP+32=3ty1y2+6y24y1+2y2,
所以OA⋅OM=(−3,0)⋅(3ty1y2+6y24y1+2y2,yM)=−3×3ty1y2+6y24y1+2y2=−9×ty1y2+2y24(y1+y2)−2y2=−9×t⋅−648t2+9+2y24⋅16t8t2+9−2y2=9,是定值.
【解析】(1)将点(1,83)代入椭圆方程,再结合椭圆的几何性质,解方程组求出a2和b2的值即可;
(2)设直线CD的方程为x=ty−1,将其与椭圆方程联立,表示出直线AD和BD的方程,联立求得xP,进而知xM,再结合平面向量数量积的坐标运算与韦达定理,化简运算,即可得解.
本题考查直线与椭圆的位置关系,熟练掌握椭圆的方程与几何性质,灵活运用韦达定理是解题的关键,考查逻辑推理能力和运算能力,属于难题.
18.【答案】解:设第一次抽到正常硬币为事件A,抽到双面都印着字的硬币为事件B,抽到双面都印着花的硬币为事件C,
第一次投掷出正面向上为事件M1,第二次投掷出正面向上为事件M2,
选择方案一进行第三次投掷并正面向上为事件M3,选择方案二进行第三次投掷并正面向上为事件N3.
(1)由全概率公式可得P(M1)=P(M1|A)⋅P(A)+P(M1|B)⋅P(B)+P(M1|C)⋅P(C)=12×12+13×1+16×0=712.
(2)连续两次都是正面的概率P(M1M2)=P(M1M2|A)P(A)+P(M1M2|B)P(B)+P(M1M2|C)P(C)
=12×12×12+13×1+16×0=1124.
所以P(A|M1M2)=P(M1M2A)P(M1M2)=P(M1M2|A)P(A)P(M1M2)=12×12×121124=311.
(3)(一)若选择方案一,设第三次投掷后最终获得的礼券为X元,第三次掷出正面向上为事件S,
则P(M3|M1M2)=P(M1M2M3)P(M1M2)
=P(M1M2M3|A)P(A)+P(M1M2M3|B)P(B)+P(M1M2M3|C)P(C)P(M1M2)
=12×12×12×12+13×1+16×01124=1922,
P(S)=1922,1−P(S)=322,
E(X)=1922×200+322×100=410022=205011.
(二)若选择方案二,设第三次投掷后最终获得的礼券为Y元,第三次掷出正面向上为事件T,
①如果第一次抽到的是正常硬币,设第二次抽到正常硬币为事件HA,第二次抽到两面都是字的硬币为事件HB,第二次抽到两面都是花的硬币为事件HC,
则P1=P(M1M2|A)⋅P(A)⋅[P(N3|HA)⋅P(HA)+P(N3|HB)⋅P(HB)+P(N3|HC)⋅P(HC)]
=12×12×12×(25×12+25×1+15×0)=340.
②如果第一次抽到的是两面都是字的硬币,设第二次抽到正常硬币为事件KA,第二次抽到两面都是字的硬币为事件KB,第二次抽到两面都是花的硬币为事件KC,
则P2=P(M1M2|B)⋅P(B)⋅[P(N3|KA)⋅P(KA)+P(N3|KB)⋅P(KB)+P(N3|KC)⋅P(KC)]
=13×1×(35×12+15×1+15×0)=16,
所以P(M1M2M3)=P1+P2=340+16=29120,
P(N3|M1M2)=P(M1M2N3)P(M1M2)=291201124=2955,
P(T)=2955,1−P(T)=2655,
E(Y)=2955×300+2655×100=1130055=226011,
综上,由(一)、(二)可得,E(X)
(2)利用全概率公式和条件概率公式,即可求解;
(3)根据两种不同的方案,结合题意,写出不同的期望,比较后即可判断.
本题主要考查离散型随机变量的期望,概率的求法,考查运算求解能力,属于中档题.
19.【答案】解:(1)当x≤0时,f(x)单调递增,且f(0)=1,x→−∞,f(x)→−∞,
因此f(x)在区间(−∞,0]上存在唯一零点,
当x>0时,只要ex−ax2=0存在两个根即可,即a=exx2存在两个根,
令g(x)=exx2,则g′(x)=(x−2)exx3,
当x∈(0,2)时,g′(x)<0,函数g(x)单调递减;当x∈(2,+∞)时,g′(x)>0,函数g(x)单调递增;
又g(2)=e24,当x→0时,g(x)→+∞;当x→+∞时,g(x)→+∞,
故a>e24时,在区间(0,+∞)存在两个零点,
因此a的取值范围为{a|a>e24};
(2)①f(x)=ex−ax2(a>0),f′(x)=ex−2ax,
令φ(x)=f′(x),则φ′(x)=ex−2a,
x∈(−∞,ln2a)时,φ′(x)<0,f′(x)单调递减,x∈(ln2a,+∞)时,φ′(x)>0,f′(x)单调递增,
令 f′(ln2a)=0,解得a=e2;
②设P(x0,f(x0))为好点,对于任意x∈R,都有(x−x0)⋅[f(x)−g(x)]≥0,
当x=x0时,0≥0成立,
当x>x0时,f(x)−g(x)≥0恒成立,
当x
所以g(x)=f′(x0)(x−x0)+f(x0),
设h(x)=f(x)−g(x),即h(x)=f(x)−f′(x0)(x−x0)−f(x0),
则h′(x)=f′(x)−f′(x0),
又因为f′(x)在(−∞,1)上单调递减,在(1,+∞)上单调递增,
①当x>x0时,因为P为好点,所以h(x)=f(x)−g(x)≥0恒成立,
1∘若x0≥1,f′(x)在(x0,+∞)上单调递增,f′(x)>f′(x0),h′(x)=f′(x)−f′(x0)>0,
所以h(x)在x>x0时单调递增,h(x)>h(x0)=f(x0)−g(x0)=0,满足条件,故x0≥1时成立.
2∘若x0<1,f′(x)在(x0,1)上单调递减,在(1,+∞)上单调递增,在(x0,1)时,f′(x)
所以h(x)在x
2∘若x0>1,f′(x)在(−∞,1)上单调递减,在(1,x0)上单调递增,在(1,x0)时,f′(x)
综上,由①②可得,x0≥1且x0≤1,即x0=1,
所以只有一个好点x0=1.
【解析】(1)由已知判断x≤0时f(x)的单调性,结合函数性质可得f(x)在区间(−∞,0]上存在唯一零点,从而可知,x>0时,ex−ax2=0存在两个根即可,分离参数可得,a=exx2存在两个根,构造函数g(x)=exx2,对g(x)求导,结合函数零点存在条件即可求解;
(2)由已知对函数求导,结合导数的几何意义可求切线方程,然后结合函数极值存在条件及函数的性质即可分别求解.
本题以新定义为载体,主要考查了导数与单调性关系及极值存在条件的应用,还考查了导数与函数性质的综合应用,属于难题.身高x(单位:cm)
167
173
175
177
178
180
181
体重y(单位:kg)
90
54
59
64
67
72
76
2024年江西省抚州市高考数学质检试卷(含详细答案解析): 这是一份2024年江西省抚州市高考数学质检试卷(含详细答案解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2024年山东省泰安市高考数学第一次质检试卷(含详细答案解析): 这是一份2024年山东省泰安市高考数学第一次质检试卷(含详细答案解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2024年吉林省长春市高考数学质检试卷(三)(含详细答案解析): 这是一份2024年吉林省长春市高考数学质检试卷(三)(含详细答案解析),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












