相交线及其所成的角-中考数学二轮知识梳理+专项练习（全国通用）

这是一份相交线及其所成的角-中考数学二轮知识梳理+专项练习（全国通用），共8页。试卷主要包含了 基本概念， 分类， 相交直线所成的角， 特殊位置的角等内容，欢迎下载使用。

知识点
1. 基本概念：相交线指的是在平面上交叉的两条直线，它们交叉于一个点，这个点叫做交点。
2. 分类：
交叉相交线：两条直线在平面上相交形成的交点是线段。
垂直相交线：两条相交的直线之间的夹角为90度。垂直线有一个重要的性质，即垂直线互为相互补角。
平行相交线：两条不相交的直线。
重合相交线：两条直线在平面上完全重合。
3. 相交直线所成的角：当两条直线在同一平面内相交时，它们会形成四个角。
对顶角：相对的两个角称为对顶角。对顶角有一个重要的性质，即它们的角度相等。这意味着，如果∠1与∠2是对顶角，那么∠1=∠2。
邻角：相邻的两个角称为邻角。邻角有一个性质，即它们的角度之和等于180度。这意味着，如果∠3与∠4是邻角，那么∠3+∠4=180°。
4. 特殊位置的角：
同位角：当两条直线被第三条直线所截时，位于这两条直线相同位置的两个角称为同位角。例如，∠1与∠5。
内错角：当两条直线被第三条直线所截时，位于这两条直线之间但位于第三条直线的不同侧的两个角称为内错角。例如，∠3与∠5。
同旁内角：当两条直线被第三条直线所截时，位于这两条直线之间且位于第三条直线的同一侧的两个角称为同旁内角。例如，∠3与∠6。
专项练
一、单选题
1．点P是直线l外一点，A，B，C为直线l上的三点，若，则点P到直线l的距离（ ）
A．小于B．等于C．不大于D．大于
2．如图所示，已知AD平分∠BAE，若∠BAD＝62°，则∠CAE的度数是( )
A．56°B．55°C．58°D．62°
3．下列说法错误的是（ ）
A．同旁内角相等，两直线平行B．内错角相等，两条直线平行
C．对顶角相等D．平行于同一条直线的两条直线平行
4．下列命题是真命题的是（ ）
A．两直线平行，同旁内角相等B．相等的角是对顶角
C．直角三角形的两锐角互余D．三角形的外角大于任一内角
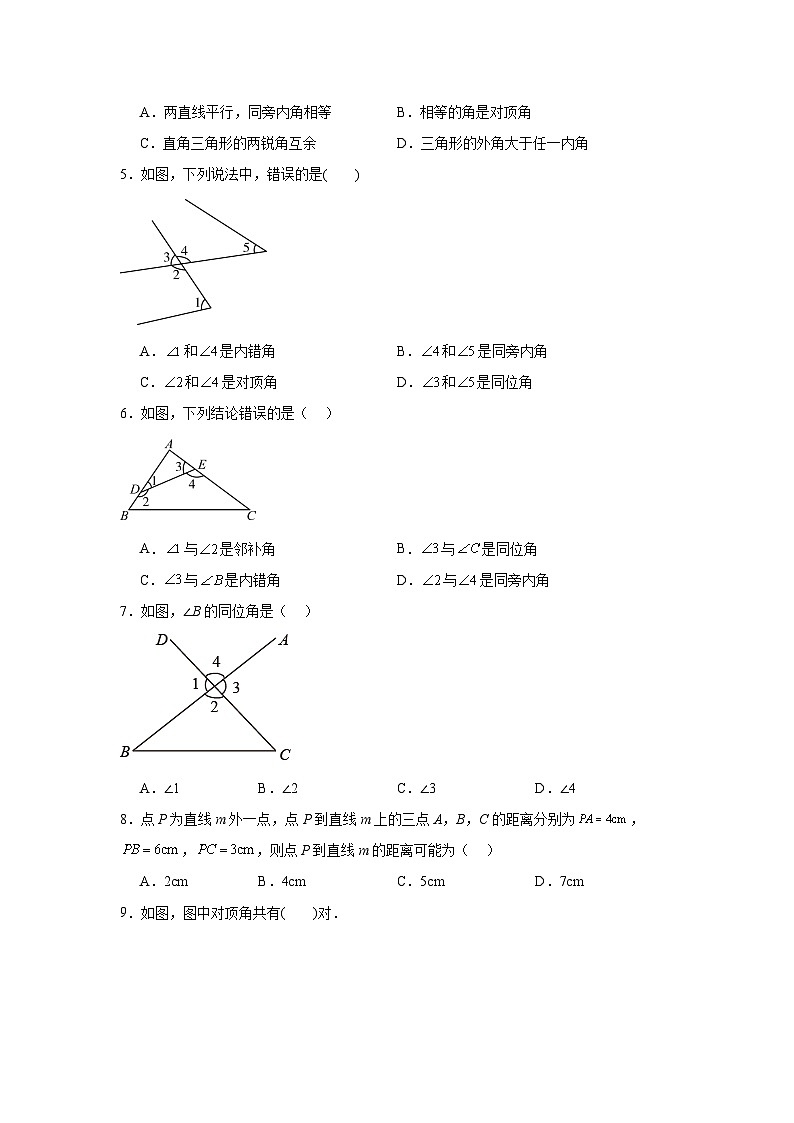
5．如图，下列说法中，错误的是( )
A．和是内错角B．和是同旁内角
C．和是对顶角D．和是同位角
6．如图，下列结论错误的是（ ）
A．与是邻补角B．与是同位角
C．与是内错角D．与是同旁内角
7．如图，∠B的同位角是（ ）
A．∠1B．∠2C．∠3D．∠4
8．点P为直线m外一点，点P到直线m上的三点A，B，C的距离分别为，，，则点P到直线m的距离可能为（ ）
A．2cmB．4cmC．5cmD．7cm
9．如图，图中对顶角共有( )对．
A．6B．11C．12D．13
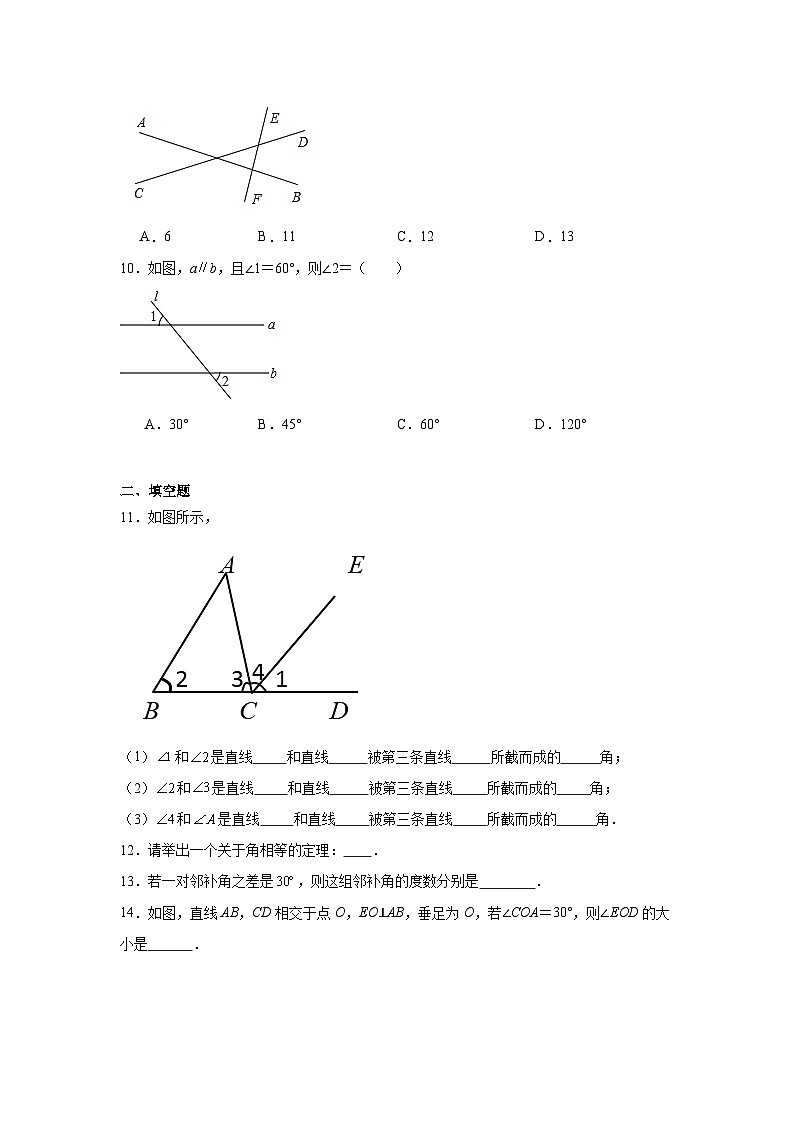
10．如图，ab，且∠1＝60°，则∠2＝（ ）
A．30°B．45°C．60°D．120°
二、填空题
11．如图所示，
（1）和是直线 和直线 被第三条直线 所截而成的 角；
（2）和是直线 和直线 被第三条直线 所截而成的 角；
（3）和是直线 和直线 被第三条直线 所截而成的 角．
12．请举出一个关于角相等的定理： ．
13．若一对邻补角之差是，则这组邻补角的度数分别是 ．
14．如图，直线AB，CD相交于点O，EO⊥AB，垂足为O，若∠COA＝30°，则∠EOD的大小是 ．
15．如图，AB与CD相交于点O，，，则 ．
16．如图，若∠1=60°，那么∠2= ∠3= ∠4= ．

17．如图，长方形纸片，点，分别在边，上，连接，将对折落在直线上的点处，得折痕；将对折，点落在直线上的点得折痕，若，则 ．
18．如图，，分别与交于点P，Q．若，则 °．
19．如图，将一张长方形纸条折叠，若，则 ．
20．如图，已知直线a∥b，∠4=40°，则∠2= .
三、解答题
21．如图，，，分别是，，边上的点，，．
（1）请说明的理由；
（2）若平分，，判断与的位置关系，并说明理由．
22．如图，的顶点，，在边长为的正方形网格的格点（网格线的交点）上，求点到边的距离．

23．如图，在正方形ABCD中，点E是CD边上一动点（点E与点C、D不重合），连接AE，过点A作AE的垂线交CB延长线于点F，连接EF．
(1)依据题意，补全图形；
(2)求∠AEF的度数；
(3)连接AC交EF于点H，若，用含a的等式表示线段CF和CE之间的数量关系，并说明理由．
24．观察如图所示中的各图，寻找对顶角（不含平角）：
（1）如图a，图中共有＿＿＿对对顶角；
（2）如图b，图中共有＿＿＿对对顶角；
（3）如图c，图中共有＿＿＿对对顶角.
（4）研究（1）～（3）小题中直线条数与对顶角的对数之间的关系，若有 n条直线相交于一点, 则可形成＿＿＿对对顶角？
（5）若有2008条直线相交于一点，则可形成＿＿＿对对顶角？
25．如图，已知，，．求证：．
证明：，
__________，（ ）
即__________．
，且，
．
__________，（ ）
∴．（ ）

参考答案：
1．C
2．A
3．A
4．C
5．A
6．C
7．C
8．A
9．A
10．C
11． BA CE BD 同位 BA CA BD 同旁内 BA CE AC 内错
12．两直线平行，同位角相等
13．，
14．120°
15．/90度
16． 120° 60° 120°
17．
18．
19．76°
20．140°
21．（1）略；（2）CD⊥EG
22．
23．(1)略
(2)∠AEF=45°
(3)数量关系为CF=aCE
24．（1）2；（2）6；（3）12；（4）n（n-1）；（5）4030056
25．；垂直的定义；；；同角的余角相等；同位角相等，两直线平行