




山东省聊城市莘县2023-2024学年七年级下学期期中数学试题(原卷版+解析版)
展开(时间:120分钟;满分:120分)
一、选择题:(本题共10个小题,每小题3分,共30分,每小题只有一个选项符合题目要求)
1. 下列方程:①,②,③,④,⑤是二元一次方程的有( )
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
【分析】本题主要考查二元一次方程的概念,二元一次方程满足的条件:为整式方程,只含有2个未知数,未知数的最高次数是1,据此进行判断即可
【详解】解:①符合二元一次方程的定义,故①是二元一次方程;
②不是整式方程,不符合二元一次方程的定义,故②不是二元一次方程;
③含有3个未知数,不符合二元一次方程的定义,故③不是二元一次方程;
④不是等式,不符合二元一次方程的定义,故④不是二元一次方程;
⑤符合二元一次方程的定义,故⑤是二元一次方程;
故是二元一次方程是①⑤,共2个,
故选:B
2. 数学课上老师用双手形象表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A. 同旁内角、同位角、内错角
B. 同位角、内错角、对顶角
C. 对顶角、同位角、同旁内角
D. 同位角、内错角、同旁内角
【答案】D
【解析】
【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.
【详解】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
【点睛】本题考查了同位角、内错角、同旁内角,解题的关键是掌握同位角、内错角、同旁内角,并能区别它们.
3. 我国在大力实施德智体美全面发展的素质教育,为进一步增强体育训练,学校对跳远项目进行测试,这是王洋同学跳落沙坑时留下的痕迹,则表示王洋成绩的是( )
A. 线段的B. 线段的长
C. 线段的长D. 线段的长
【答案】B
【解析】
【分析】本题考查垂线段的特点,解题关键是掌握直线外一点到直线的距离的定义,即直线外任意一点到这条直线的垂线段的长度,叫做点到这条直线的距离.根据直线外一点到直线的距离的定义,结合跳远比赛的规则,即可求解.
【详解】解:跳远成绩应该为身体与沙坑的接触点中到踏板的垂线段长的最小值,
表示王洋成绩的是线段的长,
故选:B.
4. 下列运算正确的是
A. B.
C. D.
【答案】C
【解析】
【分析】本题主要考查整式的运算,根据单项式乘多项式、合并同类项、积的乘方和幂的乘方运算法则计算出各项后再判断即可
【详解】解:A. ,故选项A计算错误,不符合题意;
B. ,故选项B计算错误,不符合题意;
C. ,故选项C计算正确,符合题意;
D. ,故选项D计算错误,不符合题意;
故选:C
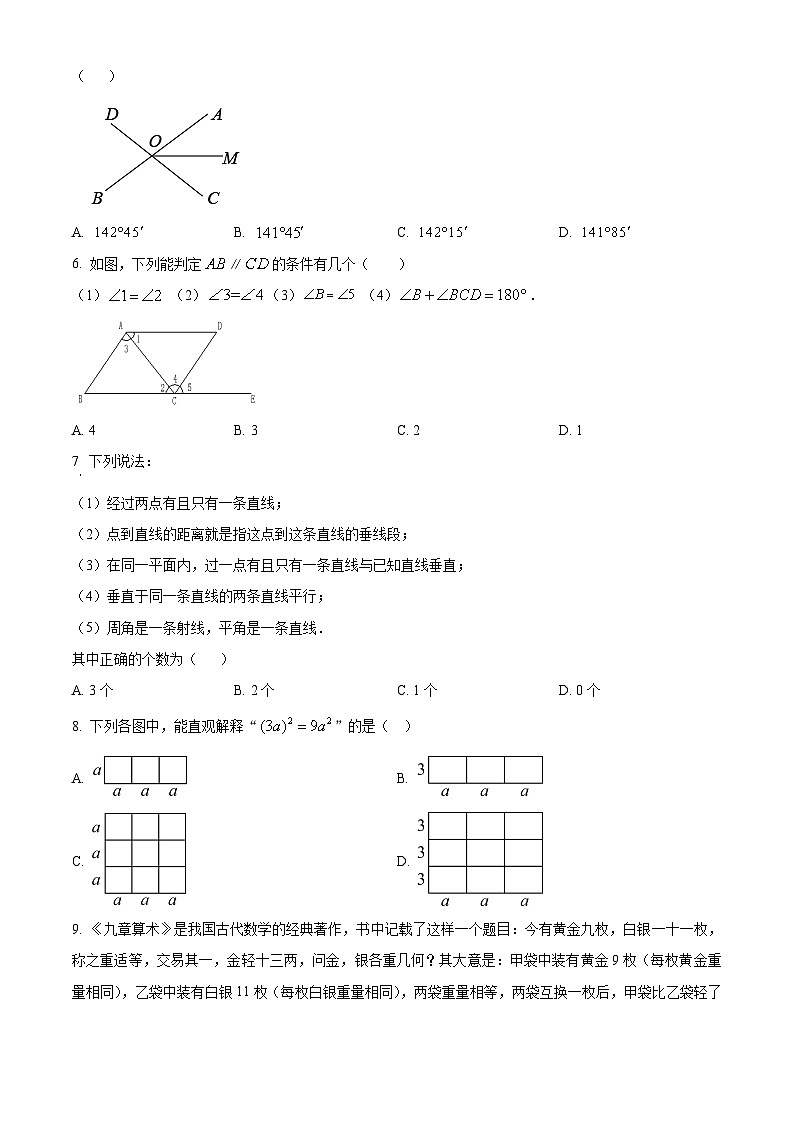
5. 如图,直线,交于点O,射线平分,若,则等于( )
A. B. C. D.
【答案】B
【解析】
【分析】根据角平分线的定义求出∠AOM的度数,然后根据平角等于180°列式计算即可得解.
【详解】解:∵,
射线OM平分∠AOC,
∴,
∴.
故选:B.
【点睛】本题考查了邻补角、角平分线的定义,准确运用角的和差关系进行计算是解题的关键.
6. 如图,下列能判定∥的条件有几个( )
(1) (2)(3) (4).
A. 4B. 3C. 2D. 1
【答案】B
【解析】
【分析】根据平行线的判定逐一判定即可.
【详解】因为,所有AD∥BC,故(1)错误.
因为,所以∥,故(2)正确.
因,所以∥,故(3)正确.
因为,所以∥,故(4)正确.
所以共有3个正确条件.
故选B
【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.
7. 下列说法:
(1)经过两点有且只有一条直线;
(2)点到直线的距离就是指这点到这条直线的垂线段;
(3)在同一平面内,过一点有且只有一条直线与已知直线垂直;
(4)垂直于同一条直线的两条直线平行;
(5)周角是一条射线,平角是一条直线.
其中正确的个数为( )
A. 3个B. 2个C. 1个D. 0个
【答案】B
【解析】
【分析】利用平行公理以及其推论和垂线的定义、特殊角、点到直线的距离的定义分别分析求出即可.
【详解】解:(1)经过两点有且只有一条直线,说法正确;
(2)点到这条直线的垂线段的长度才是点到直线的距离,故(2)说法错误;
(3)在同一平面内,过一点有且只有一条直线与已知直线垂直,说法正确;
(4)垂直于同一条直线的两条直线平行,要强调在同一平面内,故(4)说法错误;
(5)角是由一个公共端点发出的两条射线组成,即便两射线所在的直线重合,也不能认为是一条射线或直线,故(5)错误.
故选:B
【点睛】此题主要考查了平行公理以及其推论和垂线的定义、点到直线的距离的定义等,正确把
握相关定义是解题关键.
8. 下列各图中,能直观解释“”的是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据长方形和正方形的面积计算公式进行求解即可.
【详解】、 表示,故不符合题意;
B、 表示,故不符合题意;
C、 表示,故符合题意;
D、 表示,故不符合题意.
故选:C.
【点睛】本题主要考查了积的乘方计算,正确理解数形结合的思想求解是解题的关键.
9. 《九章算术》是我国古代数学的经典著作,书中记载了这样一个题目:今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金,银各重几何?其大意是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),两袋重量相等,两袋互换一枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金,白银各重几两?设每枚黄金重x两,每枚白银重y两,根据题意得方程组( )
A. B.
C D.
【答案】B
【解析】
【分析】本题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系:①枚黄金的重量11枚白银的重量;②枚白银的重量枚黄金的重量1枚白银的重量枚黄金的重量两.
【详解】解:设每枚黄金重x两,每枚白银重y两,根据题意得方程组为,
故选:B.
10. 实践活动课上,老师展示了如图1是的一张纸条,按图1→图2→图3,把这一纸条先沿折叠并压平,再沿折叠并压平,若图3中,则图2中的度数为( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决本题的关键是画出折叠前后的图形.设,根据折叠的性质得,则,再由第2次折叠得到,于是利用平角定义可计算出,接着根据平行线的性质得,据此即可求得.
【详解】解:如图,设,
∵纸条沿折叠,
∴,
∴,
∵纸条沿折叠,
∴,
而,
∴,
解得,
∵,
∴,
∴.
故选:A.
二、填空题:(本题共6小题,每小题3分,共18分)
11. 清代诗人袁枚创作了一首诗《苔》:“白日不到处,青春恰自来.苔花如米小,也学牡丹开”歌颂了苔在恶劣环境下仍有自己的生命意向.若苔花的花粉粒直径约为米,用科学记数法表示,则______.
【答案】
【解析】
【分析】本题考查用科学记数法表示较小的数,一般形式为,其中,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】解:用科学记数法表示为,
∴.
故答案为:.
12. 已知,,则______.
【答案】9
【解析】
【分析】本题主要考查同底数幂的除法和幂的乘方的逆用,即 , ,解答的关键是灵活应用同底数幂的除法和幂的乘方的逆用运算.利用同底数幂的除法的法则及幂的乘方的法则对式子进行变形整理,再代入相应的值运算即可.
【详解】解:∵,,
∴
.
故答案为:9.
13. 已知的乘积中不含项和项,则______.
【答案】
【解析】
【分析】本题考查多项式的乘法中不含某些项,掌握不含某些项就是某些项的系数为零是解题的关键.按照多项式乘以多项式展开合并后,不含项和项,则这些项的系数为零解题即可.
【详解】解:
,
∵结果中不含项和项,
∴,
解得,
∴,
故答案为:.
14. 生活中常见一种折叠拦道闸,若想求解某些特殊状态下的角度,需抽象为几何图形,如图,垂直于地面于A,平行于地面,则______.
【答案】##270度
【解析】
【分析】过点B作,如图,由于,则,根据两直线平行,同旁内角互补得,由得,即,于是得到结论.
本题主要考查了平行线的性质,正确作出辅助线,并熟记两直线平行,同旁内角互补是解决问题的关键.
【详解】解:过点B作,如图,
∵,
∴,
∴,
∵,
∴,
∴,
.
故答案为:.
15. 一般地,n个相同因数a相乘:记为.如,此时,指数3叫做n个以2为底的8的对数,记为,(即).请运算______.
【答案】20
【解析】
【分析】本题考查了有理数的乘方,根据乘方运算可得对数的答案根据有理数的加法运算可得答案.
【详解】解:∵,
∴,
∴,
∵,
∴,
∴,
故答案为:20.
16. 如图,在已知一个角内部画射线,画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角;求画10条射线得的角共有______个
【答案】66
【解析】
【分析】本题考查了对角的概念和规律探索,根据画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角,可以得出规律是画n条射线,图中共有 个角,把代入计算即可.
【详解】解:∵在已知角内画射线,画1条射线,图中共有3个角,;
画2条射线,图中共有6个角,;
画3条射线,图中共有10个角,;
…,
∴画n条射线,图中共有个角,
∴画10条射线所得的角的个数是(个),
故答案为:66.
三、解答题(本题共8个小题,共72分,解答应写出文字说明、证明过程或演算步骤).
17. (1)计算:
(2)化简求值:,其中,
【答案】(1);(2);
【解析】
【分析】本题主要考查整式的运算和化简求值:
(1)原式先计算同底数幂的乘除法和积的乘方与幂的乘方,然后再合并即可得出答案 ;
(2)先根据多项式乘以多项式,平方差公式将括号去掉,再合并得最简结果,再计算出的值,代入计算即可.
【详解】解:(1)
;
(2)
,
又,,
所以,把,代入,原式
18. 解下列方程组:
(1)
(2)
【答案】(1)
(2)
【解析】
【分析】本题主要考查解二元一次方程组:
(1)求出,再把代入①得求出y的值即可得出方程组的解;
(2)由得,由求得,把代入②求出y的值即可得出方程组的解
【小问1详解】
解:
由得,,
解得,
把代入①得,,
解得
所以;
【小问2详解】
解:
由,得,
由,得,
解得,
把代入②得,,
解得,
所以
19. 如图,,垂足为是上任意一点,,垂足为,且,.
(1)求证:
(2)求的度数
【答案】(1)见解析(2)80°
【解析】
【分析】(1)先根据CD⊥AB于D,FE⊥AB得出CD∥EF,故可得出∠2=∠DCB,根据∠2=∠DCB,∠1=∠2得出DG∥BC,由此可得出结论;
(2)根据DG∥BC即可得出结论.
【详解】(1)∵CD⊥AB,FE⊥AB,
∴CD∥EF
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD
∴BC∥DG,
(2)∵DG∥BC,
∴∠3=∠BCG,
∵∠3=80°,
∴∠BCA=80°.
【点睛】本题考查的是平行线的判定与性质,解题时注意:内错角相等,两直线平行.
20. 如图,若,与、分别相交于E、F,,的平分线与相交于点P,且,求的度数.
【答案】
【解析】
【分析】本题主要考查了平行线的性质,垂线定义理解,角平分线的定义,根据垂线定义得出,,求出,根据平行线的性质求出,根据角平分线定义得出,即可得出答案.
【详解】解:∵,
,,
,
,
,
,
平分,
,
.
21. 阅读下列材料:为了提高全县学生的运算能力和解题技巧,李老师设计了如下的题目:
解方程,王栋同学发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的看作一个数,把看作一个数,通过换元,可以解决问题.下面是他的解题过程:令,,这时方程组可化为解得,把代入,得,解得,
(1)在解二元一次方程组时,我们的基本思路是“消元”,即通过“代入法”或“加减法”将“二元”化为“一元”,在“消元”的过程体现的数学思想是( )
A.数形结合思想 B.转化思想 C.分类讨论思想 D.类比思想
(2)请你参考王栋同学的做法,解决下面的问题:解方程组
【答案】(1)
(2)
【解析】
【分析】本题考查了解二元一次方程组,整体代入法求解:
(1)在解二元一次方程组时,我们的基本思路是“消元”,即通过“代入法”或“加减法”将“二元”化为“一元”,在“消元”的过程体现的数学思想是转化思想;
(2)结合题意,利用整体代入法求解,令,,方程组化为,再运用加减消元法求解即可
【小问1详解】
解:在解二元一次方程组时,我们的基本思路是“消元”,即通过“代入法”或“加减法”将“二元”化为“一元”,在“消元”的过程体现的数学思想是转化思想,
故选:B;
【小问2详解】
解:令,,方程组化为,
得:,即,
将代入①得:,
将,代入得:,
解得:
22. 已知,射线在的内部,按要求完成下列各小题.
(1)尝试探究:如图1,已知,的度数为________;
(2)初步应用:如图2,若时,求的度数,并说明理由;
(3)拓展提升:如图3,若,试判断与之间数量关系,并说明理由.
【答案】(1)
(2),理由见解析
(3)
【解析】
【分析】本题考查了角的和差,掌握角度之间的关系是解决本题的关键.
(1)首先根据题意得到,然后利用角的和差求解即可;
(2)首先根据题意得到,然后利用角的和差求解即可;
(3)首先根据题意得到,然后利用角的和差求解即可
【小问1详解】
∵
∴;
【小问2详解】
∵
∴;
小问3详解】
∵
∴;
23. 2024“全民健身活力中国”汉方普惠杯——聊城莘县赛区海选,参赛者为了购买服装,在某商厦购买商品,共三次,只有一次购买时,商品,同时打折,其余两次均按标价购买,三次购买商品,的数量和费用如下表:
(1)参赛者按打折扣价购买商品A,是第______次购买;
(2)求商品A,的标价;
(3)若商品A,的折扣相同,则商店是打几折出售这两种商品的?
【答案】(1)三 (2)商品A的标价为90元/个,商品的标价为120元/个
(3)商店是打6折出售这两种商品的.
【解析】
【分析】本题考查了一元一次方程的应用,二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.
(1)根据图表可得第三次购物花的钱最少,买到A、B商品又是最多,所以以折扣价购买商品A、B是第三次购物;
(2)设商品A的标价为x元/个,商品B的标价为y元/个,列出方程组求出x和y的值;
(3)设商店是打a折出售这两种商品,根据打折之后购买9个A商品和8个B商品共花费1062元,列出方程求解即可.
【小问1详解】
解:参赛者按打折扣价购买商品A,是第三次购买;
【小问2详解】
解:设商品A的标价为元/个,商品的标价为元/个,
根据题意得:,
解得,
经检验,方程组的解符合题意.
答:商品A的标价为90元/个,商品的标价为120元/个;
【小问3详解】
解:设商店是打折出售这两种商品的,
由题意得,
解得,
答:商店是打6折出售这两种商品的.
24. 数学活动——探究日历中的数字规律
如图1是2024年3月份的日历,张亮在其中画出两个的方框,每个框均框住位置为的四个数,张亮准备:计算“”的值,探索其运算结果的规律.
(1)计算:______;
(2)张亮通过特例分析,猜想所有日历中,方框里“”的结果都不变,并说明理由如下,请你将其过程补充完整;
解:的值均为______.理由如下:
设,则,,______,
因为______,
所以的值均为______.
(3)同学们利用张亮的方法,借助2024年4月份的日历,继续进行如下探究.
请从下列A,B两题中任选一题作答.我选择______.
A.如图2,在日历中用“十字框”框住位置为的五个数,探究“”的值的规律,写出你的结论,并说明理由.
B.在日历中用“H型框”框住位置为的七个数,探究“”的值的规律,写出你的结论,并说明理由.
【答案】(1)7 (2)7;;7;7
(3)若选A.,理由见解析;若选B.,理由见解析
【解析】
【分析】(1)根据有理数混合运算的法则计算求解;
(2)代入化简求值即可;
(3)A:结论:,设中间#为,则,,,,列式计算可得结果;
B:结论:.设中间#为,则,,,,,,列式计算可得结果.
【小问1详解】
解:;
【小问2详解】
解:的值均为7,理由如下:
设,则,,,
因为
,
所以的值均为7.
故答案为:7;;7;7.
【小问3详解】
同学们利用张亮的方法,借助2024年4月份的日历,继续进行如下探究.
请从下列,两题中任选一题作答,我选择或
在日历中用“十字框”框住位置为
结论:
理由设中间#为,则,,,,
;
B.在日历中用“型框”框住位置为
结论:
理由:设中间#为,则,,,,,,
.
【点睛】本题考查了日历中的数字问题,有理数的混合运算,整式的加减等知识,解题的关键是学会模仿例题解决问题.购买商品的数量(个)
购买商品的数量(个)
购买总费用(元)
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
山东省聊城市莘县2023-2024学年七年级下学期4月期中数学试题: 这是一份山东省聊城市莘县2023-2024学年七年级下学期4月期中数学试题,共4页。
山东省聊城市莘县2023—-2024学年九年级下学期期中数学试题: 这是一份山东省聊城市莘县2023—-2024学年九年级下学期期中数学试题,共6页。
山东省聊城市莘县春笋学校2023-2024学年八年级下学期3月月考数学试题(原卷版+解析版): 这是一份山东省聊城市莘县春笋学校2023-2024学年八年级下学期3月月考数学试题(原卷版+解析版),文件包含精品解析山东省聊城市莘县春笋学校2023-2024学年八年级下学期3月月考数学试题原卷版docx、精品解析山东省聊城市莘县春笋学校2023-2024学年八年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。












