



山东省淄博市高青县第一中学2023-2024学年高一下学期期中考试数学试题(原卷版+解析版)
展开注意事项:
1.本试题分第I卷和第I卷两部分.第I卷为选择题,共58分;第II卷为非选择题,共92分;满分150分,考试时间为120分钟.
2.客观题请将选出的答案标号(A、B、C、D)涂在答题卡上,主观题用黑色签字笔答题.
第I卷(共58分)
一、单选题(本题共8小题,每小题5分,共40分)
1. 在中,已知,,,则( )
A. 1B. C. D. 3
2. 若,则( )
A B. C. D.
3. 在中,已知,,且的面积为3,则A=( )
A B. C. 或D. 或
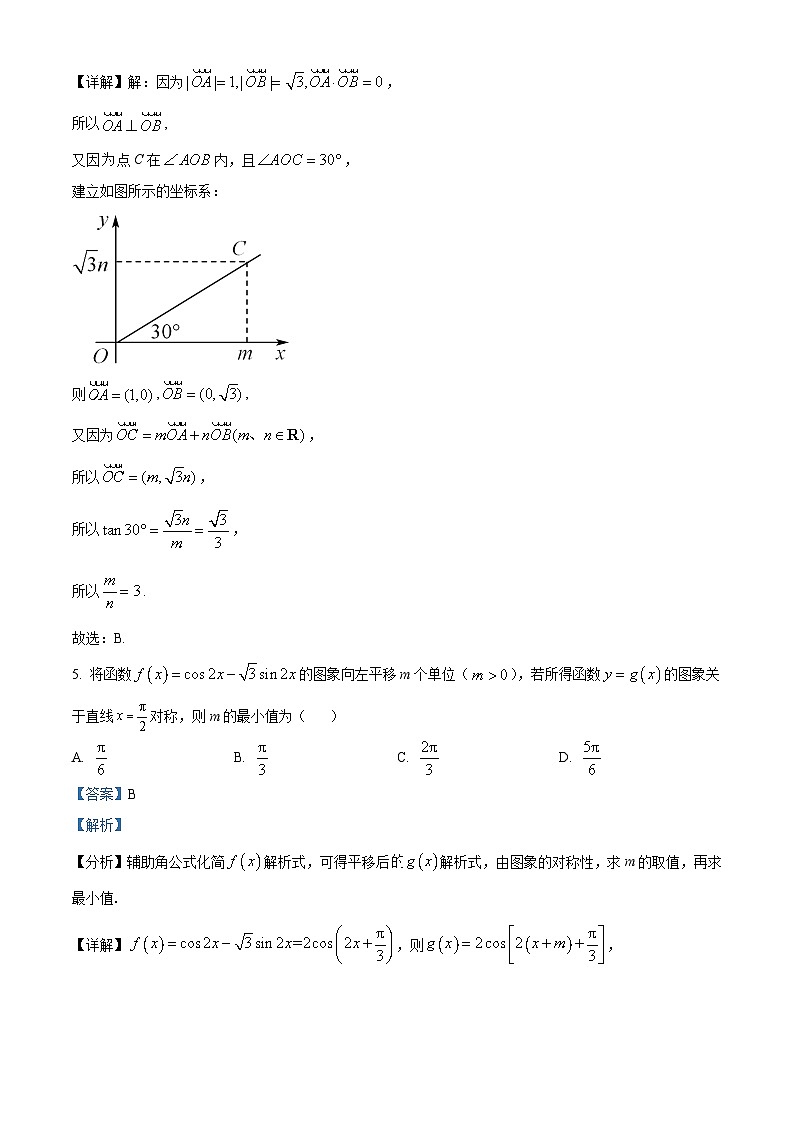
4. 已知,点C在内,且.设,则等于( )
A. B. 3C. D.
5. 将函数的图象向左平移m个单位(),若所得函数的图象关于直线对称,则m的最小值为( )
A. B. C. D.
6. 已知向量,,,,若在上的投影向量为(是与同向的单位向量),则( )
A. 169B. 13C. 196D. 14
7. 已知,则( ).
A. B. C. D.
8. 如图所示,为线段外一点,若中任意相邻两点间的距离相等,,则用表示,其结果为( )
A. B. C. D.
二、多选题(本题共3小题,共18分.在每小题给出的选项中,由多项符合题目要求)
9. 计算下列各式,结果为的是( )
A. B.
C. D.
10. 已知a,b,c分别是三个内角A,B,C的对边,则下列命题中错误的是( )
A. 若是锐角三角形,则
B. 若是边长为1的正三角形,则
C. 若,,,则有一解
D. 若,则是等腰直角三角形
11. 下列说法正确的是( )
A. 设是两个不共线的向量,若向量与向量共线,则
B. 在中,若,则
C. 设,且,则
D. 若是内一点,满足,则
第II卷(共92分)
三、填空题(本题共3小题,每小题5分,共15分)
12. 已知向量满足,且,则与夹角为_________.
13. 已知,则 ________.
14. 如图所示,某摩天轮设施,其旋转半径为50米,最高点距离地面110米,开启后按逆时针方向匀速旋转,转一周大约21分钟.某人在最低点的位置坐上摩天轮座舱,并开始计时,则第7分钟时他距离地面的高度大约为________米.
四、解答题
15. 已知函数
(1)求的单调递增区间及最小正周期;
(2)若,且,求.
16. 已知向量,.
(1)若,求的值;
(2)若,与夹角为锐角,求实数m的取值范围.
17. 如图,A、B是海面上位于东西方向相距海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距海里的C点的救援船立即前往营救,其航行速度为30海里/小时,试求:
(1)轮船D与观测点B的距离;
(2)救援船到达D点所需要的时间.
18. 在中,角,,的对边分别为,,,.
(1)求;
(2)若点是上的点,平分,且,求面积的最小值.
19. “费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:已知的内角所对的边分别为,且
(1)求;
(2)若,设点为的费马点,求;
(3)设点为的费马点,,求实数的最小值.
上海市延安中学2023-2024学年高一下学期期中考试数学试题(原卷版+解析版): 这是一份上海市延安中学2023-2024学年高一下学期期中考试数学试题(原卷版+解析版),文件包含上海市延安中学2023-2024学年高一下学期期中考试数学试题原卷版docx、上海市延安中学2023-2024学年高一下学期期中考试数学试题解析版docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
山东省淄博市高青县第一中学2023-2024学年高一下学期期中考试数学试题: 这是一份山东省淄博市高青县第一中学2023-2024学年高一下学期期中考试数学试题,共7页。试卷主要包含了本试题分第I卷和第I卷两部分,在中,已知,且的面积为3,则,已知,点在内,且,已知向量,若在上的投影向量为,已知,则),计算下列各式,结果为的是,等内容,欢迎下载使用。
山东省淄博市高青县第一中学2023-2024学年高二下学期期中学分认定考试数学试题: 这是一份山东省淄博市高青县第一中学2023-2024学年高二下学期期中学分认定考试数学试题,文件包含山东省淄博市高青县第一中学2023-2024学年高二下学期期中考试数学试题pdf、高二数学答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。












